Теорема о перемножении шансов

Пусть одно действие можно проделать пятью способами, а другое — двумя. Каким числом способов можно проделать пару этих действий?

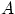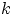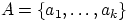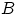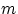Теорема 1. Пусть множество состоит из элементов: , а множество — из элементов: 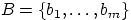. Тогда можно образовать ровно 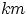пар 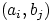, взяв первый элемент из множества 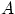, а второй — из множества .

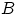Замечание 1. Можно сформулировать утверждение теоремы 1 так: если первый элемент можно выбрать 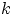способами, а второй элемент — 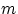способами, то пару элементов можно выбрать 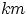способами.

Доказательство. С элементом 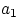мы можем образовать 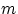пар: 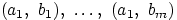. Столько же пар можно составить с элементом 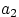, столько же — с элементом 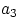и с любым другим из 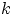элементов множества 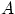. Т.е. всего возможно 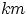пар, в которых первый элемент выбран из множества 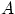, а второй — из множества .

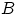QED

Упражнение 1. С помощью теоремы 1 доказать, что:

а)

при подбрасывании трёх монет возможно 2·2·2=8 различных результатов;

б)

бросая дважды игральную кость, получим 6·6=36 различных результатов;

в)

трёхзначных чисел бывает 9·10·10=900;

г)

трёхзначных чисел, все цифры которых различны, существует 9·9·8;

д)

чётных трёхзначных чисел возможно 9·10·5.

Date: 2015-07-02; view: 762; Нарушение авторских прав