Свойства сопряженных чисел

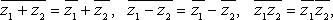
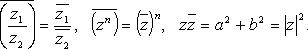
Свойства модуля

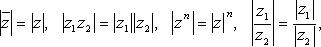
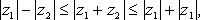
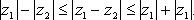
Свойства аргумента

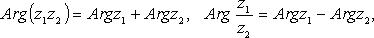
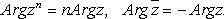
Показательная (экспоненциальная) форма комплексных чисел

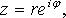
где r - модуль; 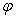- аргумент;

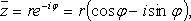
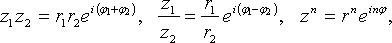
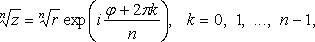
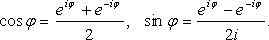
Уравнение переменного напряжения имеет вид 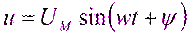, где u – мгновенное значение напряжения; 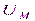– максимальное значение (амплитуда) напряжения; w – угловая частота; t – время; 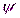– начальный фазовый угол; 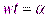– электрический угол. Это уравнение связывает две переменные величины: напряжение u и время t. С течением времени напряжение изменяется синусоидально.

Аналогичный вид имеют уравнения и других синусоидально изменяющихся величин: тока 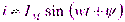, э.д.с. 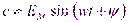и т.д.

При расчете цепей переменного тока приходится использовать синусоидально изменяющиеся величины, т.е. производить сложение, вычитание, умножение и деление уравнений указанного выше типа.

Сложение синусоидальных величин трудоемко, особенно если приходится складывать большое число уравнений. Синусоидальная величина однозначно представлена вращающимся вектором, длина которого равна амплитуде, а начальное положение определяется углом 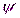, вращение вектора происходит с угловой скоростью w. Операции производятся с уравнениями, имеющими одинаковую угловую частоту, то есть все векторы, заменяющие уравнения, вращаются с одинаковой угловой скоростью. Следовательно, их взаимное расположение не меняется, отпадает необходимость вращения векторов. Так как векторы заменяют синусоидальные величины, то сложение или вычитание, возможно, заменить сложением или вычитанием векторов.

Переменная синусоидальная величина обладает свойствами:

1. Переменная синусоидальная величина может быть однозначно представлена вектором. Длина вектора равна амплитуде; угол наклона равен начальному фазовому углу.

2. Сложение (и вычитание) синусоидальных величин можно заменить сложением (и вычитанием) векторов.

Кроме сложения и вычитания синусоидальные величины приходится умножать и делить. И здесь на помощь приходят комплексные числа.

Комплексное число может быть изображено на плоскости вектором, длина которого равна модулю комплексного числа, а угол наклона – аргументу. В электротехнике в отличие от математики мнимая единица обозначается буквой j. Если имеется комплексное число A=a+jb, то его можно представить вектором, где 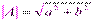– модуль комплексного числа; 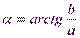– аргумент комплексного числа.

Комплексное число имеет три формы: алгебраическую – A=a+jb; тригонометрическую – 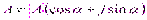; показательную – .

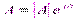Комплексное число однозначно представлено вектором, а определенному вектору соответствует определенное комплексное число.

Таким образом, если переменная синусоидальная величина может быть представлена вектором, а определенному вектору соответствует определенное комплексное число, то переменная синусоидальная величина может быть представлена комплексным числом. Такие величины как: напряжение и ток, сопротивление и проводимость, мощность выражаются комплексными числами.

Напряжение и ток. Имеется уравнение . В электротехнике за длину вектора берется не максимальное, а действующее значение. Оно обозначается большой буквой U без индекса и вычисляется путем деления максимального 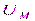значения на .

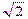Синусоидальная величина, выраженная комплексным числом, называется комплексом и обозначается прописной буквой с точкой наверху 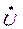. Комплекс напряжения можно написать в трех формах алгебраической – 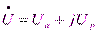, тригонометрической – 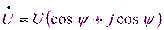и показательной – .

Таким образом, в комплексе напряжения модуль равен действующему значению, аргумент – начальному фазовому углу, активная составляющая – вещественной части комплекса напряжения, реактивная – мнимой части.

Аналогично для тока: _{, , , , .}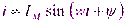

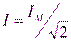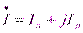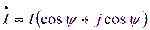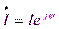Пример. Дано: ток в комплексной форме 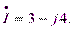Написать уравнение тока.

Решение. Для того чтобы написать уравнение, надо знать амплитуду и начальный фазовый угол. Поэтому надо найти модуль – действующее значение и аргумент – начальный фазовый угол заданного комплекса тока:

, , ,

.

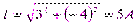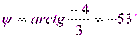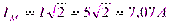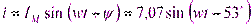Сопротивление и проводимость. Имеется цепь (рис. 1): r – активное сопротивление (лампа накаливания); 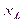– индуктивное сопротивление (катушка); z – общее сопротивление цепи, называемое полным.

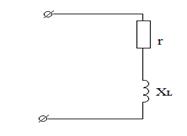
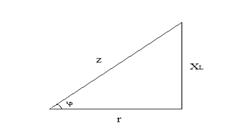
Рис.1 Рис.2

Сопротивления r, 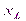, z образуют прямоугольный треугольник сопротивления (рис. 2). Угол 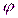– угол сдвига фаз. Сопротивления не являются синусоидальными величинами, однако отрезок z может быть выражен комплексным числом, считая, что отрезок r откладывается по оси вещественных чисел, а отрезок 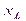– по оси мнимых чисел.

Сопротивление в комплексной форме обозначается буквой Z. Для цепи на рис.2 комплекс сопротивления записывается: – алгебраическая форма; 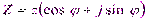– тригонометрическая форма; 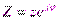– показательная форма.

Модуль 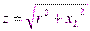; аргумент 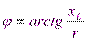. Таким образом, в комплексе сопротивления модуль равен полному сопротивлению, а аргумент – сдвигу фаз.

Мощность. Комплекс мощности получится, если комплекс напряжения умножить на сопряженный комплекс тока: 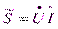, где 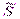– комплекс мощности, – сопряженный комплекс тока.

После умножения получим комплексное число, у которого вещественная часть равна активной мощности, а мнимая часть – реактивной мощности:

, где P – активная мощность, Q – реактивная мощность.

Пример. 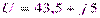,6; 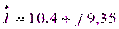. Определить активную P и реактивную Q мощность.

Решение. Переведем комплексы напряжения и тока в показательную форму, для этого найдем модуль и аргумент тока и напряжения:

, , ,

, , .

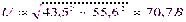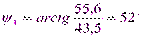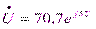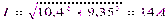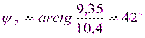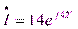Определим сопряженный комплекс тока: ,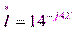

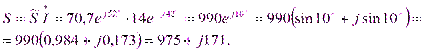
Найдем активную и реактивную мощности: P=975Вт, Q=171 вар.

Алгебраическая форма комплексного числа удобна при сложении и вычитании, показательная – при умножении и делении; тригонометрическая служит для перевода показательной формы в алгебраическую.

_________________________________________________________________

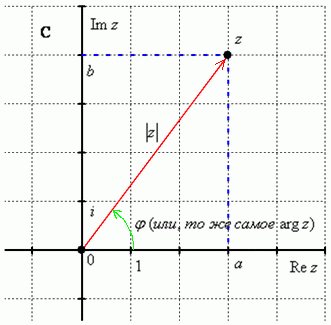
Модулем комплексного числа 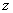называется расстояние от начала координат до соответствующей точки комплексной плоскости. Попросту говоря, модуль – это длина радиус-вектора, который на чертеже обозначен красным цветом.

Модуль комплексного числа 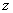стандартно обозначают: 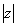или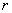

По теореме Пифагора легко вывести формулу для нахождения модуля комплексного числа:

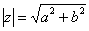. Данная формула справедлива для любых значений «а» и «бэ».

Аргументом комплексного числа 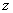называется угол 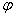между положительной полуосью действительной оси 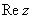и радиус-вектором, проведенным из начала координат к соответствующей точке. Аргумент не определён для единственного числа: .

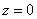Аргумент комплексного числа 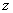стандартно обозначают: 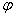или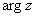

Из геометрических соображений получается следующая формула для нахождения аргумента:
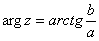. Внимание! Данная формула работает только в правой полуплоскости! Если комплексное число располагается не в 1-ой и не 4-ой координатной четверти, то формула будет немного другой. Эти случаи мы тоже разберем.

В оформлении простейших примеров так и следует записывать: «очевидно, что модуль равен… очевидно, что аргумент равен...». Это действительно очевидно и легко решается устно.

Перейдем к рассмотрению более распространенных случаев. Как я уже отмечал, с модулем проблем не возникает, всегда следует использовать формулу 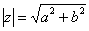. А вот формулы для нахождения аргумента будут разными, это зависит от того, в какой координатной четверти лежит число 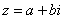. При этом возможны три варианта (их полезно переписать к себе в тетрадь):

1) Если (1-ая и 4-ая координатные четверти, или правая полуплоскость), то аргумент нужно находить по формуле .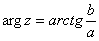

2) Если (2-ая координатная четверть), то аргумент нужно находить по формуле .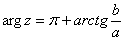

3) Если 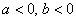(3-я координатная четверть), то аргумент нужно находить по формуле .

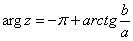Наконец-то. Меня всю дорогу подмывало привести этот маленький примерчик:

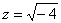
Нельзя извлечь корень? Если речь идет о действительных числах, то действительно нельзя. В комплексных числах извлечь корень – можно! А точнее, два корня:

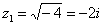
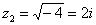
Действительно ли найденные корни являются решением уравнения 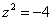? Выполним проверку:

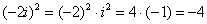
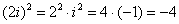
Что и требовалось проверить.

Часто используется сокращенная запись, оба корня записывают в одну строчку под «одной гребёнкой»: .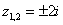

Такие корни также называют сопряженными комплексными корнями.

Date: 2015-07-02; view: 727; Нарушение авторских прав