Достаточные условия существования конечного предела функции

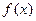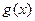Теорема (об арифметике). Если для и существуют конечные пределы, то для их суммы и произведения также существуют конечные пределы, причем:

;

.

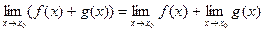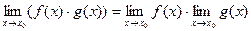Если 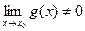, то существует конечный предел частного:

.

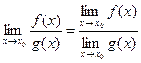Док-во. Докажем, например, второе равенство.

Пусть существуют конечные пределы 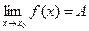и . Докажем, что существует конечный предел .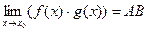

Итак, мы должны доказать, что:

.

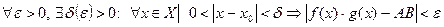Возьмем произвольное 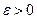. Найдем 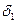из условия 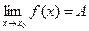, т.е. для этого : .

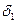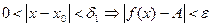Найдем 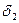из условия , т.е. для этого :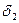

.

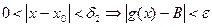Т.к. для 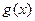по условию существует конечный предел в т. 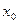, то эта функция будет ограниченной в некоторой окрестности т. 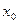(по теореме о локальной ограниченности), т.е. 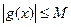- некоторой константы.

Положим 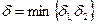. Проверим, что это 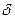- искомое. Действительно,

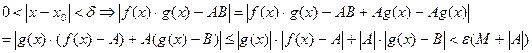
В силу произвольности 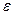можно считать утверждение доказанным (или можно было искать 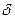не по 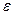, а по ). ▲

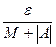Теорема (о промежуточной функции). Пусть для функци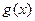й и 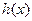существуют конечные пределы в т. 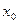, равные друг другу, и в некоторой окрестности т. 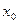, за исключением самой этой точки, выполняется условие:

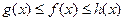. Тогда для 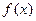тоже существует конечный предел в т. 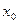, равный значению пределов функци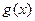й и .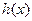

Теорема (о пределе монотонной ограниченной функции). Если функция монотонно возрастает (убывает) в некоторой окрестности т. 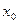и ограничена сверху (снизу), то она имеет в этой точке соответствующий односторонний предел.

Вычисление пределов функций.

Теорема об арифметике позволяет не только устанавливать факт существования конечного предела, но и вычислять его.

Пример. .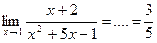

Однако, в ряде случаев теорема об арифметике не может быть применена.

Пример.

, .

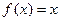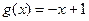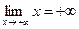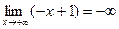, . Теорему применять нельзя, хотя

.

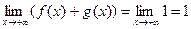В этих случаях говорят, что имеет место неопределенность. Для вычисления предела необходимо преобразовать функцию тождественным образом так, чтобы теорема об арифметике стала применима (т.е. раскрыть неопределенность).

К неопределенностям относят следующие ситуации:

, , , , , .

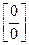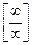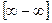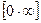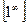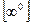Пример. .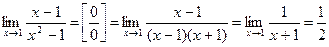

Замечательные пределы.

Теорема 1 (первый замечательный предел). Предел отношения синуса бесконечно малой дуги к самой дуге, выраженной в радианах, равен единице:

.

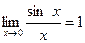Док-во. Рассмотрим круг радиуса R с центром в точке О. Пусть сначала 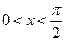. Из рисунка видно, что .

;

;

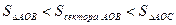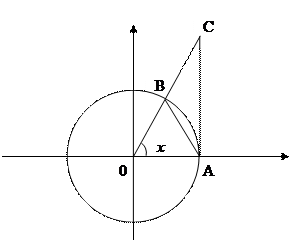
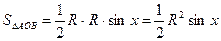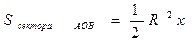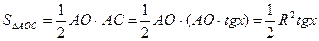.Таким образом,

.

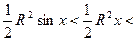
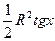Разделив обе части этого выражения на

>0, получим:

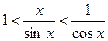или .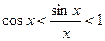

Переходя в этом неравенстве к пределу при 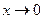, получим: .

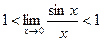По теореме о промежуточной функции .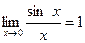

При 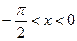полученные выводы также будут справедливы (доказать самостоятельно).▲

Следствия. ; ; .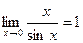

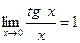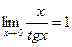Теорема 2 (второй замечательный предел). Числовая последовательность 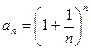имеет конечный предел, равный числу е:

, ()

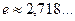Следствия. ; .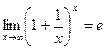

Примеры.

; .

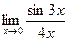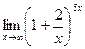К числу е приводят многие задачи из области физики, биологии, ядерной физики, демографии и т.п. Рассмотрим применение второго замечательного предела в экономических расчетах.

Задача о непрерывном начислении процентов.

1. Простые проценты. В банк под проценты положена денежная сумма 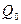. Ежегодная процентная ставка составляет р %. Каков будет размер вклада Q через t лет?

При использовании простых процентов размер вклада ежегодно увеличивается на одну и ту же величину.

Через год сумма составит ,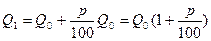

Через два года: ;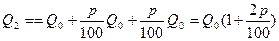

Через t лет:

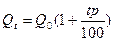- формула простых процентов.

2. Сложные проценты. При использовании сложных процентов начисляются «проценты на проценты», т.е. размер вклада увеличивается ежегодно в одно и то же число раз:

;

;

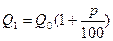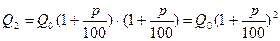- формула сложных процентов.

Как можно добиться максимального роста положенной на вклад суммы?

Один из возможных способов – воспользоваться услугами банка по начислению процентов не один раз в году, а более.

Если начислять проценты n раз в году, то процент начисления за 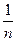часть года составит 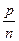%, а размер вклада за t лет при п ежегодных начислениях составит:

.

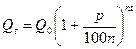Например, при р=100%:

;

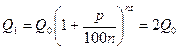Предположим, что через полгода счет закрыт с результатом

,

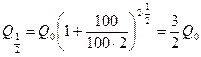а затем снова открыт в том же банке. Тогда через год сумма будет составлять

.

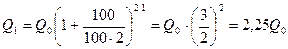При ежеквартальном повторении этих операций сумма в конце года составит:

;

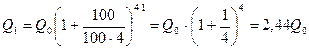При ежемесячном повторении этих операций:

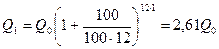и т.д.

Предположим (абстрактно), что проценты начисляются непрерывно, т.е. 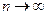. Тогда

.

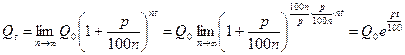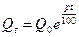- формула непрерывных процентов.

Таким образом, при 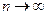в нашем примере 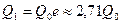, т.е. при непрерывном начислении процентов за год можно получить доход не более 172%, а через два года () можно увеличить начальный капитал более чем в 7 раз.

В практических финансово-кредитных операциях непрерывное начисление процентов не применяется, но используется в демографических, инвестиционных и др. расчетах.

Date: 2015-07-02; view: 831; Нарушение авторских прав