
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

свойство линейности смешанного произведения по каждому сомножителю
|
|
21)

22)

23)

24) 

25) 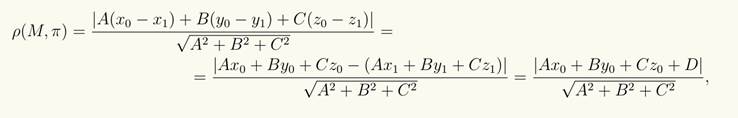
26) Определим прямую L на плоскости точками M0(x0; y0) на той же прямой и ненулевым вектором s = {l;m}, параллельным ей. Такой вектор s называется направляющим вектором прямой L.
Если точка M(x; y) принадлежит прямой, то это эквивалентно тому, что M0M
коллинеарен вектору s, т.е. эти векторы принадлежат одному и тому же пространству V1.
Так как вектор s не принадлежит нулевому, он образует базис в том же пространстве V1. Следовательно, для некоторого числа t выполняется равенство
M0M = ts. Воспользовавшись тем, что
M0M ={x − x0; y − y0; z-z0}, s = {m;l;p}, запишем равенство:
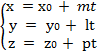
Такое уравнение называют параметрическим уравнением прямой.
Коллинеарность векторов M0M и s, эквивалентна равенству отношений их одноимённых координат:
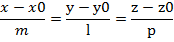
Такое уравнение называется каноническим.
27)Уравнение прямой, проходящей через две точки:
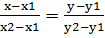 =
= 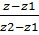
28) 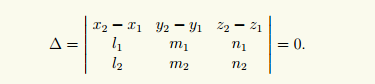
29) 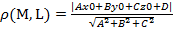
30)
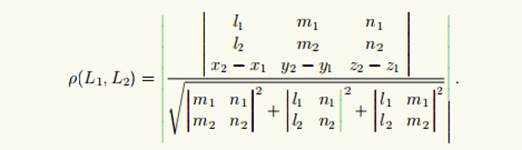
//////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
Теорема. (Критерий линейной зависимости системы векторов линейного пространства)
Для того, чтобы система векторов линейного пространства была линейно зависима, необходимо и достаточно, чтобы один из векторов являлся линейной комбинацией остальных векторов системы.
Доказательство: Необходимость. Пусть система векторов 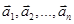 линейно зависима. Покажем, что один из векторов является линейной комбинацией остальных. Из определения линейной зависимости следует, что
линейно зависима. Покажем, что один из векторов является линейной комбинацией остальных. Из определения линейной зависимости следует, что 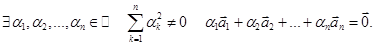 Предположим без ограничения общности, что
Предположим без ограничения общности, что 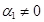 (в противном случае векторы могут быть перенумерованы). Разделим последнее равенство на
(в противном случае векторы могут быть перенумерованы). Разделим последнее равенство на 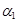 , получим:
, получим:
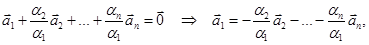
то есть вектор 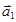 является линейной комбинацией остальных векторов.
является линейной комбинацией остальных векторов.
Достаточность. Пусть один из векторов является линейной комбинацией остальных, например, 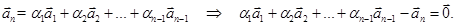
Таким образом, получена нетривиальная (коэффициент при 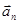 отличен от нуля) линейная комбинация векторов
отличен от нуля) линейная комбинация векторов 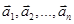 , равная нулю-вектору, следовательно, эти векторы линейно зависимы.
, равная нулю-вектору, следовательно, эти векторы линейно зависимы.
Теорема. (О разложении вектора по базису).
Всякий вектор может быть разложен по некоторому базису векторного пространства единственным образом. Доказательство: От противного. Рассмотрим разложение некоторого вектора 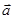 по произвольному базису
по произвольному базису 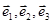 не единственно:
не единственно:
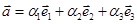 ;
;
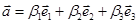 .
.
Вычитая равенства, получим 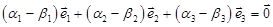 .Из определения 1.5.2 вытекает линейная независимость векторов
.Из определения 1.5.2 вытекает линейная независимость векторов 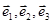 .
.
Следовательно, лишь тривиальная их линейная комбинация равна нулевому вектору, откуда 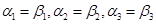 , что и требовалось доказать.
, что и требовалось доказать.
Теорема. (Свойство линейности скалярного произведения.)
1) Скалярное произведение дистрибутивно относительно сложениявекторов:
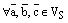 ,
, 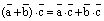 .
.
2) Скалярный множитель можно выносить за знак скалярного произведения:
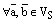 ,
, 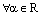 ,
, 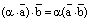 .
.
Доказательство. По свойству 4 предыдущей теоремы и по свойству проекции вектора на вектор (на ось) имеем:
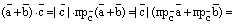
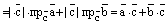 .
.
Теорема. (Выражение скалярного произведения двух векторов, заданных в ортонормированном базисе).
В ортонормированном базисе скалярное произведение двух векторов равно сумме попарных произведений их соответствующих координат. Доказательство:
Пусть в ортонормированном базисе 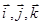 заданы векторы
заданы векторы
 ,
, 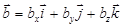 .
.
Заметим, что вследствие ортонормированности базиса
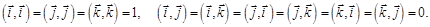
Тогда
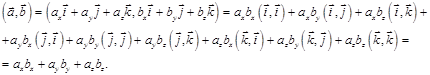
Теорема. (Выражение векторного произведения двух векторов, заданных в ортонормированном базисе). Координаты векторного произведения векторов 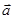 и
и 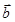 равны алгебраическим дополнениям элементов первой строки символического определителя
равны алгебраическим дополнениям элементов первой строки символического определителя
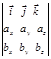 .
.
Доказательство: Пусть векторы 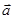 и
и 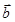 имеют в ортонормированном базисе разложения
имеют в ортонормированном базисе разложения
 ,
, 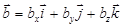 . Тогда по свойству 6 векторного произведения
. Тогда по свойству 6 векторного произведения
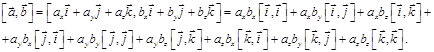
Используя предыдущую теорему 1.7.7, и очевидные равенства 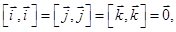 получим
получим
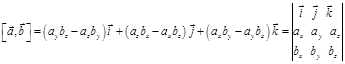 .
.
Теорема. (Свойства смешанного произведения).
3. 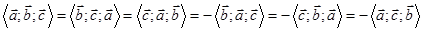 ;
;
4. 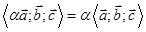 ;
;
5. 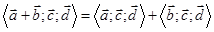 ;
;
4 следуют из определения смешанного произведения
3 следует из доказанной теоремы (Геометрический смысл смешанного произведения трех векторов).
5 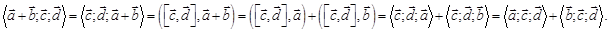
Теорема. (Выражение смешанного произведения двух векторов, заданных в ортонормированном базисе).
Смешанное произведение трех векторов в ортонормированном базисе равно определителю, строками которого являются координаты этих векторов данном базисе. Доказательство: Пусть векторы 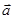 ,
, 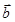 и
и 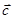 имеют в ортонормированном базисе разложения
имеют в ортонормированном базисе разложения
 ,
, 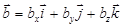 ,
, 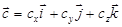 . Тогда
. Тогда
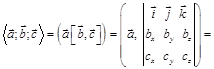
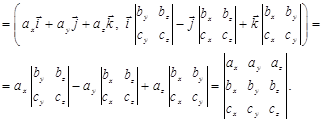



| <== предыдущая | | | следующая ==> |
| Опухоли яичников и беременность | | | Эталон ответа |
Date: 2015-07-02; view: 2375; Нарушение авторских прав