Теорема Бернулли и Чебышева

Теорема Бернулли утверждает: если т - количество событий А в п попарно независимых испытаниях, а р вероятность наступления события А в каждом из испытаний, то при любом является 0 справедлива неравенство

Эта формула является первым в истории вариантом закона больших чисел и по сути считается началом теории вероятностей как области математической науки того времени теории выборочного метода становятся основой математически й статистики.

Теорема Бернулли дает возможность оценить количество независимых испытаний п при определенных условиях их проведения

Теорема Чебышева гласит: если случайные величины Х, Х₂, X_n попарно независимы и существует число C такое, что D [Xi C для всех / '= 1, 2, n, то для любого является 0 справедлива неравенство

Г x иx 2 Xn _ м[x им[x 2м[Xn 1 с_ ₍₃₄₁₎

[n n J ne¹

Неравенство (341) можно представить иначе

lim p - ± X, - ± M [X есть = 1 (342)

Следовательно, вероятность того, что среднее арифметическое независимых случайных ₁ n

величин - X X_i отличается от среднего арифметического математических ₁ n

надежд - X M [X_i менее на есть, приближается к 1 при росте числа

n

случайных величин, для любого является

Теорема Чебышева является развитием и обобщением теоремы Бернулли Для практических целей чаще всего используется такой вариант испытаний, когда все X имеют одинаковые показатели математического ожидания М мхи = М и дисперсии DPA ^ D Тогда в качестве оценки математического ожидания используется выборочное среднее арифметическоее

Рассмотрим последовательность случайных величин 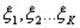(2).

Введем среднее арифметическое:

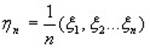
Запишем математическое ожидание:

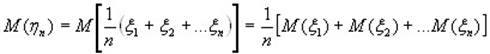
Обозначим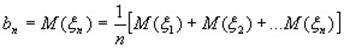

Def: говорят, что для последовательности (2) выполняется закон больших чисел, если для любого 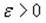справедливо равенство:

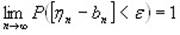
(3).

О равенстве (3) также говорят, что среднее арифметическое случайных величин в вероятностном смысле (по вероятности) сходится к среднему арифметическому их математических ожиданий.

Если последовательность случайных величин (2) удовлетворяет закону больших чисел, то, как видно из равенства (3), среднее арифметическое 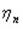ведет себя фактически как величина неслучайная, поскольку ее значение в вероятностном смысле как угодно мало отличается от числа 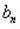(среднего арифметического математического ожидания случайной величины ).

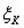Теорема Чебышева: пусть случайные величины 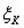последовательности (2) таковы, что:

1) Они попарно независимы.

2) Имеют конечное математическое ожидание.

3) Имеют равномерно ограниченные дисперсии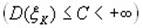

Тогда к последовательности применим закон больших чисел.

Доказательство.

Оценим дисперсию:

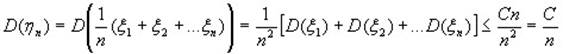
Применим неравенство (1):

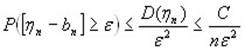
Левую часть выразим через вероятность противоположного события:

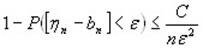
Умножим обе части на (-1):

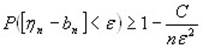
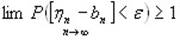
С другой стороны:

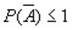
На основании двух предыдущих формул получаем формулу (3)

Теорема Бернулли: относительная частота события “А” в вероятностном смысле сходится к вероятности этого события:

(4)

Доказательство.

С каждым испытанием свяжем случайную величину .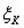

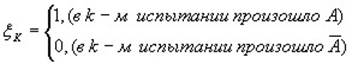
Тогда число наступлений события “А” в “n” независимых испытаний будет равно:

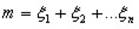
Покажем, что к этой последовательности применим закон больших чисел (равенство 3). Проверим выполнение условий теоремы Чебышева:

1) 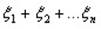– попарно независимы.

2)

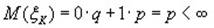
3)

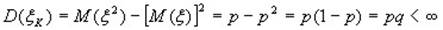
Таким образом в силу теоремы Чебышева к последовательности случайных величин { 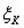} применим закон больших чисел, выражаемый равенством (3). В данном случае среднее арифметическое: 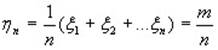– относительная частота.

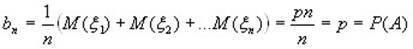
В силу (3) получаем равенство (4).

Теорема доказана.

Date: 2015-07-02; view: 579; Нарушение авторских прав