
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Ответ. Площадь фигуры равна 125/6
|
|
ЛАБОРАТОРНАЯ РАБОТА №2
ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
ПРИМЕР ВЫПОЛНЕНИЯ ЛАБОРАТОРНОЙ РАБОТЫ №2
Задача 1. Найти площадь фигуры, ограниченной линиями: 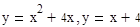 .
.
1. Построим графики функций.
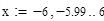
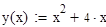
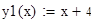
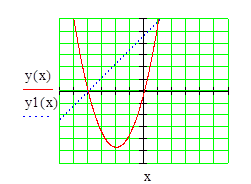
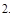 Найдем абсциссы точек пересечения.
Найдем абсциссы точек пересечения. 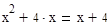
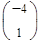
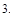 Вычислим площадь фигуры. Воспользуемся формулой:
Вычислим площадь фигуры. Воспользуемся формулой: 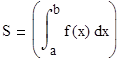
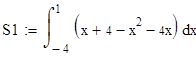
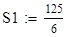
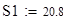 .
.
Ответ. Площадь фигуры равна 125/6
Задача 2. Найти экстремумы, точки перегиба и наибольшее и наименьшее значение функции
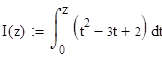 на отрезке [3/2; 4]. Построить графики функции и производных.
на отрезке [3/2; 4]. Построить графики функции и производных.
Решение. По теореме о производной определенного интеграла с переменным верхним пределом 1-ая производная равна подынтегральной функции от верхнего предела: 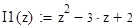 .
.
Найдем критические точки: 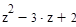 .
. 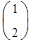
Найдем 2-ую производную функции I(z)
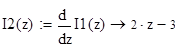
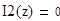 при
при 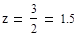
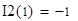
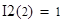
По значениям 2-ой производной в точках z=1 и z=2 делаем вывод, что
1) точка z=1 – точка максимума и максимальное значение 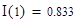 ;
;
2) z=2 – точка минимума, минимальное значение функции 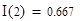 ;
;
3) z=3/2 – абсцисса точки перегиба, ордината, т.е. 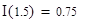 .
.
Наибольшее и наименьшее значения функции на отрезке [3|2;4] находим, сравнивая значения функции на концах отрезка и в критических точках внутри отрезка:
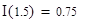 ,
, 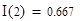 ,
, 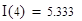 .
.
ОТВЕТ. Точка z=1 - точка максимума, максимальное значение - 0.833; z=2 - точка минимума, минимальное значение - 0.667, М(1.5; 0.75) - точка перегиба. На отрезке [3/2; 4] наибольшее значение функции - 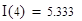 , а наименьшее -
, а наименьшее - 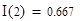 .
.
Для проверки (подтверждения выводов) строим графики функции и ее производных (1 и 2).
Задача 3. Найти площадь, ограниченную линиями, заданными в полярной системе координат:
r = 2sinf, r = 4sinf.
Будем использовать формулу: 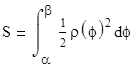
1. Построим графики кривых в полярной системе координат.
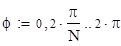
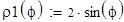
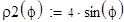
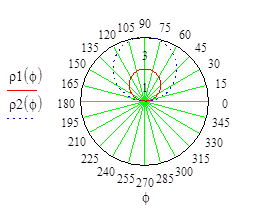
2. Вычислим площадь полвины всей фигуры, воспользовавшись симметрией относительно луча f = 90 (см. графики).
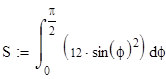
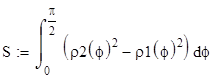
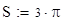 .
.
| <== предыдущая | | | следующая ==> |
| | | Кафедра онкологии, гематологии и лучевой терапии |
Date: 2015-07-02; view: 308; Нарушение авторских прав