
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Исследование систем линейных алгебраических уравнений в пакете MathCAD
|
|
Пример №1.
Задание. Показать, что столбцы 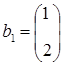 и
и 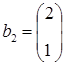 , составленные из коэффициентов уравнений
, составленные из коэффициентов уравнений
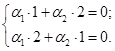
являются линейно независимыми.
______________________________________________________
Последовательность действий.
1. Ввести сопроводительный текст "Пример №1" в правом верхнем углу листа.
Установить шрифт - MS Sans Serif сопроводительного текста, поддерживающий кириллицу. Для этого надо модифицировать текстовый стиль "Normal":
§ Выбрать пункт меню Format4Style (Формат4Стиль) и загрузить диалоговое окно Text Styles (Стили текста)
(Рис. 3.1).
§ В диалоговом окне Text Styles (Стили текста) выбрать из списка Styles (Стили) стиль "Normal", нажать кнопку Modify (Изменить) и загрузить диалоговое окно Define Style (Стиль по умолчанию) (Рис. 3.2).
§ В диалоговом окне Define Style (Стиль по умолчанию) нажать кнопку Font (Шрифт) и загрузить диалоговое окно Text Format (Формат текста) (Рис. 3.3).
§ В списке Font (Шрифт) выбрать тип шрифта – MS Sans Serif и последовательно нажав кнопку OK (Да) закрыть диалоговые окна Text Format (Формат текста) и Style (Стиль по умолчанию).
§ Закрыть диалоговое окно Text Styles (Стили текста), нажав кнопку Close (Закрыть).
Перейти в русскую раскладку клавиатуры.
q Установить курсор (красный крест) в верхнем правом углу листа, щелкнув правой кнопкой мыши.
q Перейти в текстовый регион (при русской раскладке клавиатуры нажать кнопки "Shift" + "2"),  .
.
q Ввести текст "Пример № 1",  .
.
Завершить процесс ввода сопроводительного текста, щелкнув левой кнопкой мыши на свободном месте листа,
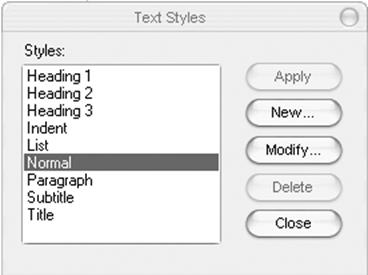
Рис. 3.1. Диалоговое окно Text Styles (Стили текста)
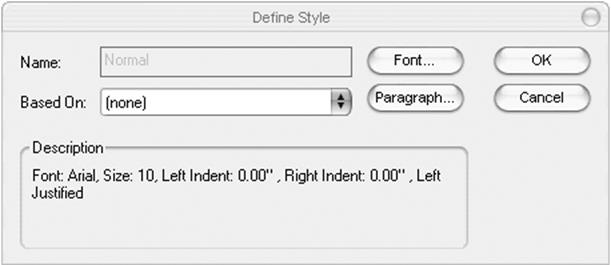
Рис. 3.2. Диалоговое окно Define Style (Стиль по умолчанию)
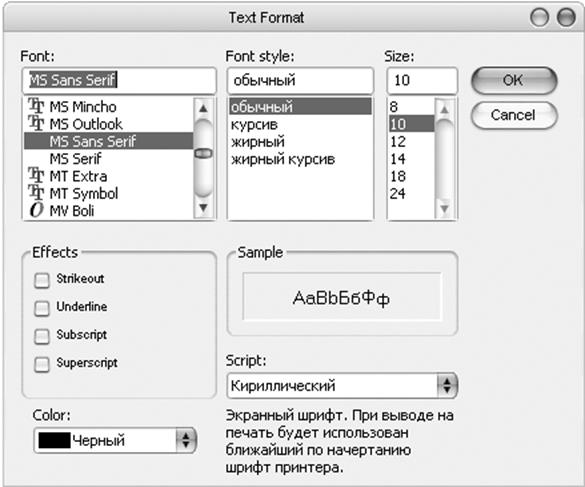
Рис. 3.3. Диалоговое окно Text Format (Формат текста)
2. Решить систему уравнений методом Крамера:
Ввести сопроводительный текст "Матрицы коэффициентов" (см. Рис. 3.4).
Составить матрицы коэффициентов –:
Матрица - D (см. Рис. 3.4):
§ Выбрать место для ввода матрицы коэффициентов.
§ Ввести имя матрицы, D, из панели инструментов  математической панели.
математической панели.
§ Ввести знак присвоения, нажав клавиши "Shift" + ":", 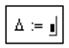
§ Ввести шаблон матрицы 2х2, нажав клавиши "Ctrl"+"M" и заполнив текстовые строки Rows (Строки) и Columns (Столбцы) цифрами -2 в диалоговом окне Insert Matrix (Вставить матрицы).
§ Заполнить ячейки шаблона, 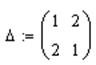
Матрица - D1 (Рис. 3.4):
§ Выбрать место для ввода матрицы коэффициентов (см.)
§ Ввести символ, D, из панели инструментов 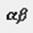 математической панели.
математической панели.
§ Перейти в режим ввода нижнего индекса в имени переменной, нажав клавишу точка ".".
§ Вести 1
§ Ввести знак присвоения, шаблон матрицы 2х2 и заполнить ее последний, как это было сделано выше, 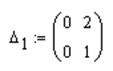 .
.
§ Матрица - 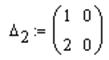 (проделать самостоятельно) (см. Рис. 3.4).
(проделать самостоятельно) (см. Рис. 3.4).
Ввести сопроводительный текст "Решить систему уравнений и найти неизвестные переменные" (см. параграф "Ввод пояснительного текста").
Найти значение переменной a1.
Рассчитать определитель матрицы D (см. Рис. 3.4).
§ Выбрать место на экране и ввести имя переменной и знак присвоения, detD:=.
§ Ввести имя матрицы D и символ определителя матрицы |D|, нажав клавиши "Shift" +"|", detD:=|D|
§ Просмотреть содержимое переменной. Ввести имя переменной и знак просмотра, нажав кнопку "=", detD=-3.
Рассчитать определитель матрицы D1, detD1:=|D1|, detD1=0 (проделать самостоятельно) (см. Рис. 3.4).
Рассчитать значение коэффициента a1 (см. Рис. 3.4).
§ Ввести имя переменной, a1 и знак присвоения, 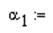
§ Ввести переменную detD1.
§ Ввести знак деления, нажав клавишу "/",  .
.
§ Ввести в качестве делителя (в черный прямоугольник) переменную detD, 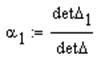
§ Просмотреть содержимое переменной. Ввести имя переменной и знак просмотра, нажав кнопку "=", a1=0.
Найти значение переменной a2.
Рассчитать определитель матрицы D2, detD2:=|D2|, detD2=0 (проделать самостоятельно) (см. Рис. 3.4).
q Рассчитать и просмотреть значение коэффициента a2,  (проделать самостоятельно) (см. Рис. 3.4).
(проделать самостоятельно) (см. Рис. 3.4).
q Просмотреть значение коэффициента a2,  (проделать самостоятельно) (см. Рис. 3.4).
(проделать самостоятельно) (см. Рис. 3.4).
Следовательно, система уравнений имеет решение только в том случае, когда переменные a1 и a2 равны 0. Следовательно, столбцы b1 и b2 линейно не зависимы.
На (см. Рис. 3.4) приведен листинг с примером №1.
Пример №2
Задание. Показать, что столбцы
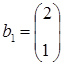 ,
, 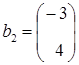 ,
, 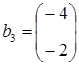
линейно зависимы, используя операцию умножения векторов на скаляр.
___________________________________________________
Последовательность действий.
1. Ввести сопроводительный текст "Пример № 2" в правом верхнем углу листа. (см. Пример №1 п.1)
2. Определить векторы-столбцы 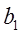 ,
, 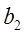 ,
, 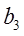 .
.
q Ввести сопроводительный текст "Исходные векторы" (см. Пример №1 п.1)

Рис. 3.4. Листинг программы MathCAD (Пример №1)
q Определить векторы 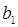 (последовательность действий см. в Примере №1 п.2),
(последовательность действий см. в Примере №1 п.2),  ,
,
q Определить вектор 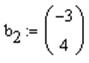 , скопировав и отредактировав вектор
, скопировав и отредактировав вектор 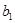 . Общий подход описан в параграфе "Редактирование и манипулирование формулами"
. Общий подход описан в параграфе "Редактирование и манипулирование формулами"
§ Щелкнуть указателем мыши на выражении 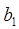 .
.
q Манипулируя клавишами "стрелки" и "пробел" переместить и охватить выражение синим уголком. 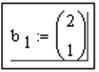
§ Скопировать выражение в буфер обмена, нажав кнопки "Ctrl"+"Insert"
§ Вставить скопированное выражение, для этого:
§ Расположить указатель мыши правее выражения 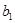 и нажать левую кнопку мыши. На месте вставки выражения появиться красный крестик
и нажать левую кнопку мыши. На месте вставки выражения появиться красный крестик  ,
,
§ Вставить выражение из буфера обмена, нажав клавиши "Shift"+"Insert", 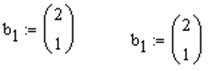 .
.
§ Отредактировать выражение (подробности см. в параграфе "Редактирование формул").
§ Щелкнуть на формуле и манипулируя стрелками разместить курсор перед цифрой "1", 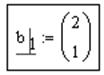 ,
,
§ Удалить цифру "1", нажав клавишу "Delete".
§ Ввести цифру "2".
§ Остальные элементы выражения отредактировать самостоятельно (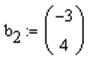 ).
).
q Определить вектор 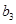 , скопировав и отредактировав вектор
, скопировав и отредактировав вектор 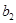 . Проделать самостоятельно. В результате исходные векторы столбцы
. Проделать самостоятельно. В результате исходные векторы столбцы 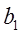 ,
, 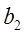 ,
, 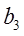 на экране примут вид
на экране примут вид
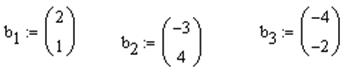
q Произвести горизонтальное выравнивание выражений.
Проделать самостоятельно. Подробности см. в параграфе "Горизонтальное выравнивание объектов (текста и формул)". В результате выражения примут вид.
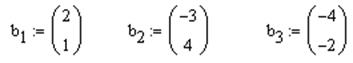
2. Подобрать скалярные коэффициенты 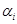 таким образом, что выполняется условие
таким образом, что выполняется условие
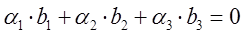 , где 0 –вектор, элементы которого равны 0. Если не все коэффициенты
, где 0 –вектор, элементы которого равны 0. Если не все коэффициенты 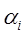 =0, то векторы-столбцы линейно зависимы.
=0, то векторы-столбцы линейно зависимы.
Ввести сопроводительный текст "Подбор числовых коэффициентов" по середине листа. (см. Пример №1 п.1)
Определить векторы-столбцы 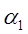 ,
, 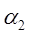 ,
, 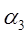 .
.
Проделать самостоятельно (см. п.1 настоящего примера). В результате выражение примет вид 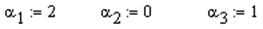 .
.
3. Проверить правильность подбора коэффициентов.
Ввести сопроводительный текст "Проверка" по середине листа. (см. Пример №1 п.1)
Произвести умножение вектора на скалярный коэффициент (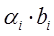 , где i- меняется от 1 до 3) и суммирование полученных результатов
, где i- меняется от 1 до 3) и суммирование полученных результатов 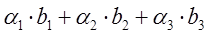
Последовательность операций.
§ Установить точку ввода выражения, расположив курсор ниже и левее слова "Проверка" и щелкнув левой кнопкой мыши. В точке ввода появится красный крестик.
§ Ввести имя переменной "sum"
§ Ввести знак присвоения, нажав клавиши "Shift" + ":",
(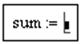 )
)
§ Ввести переменную 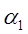
§ Ввести знак умножения, нажав клавиши "Shift" + "*"
§ Ввести переменную 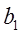 ,
,
§ Ввести знак сложения, нажав кнопки "Shift" + "+"
В результате получим выражение (Рис. 3.5 а))
§ Самостоятельно пописать два оставшихся слагаемых.
В результате получим выражение (Рис. 3.5 б))
Просмотреть результаты расчета.
§ Ввести правее выражения имя переменной "sum"
§ Ввести знак равенства, нажав клавишу "="
В результате получим выражение (Рис. 3.5 в)).
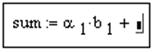 а)
а)
|
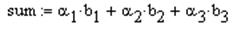 б)
б)
|
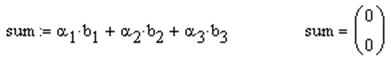 в)
в)
|
Рис. 3.5. Арифметические операции с вектором (Пример№2)
Следует отметить, что имя переменной "sum" должно располагаться на одном уровне или немного ниже выражения, так как расчеты ведутся всегда слева на право и сверху в низ. В противном случае переменная "sum" окрасится в красный цвет и выражение примет вид 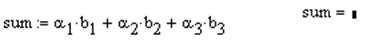
На Рис. 3.6 приведен листинг примера №2.
Пример №3
Задание. Выписать все миноры матрицы
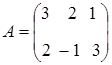 .
.
___________________________________________________
Последовательность действий.
1. Ввести сопроводительный текст "Пример № 3" в правом верхнем углу листа. (см. Пример №1 п.1)
2. Определить матрицу А
q Ввести сопроводительный текст "Исходная матрица" (см. Пример №1 п.1)
q Определить и заполнить матрицу А, используя шаблон матрицы (последовательность действий см. в Примере №1 п.2)
3.Определить миноры матрицы А
Ввести сопроводительный текст "Миноры матрица А"
(см. Рис. 3.7)

Рис. 3.6. Листинг программы MathCAD (Пример №2)
q Определить первый минор М1, полученный вычеркиванием 2-х строк и 1-го и 2-го столбцов матрицы А, используя функцию submatrix(A,ir,jr,ic,jc) (см. параграф "Функция submatrix(A,ir,jr,ic,jc)"). Последовательность действий и расположение выражения на экране монитора приведена на
Рис. 3.7. Следует учесть, что индекс первой строки и первого столбца матрицы равен 0. Следовательно, аргументы в функции примут вид submatrix(A,0,1,0,1)
q Определить второй минор М2, полученный вычеркиванием 2-х строк и 1-го и 3-го столбцов матрицы А, используя функцию чтения столбца матрицы (см. параграф "Верхний индекс и столбцы матрицы") и функцию augment(A,B) (см. параграф "Функции augment(A,B) и stack(A,B)"). Последовательность действий и расположение выражения на экране монитора приведена на
Рис. 3.7.
q Определить третий минор М31, полученный вычеркиванием 2-х строк и 2-го и 3-го столбцов матрицы А, используя функцию submatrix(A,ir,jr,ic,jc).
q Определить третий минор М32, полученный вычеркиванием 2-х строк и 2-го и 3-го столбцов матрицы А, используя функцию чтения столбца матрицы и функцию. Последовательность действий и расположение выражения на экране монитора приведена на Рис. 3.7.
4. После завершения расчетов выровнять выражения по вертикали и горизонтали, как показано на Рис. 3.7. Последовательность действий см. в параграфе "Выравнивание формул и сопроводительного текста"
На Рис. 3.7 приведен листинг примера №3.

Рис. 3.7. Листинг программы MathCAD (Пример №3)
Пример №4
Задание. Определить ранг матрицы
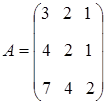 .
.
___________________________________________________
Последовательность действий.
1. Ввести сопроводительный текст "Пример № 4" в правом верхнем углу листа. (см. Пример №1 п.1)
2. Определить матрицу А
q Ввести сопроводительный текст "Исходная матрица" (см. Пример №1 п.1)
q Определить и заполнить матрицу А, используя шаблон матрицы (последовательность действий см. в Примере №1 п.2)
3. Определить ранг матрицы А, используя функцию rank(A). (подробности см. в параграфе "Функции определения следа и ранга матрицы"). Последовательность действий и расположение выражения на экране монитора приведена на Рис. 3.8.
Для определения ранга матрицы необходимо: выбрать место для ввода выражения и нажать левую кнопку мыши (появится красный крестик), ввести имя переменной (rankA), ввести знак присвоения (кнопки "Shift"+":"), ввести имя функции (rank()), ввести аргумент функции (переменную А).
4. После завершения расчетов выровнять выражения по горизонтали, как показано на Рис. 3.8. Последовательность действий см. в параграфе "Выравнивание формул и сопроводительного текста"
На Рис. 3.8Рис. 3.7 приведен листинг примера №4.
Пример №5
Задание. Определить все базисные миноры матрицы
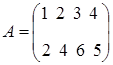
___________________________________________________
Последовательность действий.
1. Ввести сопроводительный текст "Пример № 5" в правом верхнем углу листа. (см. Пример №1 п.1)
2. Определить матрицу А
Ввести сопроводительный текст "Исходная матрица" (см. Пример №1 п.1)

Рис. 3.8. Листинг программы MathCAD (Пример №4)
Определить и заполнить матрицу А, используя шаблон матрицы (последовательность действий см. в Примере №1 п.2)
3. Определить все миноры матрицы А.
q Ввести сопроводительный текст "Миноры матрица А"
q Определить миноры матрицы, используя функцию submatrix(A,ir,jr,ic,jc) (см. параграф "Функция submatrix(A,ir,jr,ic,jc)").
Для выполнения операции надо ввести имя переменной, знак присвоения (нажав клавиши "Shift" + ":"), ввести функцию submatrix(A,ir,jr,ic,jc) с соответствующими параметрами Последовательность действий и расположение выражения на экране монитора приведена на Рис. 3.9. Следует учесть, что индекс первой строки и первого столбца матрицы равен 0.
5. Просмотреть содержание переменных.
Для выполнения операции надо разместить курсор правее места ввода выражения для определения минора, нажать левую. кнопку мыши, ввести имя переменной содержащий минор и ввести знак равенства (нажав клавишу "="). Последовательность действий и расположение выражения на экране монитора приведена на
Рис. 3.9.
6. Рассчитать определители миноров.
q Ввести сопроводительный текст "Определители миноров"
q Рассчитать определители миноров.
Для выполнения операции надо ввести имя переменной, содержащей минор, ввести функцию определителя (нажав клавиши "Shift" + "|") и знак равенства (нажав клавишу "="). Подробнее о функции определителя матрицы см. в параграфе "Элементарные матричные вычисления"). Последовательность действий и расположение выражения на экране монитора приведена на Рис. 3.9.
7. Выписать базисные миноры.
Последовательность действий и расположение выражения на экране монитора приведена на Рис. 3.9.
8. После завершения расчетов выровнять выражения по горизонтали, как показано на Рис. 3.9.
На Рис. 3.9 приведен листинг примера №5.

Рис. 3.9. Листинг программы MathCAD (Пример №5)
Пример №6
Задание. Исследовать совместность системы линейных алгебраических уравнений
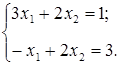
___________________________________________________
Последовательность действий.
1. Ввести сопроводительный текст "Пример № 6" в правом верхнем углу листа. (см. Пример №1 п.1)
2. Определить:
- матрицу А, состоящую из коэффициентов левой части СЛАУ,
- вектор В, состоящий из коэффициентов правой части СЛАУ
- расширенную матрицу С, состоящую из коэффициентов левой и правой частей СЛАУ.
q Ввести сопроводительный текст "Исходные данные" (см. Пример №1 п.1)
q Определить и заполнить матрицу А, В, используя шаблон матрицы (последовательность действий см. в Примере №1 п.2).
Для определения матрицы А необходимо: выбрать место для размещения матрицы, щелкнуть левой кнопкой мыши (появится красный крест), ввести имя переменной (А), ввести знак присвоения (клавиши "Shift"+":"), вызвать диалоговое окно Insert Matrix (Вставить матрицу) (клавиши "Ctrl"+"M"), ввести в текстовые окна Rows (Строки), Columns (Колонки) цифру 2, закрыть диалоговое окно, заполнить ячейки шаблона матрицы коэффициентами левой части системы уравнений.
По аналогии определить матрицы В.
Последовательность действий и расположение выражения на экране монитора приведена на Рис. 3.10.
q Определить расширенную матрицу С, используя функцию augment(A,B) (см. параграф "Функции augment(A,B) и stack(A,B)") (последовательность действий см. в Примере №3) и вывести на экран значение полученной матрицы.
Расположение выражения на экране монитора приведена на Рис. 3.10.
3. Определить ранг матриц А и С (см. Пример №4).
q Ранги матриц A и С равны (rankA=rankC), следовательно система уравнений совместна и имеет решение.
Последовательность действий и расположение выражения на экране монитора приведена на Рис. 3.10.
4. Решить систему уравнений методом Крамера.
q Ввести сопроводительный текст в две строки "Решить систему уравнений методом Крамера" и "Дополнительные матрицы".
q Определить дополнительные матрицы А1 и А2. Матрица А1 получается заменой первого столбца матрицы А вектором В, а матрица А2 - заменой второго столбца матрицы А вектором В.
Для получения матриц А1 и А2 использовать функцию чтения столбца матрицы (см. параграф "Верхний индекс и столбцы матрицы") и функцию augment(A,B) (см. параграф "Функции augment(A,B) и stack(A,B)") (см. Пример№3).
Последовательность действий и расположение выражения на экране монитора приведена на Рис. 3.10.
q Ввести сопроводительный текст "Расчет неизвестных".
q Рассчитать две неизвестных х1 и х2.
Для расчета неизвестной переменной х1 необходимо найти частное от деления определителя матрицы А1 на определитель матрицы А.
В MatchCAD для этого необходимо: выбрать место для размещения выражения и нажать левую кнопку мыши (появится красный крестик), ввести мя переменной - х1 (нажать клавиши "х", ".", "1"), ввести знак присвоения (клавиши "Shift"+":"), ввести имя матрицы А1, ввести функцию определителя (кнопки "Shift"+"|"), ввести знак деления (кнопка "/"), ввести имя матрицы А, ввести функцию определителя (кнопки "Shift"+"|").
q Аналогично определить неизвестную переменную х2. Вывести полученные значения переменных.
Последовательность действий и расположение выражения на экране монитора приведена на Рис. 3.10.
На Рис. 3.10 приведен листинг примера №6.
Пример №7
Задание. Исследовать совместность системы линейных алгебраических уравнений
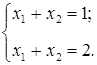

Рис. 3.10. Листинг программы MathCAD (Пример №6)
___________________________________________________________
Последовательность действий.
1. Ввести сопроводительный текст "Пример № 7" в правом верхнем углу листа. (см. Пример №1 п.1)
2. Определить:
- матрицу А, состоящую из коэффициентов левой части СЛАУ,
- вектор В, состоящий из коэффициентов правой части СЛАУ
- расширенную матрицу С, состоящую из коэффициентов левой и правой частей СЛАУ.
q Ввести сопроводительный текст "Исходные данные" (см. Пример №1 п.1)
q Определить и заполнить матрицу А, В, используя шаблон матрицы (последовательность действий см. в Примере №1 п.2).
Для определения матрицы А необходимо: выбрать место для размещения матрицы, щелкнуть левой кнопкой мыши (появится красный крест), ввести имя переменной (А), ввести знак присвоения (клавиши "Shift"+":"), вызвать диалоговое окно Insert Matrix (клавиши "Ctrl"+"M"), ввести в текстовые окна Rows, Columns цифру 2, закрыть диалоговое окно, заполнить ячейки шаблона матрицы коэффициентами левой части системы уравнений.
q По аналогии определить матрицы В.
Последовательность действий и расположение выражения на экране монитора приведена на Рис. 3.11.
q Определить расширенную матрицу С, используя функцию augment(A,B) (см. параграф "Функции augment(A,B) и stack(A,B)") (последовательность действий см. в Примере №3) и вывести на экран значение полученной матрицы.
Расположение выражения на экране монитора приведена на
Рис. 3.11.
3. Определить ранг матриц А и С (см. Пример №4).
Ранги матриц A и С равны (rankA<rankC), следовательно система уравнений не совместна и не имеет единственного решения.
Последовательность действий и расположение выражения на экране монитора приведена на Рис. 3.11.
На Рис. 3.11 приведен листинг примера №7.
Пример №8
Задание. Исследовать совместность системы линейных алгебраических уравнений
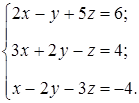
___________________________________________________
Последовательность действий.
1. Ввести сопроводительный текст "Пример № 8" в правом верхнем углу листа. (см. Пример №1 п.1)
2. Определить:
- матрицу А, состоящую из коэффициентов левой части СЛАУ,
- вектор В, состоящий из коэффициентов правой части СЛАУ
- расширенную матрицу С, состоящую из коэффициентов левой и правой частей СЛАУ.
q Ввести сопроводительный текст "Исходные данные" (см. Пример №1 п.1)

Рис. 3.11. Листинг программы MathCAD (Пример №7)
q Определить и заполнить матрицу А, В, используя шаблон матрицы (последовательность действий см. в Примере №1 п.2).
Для определения матрицы А необходимо: выбрать место для размещения матрицы, щелкнуть левой кнопкой мыши (появится красный крест), ввести имя переменной (А), ввести знак присвоения (клавиши "Shift"+":"), вызвать диалоговое окно Insert Matrix (клавиши "Ctrl"+"M"), ввести в текстовые окна Rows, Columns цифру 3, закрыть диалоговое окно, заполнить ячейки шаблона матрицы коэффициентами левой части системы уравнений.
q По аналогии определить матрицы В (ввести в текстовые окна Rows цифру 3, Columns цифру 1).
Последовательность действий и расположение выражения на экране монитора приведена на Рис. 3.12.
q Определить расширенную матрицу С, используя функцию augment(A,B) (см. параграф "Функции augment(A,B) и stack(A,B)") (последовательность действий см. в Примере №3) и вывести на экран значение полученной матрицы.
Расположение выражения на экране монитора приведена на
Рис. 3.12.
3. Определить ранг матриц А и С (см. Пример №4).
Ранги матриц A и С равны (rankA=rankC), следовательно система уравнений совместна и имеет единственное решение.
Последовательность действий и расположение выражения на экране монитора приведена на Рис. 3.12.
4. Решить систему уравнений методом Крамера.
q Ввести сопроводительный текст в две строки "Решить систему уравнений методом Крамера" и "Дополнительные матрицы".
q Определить дополнительные матрицы А1 и А2. Матрица А1 получается заменой первого столбца матрицы А вектором В, матрица А2 - заменой второго столбца матрицы А вектором В, а матрица А3 - заменой третьего столбца матрицы А вектором В.
q Для получения матриц А1 и А2, А3 использовать способ замены i-столбца матрицы Аi вектором В.
Последовательность действий рассмотрим на примере матрицы А1:
§ Скопировать в матрицу А1 матрицу А.
Для этого необходимо выбрать место на экране монитора и нажать левую кнопку мыши (появится красный крестик обозначающий место ввода выражения), ввести переменную А1 (последовательно нажать клавиши "Shift" +"A", ".", "1"), ввести знак присвоения (клавиши "Shift" +":"), ввести переменную А (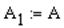 ).
).
§ Заменить первый столбец матрицы А1 вектором В.
Для этого необходимо выбрать место на экране монитора и нажать левую кнопку мыши (появится красный крестик обозначающий место ввода выражения), ввести переменную А1 (последовательно нажать клавиши "Shift" +"A", ".", "1"),ввести верхний индекс (клавиши "Ctrl"+"6", см. параграф "Верхний индекс и столбы матрицы"), ввести в угловые скобки индекс столбца, который надо заменить (ввести число 0), ввести знак присвоения (клавиши "Shift" +":"), ввести переменную В (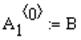 ).
).
§ Просмотреть значения матрицы А1.
Ввести переменную А1, ввести знак равенства (клавише "=")
Последовательность действий и расположение выражений на экране монитора для матриц А1 и А2, А3 приведена на Рис. 3.12.
5. Рассчитать три неизвестных х1 и х2, х3.
q Ввести сопроводительный текст "Расчет неизвестных".
q Для расчета неизвестной переменной х1 необходимо найти частное от деления определителя матрицы А1 на определитель матрицы А.
В MatchCAD для этого необходимо: выбрать место для размещения выражения и нажать левую кнопку мыши (появится красный крестик), ввести мя переменной - х1 (нажать клавиши "х", ".", "1"), ввести знак присвоения (клавиши "Shift"+":"), ввести имя матрицы А1, ввести функцию определителя (кнопки "Shift"+"|"), ввести знак деления (кнопка "/"), ввести имя матрицы А, ввести функцию определителя (кнопки "Shift"+"|").
q Аналогично определить неизвестную переменную х2, х3.
q Вывести полученные значения переменных.
Последовательность действий и расположение выражений х1 и х2, х3 на экране монитора приведена на Рис. 3.12.
На Рис. 3.12 приведен листинг примера №8.
1.3 Пример №9
Задание. Исследовать совместность системы линейных алгебраических уравнений
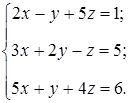
___________________________________________________
Последовательность действий.
1. Ввести сопроводительный текст "Пример № 9" в правом верхнем углу листа. (см. Пример №1 п.1)
2. Определить матрицу А, состоящую из коэффициентов левой части СЛАУ,

Рис. 3.12. Листинг программы MathCAD (Пример №8)
q Ввести сопроводительный текст "Исходные данные"
(см. Пример №1 п.1)
q Определить и заполнить матрицу А используя шаблон матрицы (последовательность действий см. в Примере №1 п.2).
Для определения матрицы А необходимо: выбрать место для размещения матрицы, щелкнуть левой кнопкой мыши (появится красный крест), ввести имя переменной (А), ввести знак присвоения (клавиши "Shift"+":"), вызвать диалоговое окно Insert Matrix (клавиши "Ctrl"+"M"), ввести в текстовые окна Rows, Columns цифру 3, закрыть диалоговое окно, заполнить ячейки шаблона матрицы коэффициентами левой части системы уравнений.
Последовательность действий и расположение выражения на экране монитора приведена на Рис. 3.13.
3. Определить ранг матриц А (см. Пример №4).
q Определить ранг матриц А
Для определения ранга матрицы А необходимо: выбрать место для размещения матрицы, щелкнуть левой кнопкой мыши (появится красный крест), ввести имя переменной (rankA) (нажать клавиши "rank" +"Shift"+"A"), ввести знак присвоения (клавиши "Shift"+":"), ввести имя функции (rank()), ввести аргумент функции (поместить курсор в круглых скобках и нажать клавиши "Shift"+"A")
q Просмотреть содержимое переменной rankA. (rankA=2). Ранг матрицы равен 2.
Для просмотра содержимого переменной rankA необходимо: ввести переменную rankA (нажать клавиши " rank" +"Shift"+"A"), ввести знак равенства (клавиша "=").
Таким образом, ранг матрицы А равен 2 (rankA=2), так как третья строка является суммой элементов первой и второй строки, то же можно сказать и об элементах расширенной матрицы. Последнее означает, что из системы уравнений последнее уравнение можно исключить
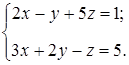
3. Определить:
- матрицу, состоящую из коэффициентов левой части новой СЛАУ,
- вектор, состоящий из коэффициентов правой части новой СЛАУ
Приведем новую СЛАУ к виду
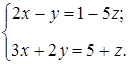
переменная z может принимать любые значения.
q Ввести сопроводительный текст "Исходные данные для новой СЛАУ".
q Определить матрицу, состоящую из коэффициентов левой части новой СЛАУ
q Матрицу, состоящую из коэффициентов левой части новой СЛАУ присвоим переменной Аxy.
q Определить вектор, состоящий из коэффициентов правой части новой СЛАУ
Элементы вектора содержат неизвестную переменную z, поэтому для определения этого вектора используем однострочную функцию с одним формальным аргументом (Вxy(z)). Некоторые сведения о пользовательских функциях можно найти в параграфе "Определение пользовательских функций".
4. Решить систему уравнений методом Крамера.
q Ввести сопроводительный текст в две строки "Решить систему уравнений методом Крамера" и "Дополнительные матрицы".
q Определить дополнительные матрицы в виде однострочных функций А1xy(z) и А2xy(z). Матрица А1xy(z) получается заменой первого столбца матрицы А вектором Вxy(z), а матрица А2xy(z) - заменой второго столбца матрицы А вектором Вxy(z).
Для получения матриц А1xy(z) и А2xy(z) использовать функцию чтения столбца матрицы (см. параграф "Верхний индекс и столбцы матрицы") и функцию augment(A,B) (см. параграф "Функции augment(A,B) и stack(A,B)") (см. Пример№3).
q Произвести символьный расчет функций А1xy(z) и А2xy(z). Некоторые сведения о пользовательских функциях можно найти в параграфе "Знак равенства в функциях и переменных MathCAD".
§ Для проведения символьных вычислений, например для функции А1xy(z), необходимо:
§ навести курсор на функцию А1xy(z) и щелкнуть левой кнопкой мыши,
§ манипулирую кнопками "стрелки" и "пробел" расположить синий угольник таким образом, что бы он охватывал левую часть функции (но не всю функцию), а угол синего уголка располагался справа ( ),
),
q нажать кнопку  в панели инструментов Math (Математический), а затем выбрать кнопку
в панели инструментов Math (Математический), а затем выбрать кнопку  в панелях инструментов Symbolic (Символьный).
в панелях инструментов Symbolic (Символьный).
q Аналогично произвести символьный расчет для функции А2xy(z).
Последовательность действий и расположение выражения на экране монитора приведена на Рис. 3.13.
q Ввести сопроводительный текст "Расчет неизвестных".
q Рассчитать две неизвестные, используя однострочные функции х(z) и y(z).
Для расчета функции х(z) необходимо найти частное от деления определителя функции А1xy(z) на определитель матрицы А.
В MatchCAD для этого необходимо: выбрать место для размещения выражения и нажать левую кнопку мыши (появится красный крестик), ввести мя функции – х(z) (нажать клавиши "х", "(", "z", ")"), ввести знак присвоения (клавиши "Shift"+":"), ввести имя функции А1xy(z), ввести функцию определителя (кнопки "Shift"+"|"), ввести знак деления (кнопка "/"), ввести имя матрицы А, ввести функцию определителя (кнопки "Shift"+"|"), произвести символьное вычисление функции.
q Аналогично определить неизвестную переменную y(z).
Последовательность действий и расположение выражения на экране монитора приведена на Рис. 3.13.
На Рис. 3.13 приведен листинг примера №9.
Пример №10
Задание. Найти базисные решения СЛАУ первым способом
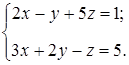
Решение системы имеет вид
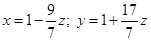
где 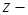 свободная переменная.
свободная переменная.
___________________________________________________
Определение для первого способа. Пусть СЛАУ является неопределенной и выделены базисные и свободные переменные. Базисным решением называется решение, полученное при нулевых значениях свободных переменных.

Рис. 3.13. Листинг программы MathCAD (Пример №9)
Базисных решений столько, сколько базисных миноров имеет СЛАУ.
Последовательность действий.
1. Ввести сопроводительный текст "Пример № 10" в правом верхнем углу листа.
2.Определить исходные данные для всех базисных миноров СЛАУ.
q Ввести сопроводительный текст "Исходные данные" в правом верхнем углу листа.
q Определить необходимые матрицы и векторы для всех базисных миноров.
Если х – свободный член, СЛАУ примет вид
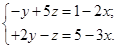
Если y – свободный член, СЛАУ примет вид
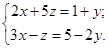
Если z – свободный член, СЛАУ примет вид
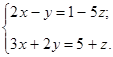
Проделать самостоятельно (см. Пример№9). Для убыстрения процесса использовать копирование и дальнейшее редактирование выражений. (см. параграф "Редактирование и манипулирование формулами")
Последовательность действий и расположение выражений на экране монитора приведена на Рис. 3.13.
4. Решить системы уравнений методом Крамера.
q Ввести сопроводительный текст в две строки "Решить систему уравнений методом Крамера" и "Дополнительные матрицы".
q Определить дополнительные матрицы в виде однострочных функций.
Проделать самостоятельно (см. Пример№9)
Последовательность действий и расположение выражения на экране монитора приведена на Рис. 3.16.
3. Рассчитать неизвестные для всех базисных решений.
q Ввести сопроводительный текст "Расчет неизвестных".
q Рассчитать неизвестные для всех базисных решений.
§ Написать однострочные функции х(z), y(z) и z(x).
Проделать самостоятельно (см. Пример№9).
Последовательность действий и расположение выражения на экране монитора приведена на.
5. Привести все базисные решения в виде матрицы
q Ввести сопроводительный текст "Базисные решения в виде матрицы".
q Формирование матрицы осуществить методом поэлементного определения матрицы (см. параграф "Поэлементное определение матрицы").
§ Определить первый элемент массива.
Для определения первого элемента матрицы надо сделать следующие операции: выбрать место для размещения выражения и нажать левую кнопку мыши (появится красный крестик), ввести имя матрицы – Mbaz (клавиши "Shift"+""m, "b", "a", "z"), ввести нижний индекс для задания элемента массива (клавиша "["), ввести индекс первого элемента массива (клавиши "0", ",", "0"), ввести знак присвоения (клавиши "Shift"+":"), ввести символ текстовой константы – парные кавычки (клавиши "Shift"+"""), ввести тактовую константу (между парных кавычек ввести букву - х).
Остальные элементы первой строки массива определить самостоятельно.
§ Определить первый элемент второй строки массива.
Для определения второго элемента второй строки матрицы надо сделать следующие операции: выбрать место для размещения выражения и нажать левую кнопку мыши (появится красный крестик), ввести имя матрицы – Mbaz (клавиши "Shift"+""m, "b", "a", "z"), ввести нижний индекс для задания элемента массива (клавиша "["), ввести индекс первого элемента массива (клавиши "1", ",", "1"), ввести знак присвоения (клавиши "Shift"+":"), ввести имя функции y1() (клавиши "y", "1", "(", ")"), ввести значение параметра функции (между круглыми скобками ввести цифру - 0).
Остальные элементы второй, третьей и четвертой строки массива заполнить самостоятельно.
Просмотреть содержимое массива Mbaz
§ Ввести имя массива и знак присвоения. На Рис. 3.14 приведен вид выражения.
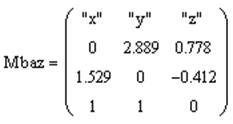
Рис. 3.14. Матрица с форматом представления чисел – General (Общий)
§ Отредактировать формат вывода данных
Последовательность операций: Вызвать диалоговое окно Result Format (Формат результата) вкладку Number Format (Формат числа) (навести курсор на матрицу и дважды щелкнуть левой кнопкой мыши), из списка Format (Формат) выбрать пункт Fraction (Дробь), закрыть диалоговое окно. В результате выражение примет вид, приведенный на Рис. 3.14.
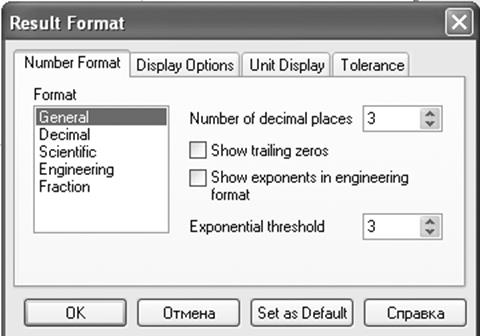
Рис. 3.15. Диалоговое окно Result Format (Формат результата) вкладка Number Format (Формат числа)
Последовательность действий и расположение выражения на экране монитора приведена на Рис. 3.16.
На Рис. 3.16 приведен листинг примера №10.


Рис. 3.16. Листинг программы MathCAD (Пример №10)
СОДЕРЖАНИЕ
1 Основы работы в MathCAD.. 1
1.1 Что такое MathCAD?. 1
1.2 Работа в MathCAD. 1
Знак равенства в функциях и переменных MathCAD.. 1
Ввод и размещение функций, переменных и пояснительного текста. 2
Определение и просмотр переменных, функций и сопроводительного текста. 3
Особенности ввода формул. 5
Редактирование и манипулирование формулами. 6
2 Массивы в Mathcad. 9
2.1 Использование шаблона для создания массива. 9
Создание матрицы-шаблона. 9
Редактирование элементов в матрице-шаблоне. 11
Поэлементное определение матрицы.. 11
Нижние индексы и элементы матрицы и вектора. 11
Верхний индекс и столбцы матрицы.. 12
2.2 Создание новых матриц из существующих массивов. 13
Функции augment(A,B) и stack(A,B). 13
Функция submatrix(A,ir,jr,ic,jc). 13
2.3 Обработка массивов. 13
Функции определения следа и ранга матрицы.. 13
Элементарные матричные вычисления. 15
3 Исследование систем линейных алгебраических уравнений в пакете MathCAD.. 22
Пример №1. 22
Пример №2. 26
Пример №3. 30
Пример №4. 32
Пример №5. 33
Пример №6. 35
Пример №7. 37
Пример №8. 39
Пример №10. 46
Date: 2015-07-02; view: 1363; Нарушение авторских прав