Краткая теория

Лабораторная задача QM-3

Дифракция потока частиц на двух щелях.

Краткая теория.

Волновые свойства микрочастиц наиболее отчетливо проявляются в явлении дифракции. Своеобразие свойств микрообъектов обнаруживается в следующем эксперименте. На диафрагму D с двумя узкими щелями направ-им параллельный пучок электронов, обладающих одинаковой кинетической

энергией (рис. 3.1). Если закрыть вторую щель, то распределение интенсивн-

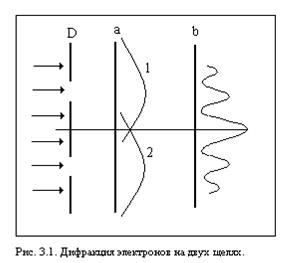ости свечения на флюоресцирующем экране будет соответствовать кривой 1 рис.3.1а. Если же закрыть первую щель и открыть вторую, то характер расп- ределения интенсивности свечения будет соответст-вовать кривой 2. Наконец, если открыть обе щели, то картина свечения флюоре-сцирующего экрана будет соответствовать кривой b на рис. 3.1. Она аналогич-на картине, получающей-ся при интерференции двух когеррентных свето-вых волн и отнюдь не эквивалентна наложению двух первых картин. Характер этой картины говорит о том, что на движение кажлого электрона оказывают влияние обе щели. Это естественно, так как электрон как бы “размазан” в пространстве и обладает волновы-ми свойствами. Расчеты показывают, что длина волны электронных волн соответствует формуле де Бройля:

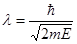, (3.1)

где Е – энергия электронов, а m – их масса.

Решение модельной задачи о дифракции электронов на двух щелях при-ведено ниже. Пусть поток электронов с энергией Е падает на непрозрачную диафрагму сдвумя щелями. Ширина каждой щели а, а расстояние между ще-

лями равно d. На расстоянии L от диафрагмы расположен экран, в плоско-

сти которого и наблюдается дифракционная картина. При анализе движения

частицы в пространстве между экранами исходят из уравнения Шредингера:

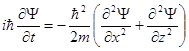. (3.2)

Решение уравнения (3.2) ищут в виде произведения двух функций:

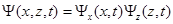. (3.3)

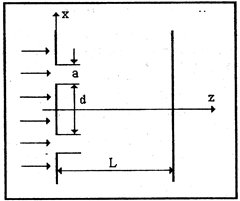
Рис 3.2. Схема модельного эксперимента по дифракции электронов.

Подставляя разложение (3.3) в уравнение (3.2), после несложных преобра-зований получим:

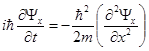, (3.4)

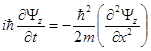. (3.5)

Движение частицы вдоль осей x и z происходит независимо.

Волновые функции в начальный момент времени выберем в виде

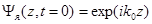, (3.6)

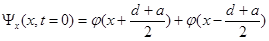. (3.7)

Первая из этих функций представляет собой плоскую волну с импульсом 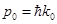. Такое состояние можно интерпретировать как однородный поток частиц, движущихся в пространстве вдоль оси z. Волновая функция 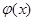, определяющая начальное состояние частицы, задает вероятность обнаружить частицу на каждой из щелей. Предполагается, что размер области, где 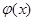отлична от нуля, составляет ≈ 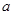. Предполагается, что дифракция потока частиц на двух щелях может быть рассмотрена как результат интерференции двух волновых пакетов, локализованных в начальный момент времени в областях вблизи 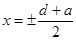. В случае, если ширина каждой из щелей значительно меньше расстояния между ними, в начальный момент времени пакеты не перекрываются и интерференция отсутствует. Однако с течением времени пакеты расплываются, что приводит к появлению интерференции. Одновременно с расплыванием происходит движение потока частиц вдоль оси z. Поэтому интерференционная картина, получающаяся в момент време-ни t, может быть зарегистрирована на экране, отстоящем на расстояние L от плоскости, в которой расположены щели.

Поскольку уравнение Шредингера является линейным, решение задачи (3.4) с начальным условием (3.7) можно представить в виде суперпозиции двух функций:

, (3.8)

удовлетворяющих уравнению Шредингера с граничными условиями:

;

.

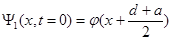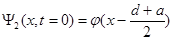Таким образом, волновые функци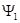и и 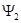описывают движение частицы, если открыта только первая или только вторая щель соответственно.

Плотность вероятности обнаружить частицу в каком-либо месте экрана определяется как

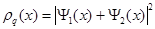, (3.9)

т. е. необходимо сложить сначала амплитуды вероятностей попадания в данную точку частиц, прошедших через первую и вторую щель, а затем вы-числить квадрат модуля полученного выражения. С точки зрения классичес-кой механики следовало бы сначала сложить вероятности попадания в точку x частиц, прошедших через обе щели:

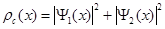. (3.10)

Результат будет иным, даже если эти вероятности вычислять по законам кван-товой механики.

В качестве иллюстрации сказанного рассмотрим случай 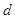» 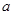, когда функ-ция 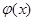может быть аппроксимирована - функцией:

;

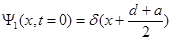. (3.11)

Для решения уравнения (3.4) с граничными условиями (3.11) воспользуемся результатами, полученными при изучении движения свободной частицы (см. задачу QM-1). Представим решение в виде:

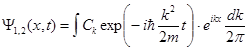, (3.12)

где коэффициенты 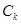определяются из начальных условий:

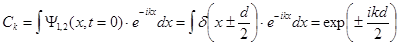. (3.13)

Как видно, для всех 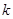. Это естественно, так как, выбирая волно-вой пакет сильно локализованным в координатном пространстве, мы одно-временно делокализуем его в пространстве импульсов. Подставив (3.13) в (3.12), получим:

, (3.14)

Учитывая, что 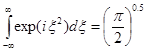, получим

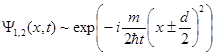. (3.15)

Тогда

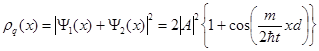; (3.16)

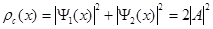, (3.17)

где 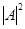- вероятность обнаружить частицу на экране в некоторой точке при одной открытой щели.

Как видно, в квантовом случае возникает интерференция, так что в некот-орых точках 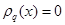, а в некоторых 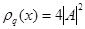. Таким образом, при двух открытых щелях происходит не удвоение (как естественно ожидать с классической точки зрения), а учетверение вероятности обнаружить частицу. Учитывая, что в рассматриваемом случае вдоль оси z существует стациона-рный поток частиц со скоростью , перепишем выражение (3.16)

в виде 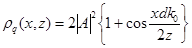, (3.18)

где z – расстояние от плоскости, в которой расположены щели, до плоскости экрана. Как видно из (3.18), на экране возникает система светлых и темных полос – интерференционная картина. При этом условие минимума интенсив-ности: 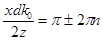, где 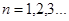, и в случае 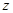» 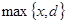, может быть записано в виде:

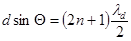, (3.19)

где 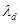- длина волны де Бройля, а 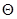- направление на 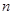- ый минимум.

Date: 2015-07-01; view: 357; Нарушение авторских прав