
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Из теории вероятностей и математической статистики
|
|
Событие – всякий факт, который в результате опыта может произойти или не произойти.
Если в результате опыта непременно должно появиться хотя бы одно из нескольких данных событий, то эти события образуют полную группу событий.
Суммой нескольких событий А 1, А 2, А З,..., Аn называется событие В, состоящее в появлении хотя бы одного из этих событий:
B = А 1 + А 2 + А З+…+ Аn (П.4.1)
Произведением нескольких событий А 1, А 2, А З,..., Аn называется событие С, состоящее в совместном появлении всех событий:
С = А 1 А 2 А 3... Аn. (П.4.2)
Каждому случайному событию А поставлено в соответствие неотрицательное число Р (А), называемое его вероятностью.
Вероятность события представляет собой численную меру степени объективной возможности (частоты) появления этого события.
За единицу измерения принимают вероятность достоверного события. Все другие события - возможные, но не достоверные - будут характеризоваться вероятностями, меньшими единицы, составляющими какую-либо долю единицы.
Вероятность события А, вычисленная при условии, что имело место другое событие В, называется условной вероятностью события А и обозначается как
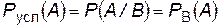 . (П.4.З)
. (П.4.З)
Теорема сложения вероятностей: для произвольных событий А и В вероятность суммы этих событий выражается формулой
 . (П.4.4)
. (П.4.4)
Теорема умножения вероятностей: вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое имело место:
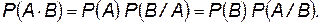 (П.4.5)
(П.4.5)
Из этой теоремы вытекают два следствия:
- если событие А не зависит от события В, то событие В не зависит от события А;
- вероятность произведения двух независимых событий равна произведению вероятностей этих событий.
Формула полной вероятности: если событие В может осуществляться с одним из n несовместимых событий А 1, А 2,..., Аn, образующих полную группу и обычно называемых гипотезами, то полная вероятность события В определяется формулой
 . (П.4. 6)
. (П.4. 6)
Формула Бернулли: если произошло последовательно n независимых опытов, в каждом из которых событие А может произойти с одной и той же вероятностью q, то вероятность того, что событие А произойдет ровно т раз, определяется по формуле Бернулли или по биноминальному распределению
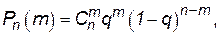 (П.4.7)
(П.4.7)
где
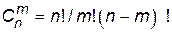 . (П.4.8)
. (П.4.8)
Случайной величиной X называется величина, которая в результате опыта может принять то или иное значение, причем неизвестно заранее, какое именно.
Дискретная случайная величина - величина, принимающая только отделенные друг от друга значения, которые можно заранее перечислить.
Непрерывная случайная величина - величина, возможные значения которой непрерывно заполняют некоторый промежуток.
Если дискретная случайная величина X примет значения 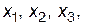
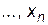 с заданными вероятностями
с заданными вероятностями 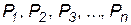 , то соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями, называется законом распределения.
, то соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями, называется законом распределения.
Непрерывная случайная величина имеет бесчисленное множество возможных значений, сплошь заполняющих некоторый промежуток. А так как сумма вероятностей отдельных значений случайной величины равна единице, то вероятность каждого значения должна стремиться к нулю. Поэтому вводится другая количественная характеристика - функция распределения, показывающая не вероятность события 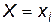 как закон распределения, а вероятность события Х < х, где х - некоторая текущая переменная:
как закон распределения, а вероятность события Х < х, где х - некоторая текущая переменная:
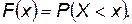 (П.4.9)
(П.4.9)
Функция F (x) существует как для дискретных, так и непрерывных случайных величин. Ее свойства:
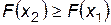 при
при 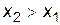 ; (П.4.10)
; (П.4.10)
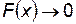 при
при 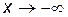 ; (П.4.11)
; (П.4.11)
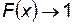 при
при 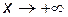 ; (П.4.12)
; (П.4.12)
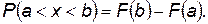 (П.4.13)
(П.4.13)
Плотность распределения
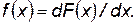 (П.4.14)
(П.4.14)
Элемент вероятности dP - вероятность того, что случайная величина X попадает на интервал dx около значения х:
 . (П. 4.15)
. (П. 4.15)
Наибольшее применение в практических задачах надежности находят показательные (экспоненциальные) и нормальные теоретические функции распределения для непрерывных случайных величин и закон Пуассона для дискретных случайных величин.
Показательное (экспоненциальное) распределение имеет следующий вид:
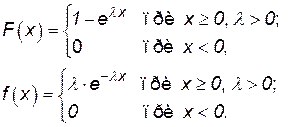 (П.4.16)
(П.4.16)
Нормальное распределение таково:
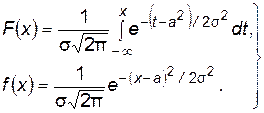 (П.4.17)
(П.4.17)
Значения функций (П.4.17) при а = 0 и s = 1 приведены в табл. П 3.1 и П 3.2.
Закон Пуассона позволяет определить вероятность того, что случайная величина, значениями которой могут быть только целые неотрицательные числа, примет определенное значение:
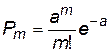 . (П.4.18)
. (П.4.18)
Математическое ожидание (среднее значение) случайной величины X, принимающей дискретные значения 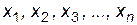 , с вероятностями
, с вероятностями 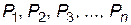 определяется как
определяется как
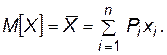 (П.4.19)
(П.4.19)
Для непрерывной случайной величины математическое ожидание определяется как
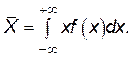 (П.4.20)
(П.4.20)
Таким образом, имеем:
для экспоненциального распределения
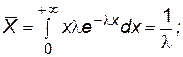 (П.4.21)
(П.4.21)
для нормального распределения
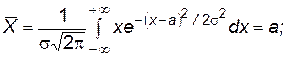 (П.4.22)
(П.4.22)
для закона Пуассона
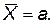 (П.4.23)
(П.4.23)
Основные свойства математического ожидания следующие:
• математическое ожидание постоянной С равно этой же постоянной
М [ С ] = С; (П.4.24)
• постоянный множитель выносится за знак математического ожидания
М [ СХ ] = СМ [ Х ], (П.4.25)
• математическое ожидание суммы любых случайных величин (как угодно связанных) равно сумме их математических ожиданий
M [ X + Y ] = M [ X ] + M [ Y ]; (П.4.26)
• математическое ожидание произведения независимых случайных величин равно произведению их математических ожиданий
M [ XY ] = M [ X ] M [ Y ]. (П.4.27)
Дисперсия определяется как математическое ожидание квадрата уклонения случайной величины от ее математического ожидания
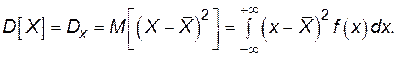 (П.4.28)
(П.4.28)
Дисперсия:
• экспоненциального распределения
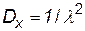 ; (П.4.29)
; (П.4.29)
• нормального распределения
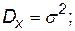 (П.4.30)
(П.4.30)
• закона Пуассона
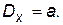 (П.4.31)
(П.4.31)
Основные свойства дисперсии:
• дисперсия постоянной С
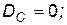 (П.4.32)
(П.4.32)
• постоянный множитель выходит за знак дисперсии в квадрате
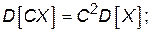 (П.4.ЗЗ)
(П.4.ЗЗ)
• дисперсия суммы попарно независимых случайных величин равна сумме дисперсии слагаемых:
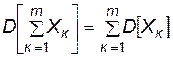 (П.4.34)
(П.4.34)
Среднеквадратичное отклонение случайной величины определяется как
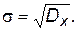 (П.4.35)
(П.4.35)
Если произведена серия из n независимых опытов, в каждом из которых могло появиться или не появиться некоторое событие А, то отношение числа опытов m, в которых появилось событие А, к общему числу произведенных опытов называется частотой события А или статистической вероятностью события А:
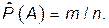 (П.4.36)
(П.4.36)
Оценку математического ожидания, удовлетворяющего условию состоятельности и несмещенности, можно произвести по формуле
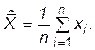 (П.4.37)
(П.4.37)
Дисперсия, удовлетворяющая этим же условиям, оценивается по формуле
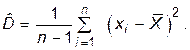 (П.4.38)
(П.4.38)
Центральная предельная теорема позволяет сформировать закон распределения случайной величины, которая может быть представлена как сумма других величин. Если исследуемая случайная величина может быть дана в виде суммы достаточно большого числа независимых или слабо независимых (либо слабо зависимых) элементарных слагаемых, каждое из которых в отдельности сравнительно мало влияет на сумму, то закон распределения этой случайной величины приближается к нормальному при увеличении числа слагаемых.
Практически центральной предельной теоремой можно пользоваться и тогда, когда имеет место сумма сравнительно небольшого числа случайных величин. Опыт показывает, что когда число слагаемых порядка десяти (а часто и меньше), закон распределения суммы обычно может быть заменен нормальным.
Квантиль – одна из числовых характеристик распределения вероятностей. Для действительной случайной величии Х с функцией распределения 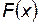 квантилью порядка р, o< p <1, называется число
квантилью порядка р, o< p <1, называется число 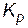 такое, что
такое, что 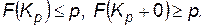 Если
Если 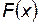 – непрерывная строго монотонная функция, то
– непрерывная строго монотонная функция, то 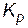 - единственное решение уравнения
- единственное решение уравнения 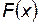 = р, т.е.
= р, т.е. 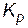 – функция р, обратная
– функция р, обратная 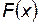 . Если
. Если 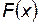 непрерывна и
непрерывна и 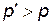 , то вероятность неравенства
, то вероятность неравенства 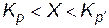 равна
равна 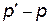 . Квантиль
. Квантиль 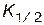 есть медиана случайной величины Х. Квантили
есть медиана случайной величины Х. Квантили 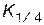 и
и 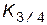 называются квартилями, а
называются квартилями, а 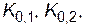
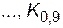 – децилями. Знание квантили для подходяще выбранных значений р позволяет составить представление о виде функции распределения.
– децилями. Знание квантили для подходяще выбранных значений р позволяет составить представление о виде функции распределения.
Например, для нормального распределения график функции распределения можно вычертить по децилям: 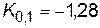 ;
; 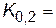 -0,84;
-0,84; 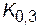 =
=
=– 0,52;  -0,25;
-0,25; 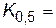 0;
0; 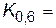 0,25;
0,25; 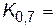 0,52;
0,52; 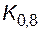 =0,84;
=0,84; 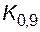 =1,28.
=1,28.
Квартили нормального распределения равны: 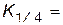 0,67;
0,67; 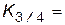 0,67.
0,67.
Date: 2015-06-11; view: 420; Нарушение авторских прав