Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Расчет коэффициента ассоциации
|
|
| Критерий | Лучшие | Отчисленные | Сумма (Νχ) |
| I | α = 75 | b= 16 | a +b = 91 |
| IV | с= 14 | d= 68 | c + d=82 |
| Сумма (Nv) | а + с = 89 | b + d = 84 | N= 173 |
Рассмотрим пример вычисления коэффициента ассоциации при изучении связи между такими критериями пригодности, как 1 и IV группы, и критериями успешности обучения – лучшие и отчисленные:
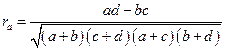
где а, b, с, d– численности альтернативных признаков (практически неограничены).
В корреляционной решетке (табл. 10) приведены исходные данные для расчетов (х– группа; у – успешность обучения).
Подставляя в формулу соответствующие значения из таблицы, находим величину коэффициента ассоциации (ra = 0,65), который выражается в долях от 0 до 1. Достоверность оценивается по его отношению к средней ошибке, определяемой по формуле
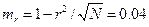откуда t= 16,25
Достоверность rа может быть определена также и по специальным таблицам [52].
При изучении корреляционной зависимости между вариационными рядами с отсутствием линейной зависимости более правомерным является вычисление корреляционного отношения, которое измеряет состояние любых, в том числе и нелинейных, связей между признаками.
В отличие от коэффициента корреляции, изучающего двустороннюю связь между x и у, корреляционное отношение (η) показывает только зависимость изменений второго (у) признака от изменений первого (х), или наоборот Корреляционное отношение – величина относительная, положительная и принимает значение от 0 до 1. Показатели корреляционного отношения обычно не равны между собой – ηy/x ≠ ηx/y Они определяются по следующим формулам:
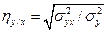и 
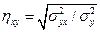, где 
– среднее квадратическое отклонение частотных или групповых средних величин (ух), то есть частная дисперсия;
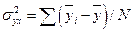– общая дисперсия совокупности.
Эти формулы можно выразить и в другом виде:
; 
; 
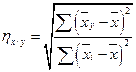
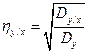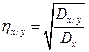
По приведенным формулам удобно определять коэффициенты корреляционного отношения для небольших выборок, а при наличии большого числа наблюдений необходимо предварительно весь материал группировать в вариационные ряды и вносить в корреляционную таблицу.
Рассмотрим вычисление корреляционного отношения на выборке из 10 наблюдений (табл. 11)
Сначала находим коэффициент корреляционного отношения полетов у по грубым ошибкам х, то есть η /х, для чего ранжируем выборку по x (значения x расположены в возрастающем порядке сверху вниз). Затем определяем вспомогательные величины для вычисления корреляционного отношения по x и подставляем в формулу, откуда ηγ/χ = 0,99.
Таблица11
Date: 2015-07-01; view: 447; Нарушение авторских прав