Алгебра событий

Пожалуйста, запомните ВАЖНЕЙШЕЕ ПРАВИЛО, без которого освоить тервер просто нереально:

Операция сложения событий означает логическую связку ИЛИ,
а операция умножения событий – логическую связку И.

1) Суммой двух событий и 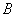называется событие которое состоит в том, что наступит или событие или событие 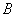или оба события одновременно. В том случае, если события несовместны, последний вариант отпадает, то есть может наступить или событие или событие .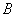

Правило распространяется и на бОльшее количество слагаемых, например, событие состоит в том, что произойдёт хотя бы одно из событий 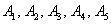, а если события несовместны – то одно и только одно событие из этой суммы: или событие 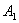, или событие 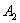, или событие 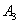, или событие 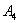, или событие .

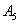Примеров масса:

События 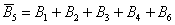(при броске игральной кости не выпадет 5 очков) состоит в том, что выпадет или 1, или 2, или 3, или 4, или 6 очков.

Событие 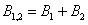(выпадет не более двух очков) состоит в том, что появится 1 или 2 очка.

Событие 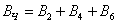(будет чётное число очков) состоит в том, что выпадет или 2 или 4 или 6 очков.

Событие 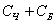заключается в том, что из колоды будет извлечена карта красной масти (черва или бубна), а событие 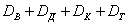– в том, что будет извлечена «картинка» (валет или дама или король или туз).

Чуть занятнее дело с совместными событиями:

Событие 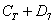состоит в том, что из колоды будет извлечена трефа или семёрка или семёрка треф. Согласно данному выше определению, хотя бы что-то – или любая трефа или любая семёрка или их «пересечение» – семёрка треф. Легко подсчитать, что данному событию соответствует 12 элементарных исходов (9 трефовых карт + 3 оставшиеся семёрки).

Событие 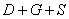состоит в том, что завтра в 12.00 наступит ХОТЯ БЫ ОДНО из суммируемых совместных событий, а именно:

– или будет только дождь / только гроза / только солнце;
– или наступит только какая-нибудь пара событий (дождь + гроза / дождь + солнце / гроза + солнце);
– или все три события появятся одновременно.

То есть, событие 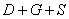включает в себя 7 возможных исходов.

Второй столп алгебры событий:

2) Произведением двух событий и 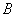называют событие 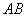, которое состоит в совместном появлении этих событий, иными словами, умножение 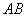означает, что при некоторых обстоятельствах наступит и событие , и событие 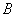. Аналогичное утверждение справедливо и для бОльшего количества событий, так, например, произведение 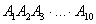подразумевает, что при определённых условиях произойдёт и событие 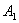, и событие 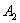, и событие 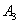, …, и событие .

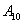Рассмотрим испытание, в котором подбрасываются две монеты и следующие события:

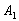– на 1-й монете выпадет орёл;
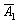– на 1-й монете выпадет решка;
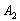– на 2-й монете выпадет орёл;
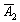– на 2-й монете выпадет решка.

Тогда:
– событие 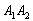состоит в том, что на обеих монетах (на 1-й и на 2-й) выпадет орёл;
– событие 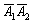состоит в том, что на обеих монетах (на 1-й и на 2-й) выпадет решка;
– событие 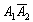состоит в том, что на 1-й монете выпадет орёл и на 2-й монете решка;
– событие 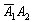состоит в том, что на 1-й монете выпадет решка и на 2-й монете орёл.

Нетрудно заметить, что события 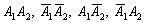несовместны (т.к. не может, например, выпасть 2 орла и в то же самое время 2 решки) и образуют полную группу (поскольку учтены все возможные исходы броска 2-х монет). Давайте просуммируем данные события: 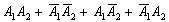. Как интерпретировать эту запись? Очень просто – умножение означает логическую связку И, а сложение – ИЛИ. Таким образом, сумму 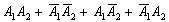легко прочитать понятным человеческим языком: «выпадут два орла или две решки или на 1-й монете выпадет орёл и на 2-ой решка или на 1-ой монете выпадет решка и на 2-й монете орёл»

Это был пример, когда в одном испытании задействовано несколько объектов, в данном случае – две монеты. Другая распространенная в практических задачах схема – это повторные испытания, когда, например, один и тот же игральный кубик бросается 3 раза подряд. В качестве демонстрации рассмотрим следующие события:

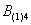– в 1-м броске выпадет 4 очка;
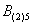– во 2-м броске выпадет 5 очков;
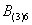– в 3-м броске выпадет 6 очков.

Тогда событие 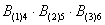состоит в том, что в 1-м броске выпадет 4 очка и во 2-м броске выпадет 5 очков и в 3-м броске выпадет 6 очков. Очевидно, что в случае с кубиком будет значительно больше комбинаций (исходов), чем, если бы мы подбрасывали монету.

…Понимаю, что, возможно, разбираются не очень интересные примеры, но это часто встречающиеся в задачах вещи и от них никуда не деться. Помимо монетки, кубика и колоды карт вас поджидают урны с разноцветными шарами, несколько анонимов, стреляющих по мишени, и неутомимый рабочий, который постоянно вытачивает какие-то детали =)

Date: 2015-07-01; view: 380; Нарушение авторских прав