
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Реферат
По дисциплине: Геодезические измерения
На тему:
«Геометрия земного эллипсоида»
Работу принял:
Потапова Н.Н
Оценка:
Работу сдал:
Шальнова В.О
ПГС-31
Москва 2014
Знание фигуры и размеров Земли требуется не только для геодезии и картографии, но и для многих отраслей знаний: космонавтики, авиации, мореплавания, астрономии, геологии, геофизики и др.
Поверхность Земли общей площадью 510 млн км2 разделяется на Мировой океан — 71 % и сушу — 29 %. Так как поверхность Мирового океана составляет 3/4 всей поверхности Земли, можно принять ее за фигуру Земли, а формы суши и дна океана изучать относительно поверхности Мирового океана. Поверхность, совпадающая со средним уровнем воды Мирового океана в спокойном состоянии, получила название основной уровенной поверхности.
Направления отвесных линий пересекают уровенную поверхность во всех ее точках под прямым углом, поэтому она всюду горизонтальна. Эта поверхность является также непрерывной, замкнутой, всюду выпуклой.
Фигура Земли, образованная уровенной поверхностью, совпадающей с поверхностью Мирового океана в состоянии полного покоя и равновесия и продолженная под материками, получила название геоида.
Таким образом, фигура геоида определяется направлением отвесных линий, положение которых зависит от распределения масс внутри Земли. Вследствие неизвестного и неравномерного распределения масс внутри Земли поверхность геоида является весьма сложной и математически неопределенной. Наиболее близкой к геоиду математической поверхностью является эллипсоид вращения.
 Земной эллипсоид
Земной эллипсоид
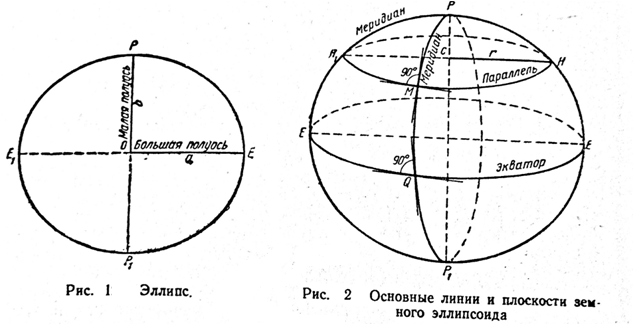
Для обработки геодезических измерений в единой обширной территории системе координат поверхность геоида заменяют математической поверхностью эллипсоида вращения, наиболее близкого по своей форме и размерам к геоиду. Этот эллипсоид вращения называется земным эллипсоидом или также сфероидом. Таким образом, поверхность эллипсоида является той координатной основой, без знание элементов которой задача определения координат опорных точек, расположенных на обширной территории, не может быть разрешена достаточно точно и правильно. Земной эллипсоид — геометрически правильное тело, образованное вращением эллипса РЕ1 Р1 Е (рис. 1) вокруг его малой оси РР1.
Полуоси земного эллипсоида, центр земного эллипсоида.
 Концы малой оси эллипсоида Р и Р1 называются полюсами, один из которых Р —северный, а другой Р1 — южный. Малая ось эллипсоида одновременно является геометрической осью вращения Земли, а центр эллипсоида О — центром ее тяжести. Большую полуось эллипсоида ОЕ обозначают через a, а малую ОР — через b.
Концы малой оси эллипсоида Р и Р1 называются полюсами, один из которых Р —северный, а другой Р1 — южный. Малая ось эллипсоида одновременно является геометрической осью вращения Земли, а центр эллипсоида О — центром ее тяжести. Большую полуось эллипсоида ОЕ обозначают через a, а малую ОР — через b.
Экватор.
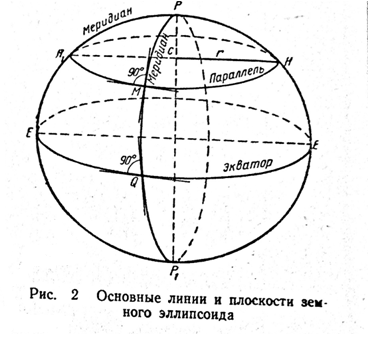
Плоскость EQE (рис. 2), проходящая через центр эллипсоида перпендикулярно к его оси вращения, называется плоскостью экватора, а сечение этой плоскостью поверхности эллипсоида — экватором. Очевидно, что экватор — это окружность, радиус которой равен большой полуоси ОЕ = a.
Параллель.
Сечения поверхности эллипсоида плоскостями, параллельными плоскости экватора и следовательно, перпендикулярными к оси вращения), называются параллелями. Параллели — также окружности определенного радиуса r. (Рис. а) 
Меридианные плоскости, меридианы.
Плоскости, проходящие через ось вращения эллипсоида, называются меридианными плоскостями, а сечения этими плоскостями поверхности эллипсоида называются меридианными сечениями или просто меридианами. Меридианные плоскости перпендикулярны к плоскости экватора; следовательно, касательные к экватору и меридианам в точках их пересечения перпендикулярны между собой. Также перпендикулярны между собой и касательные к меридианам и параллелям в точках их пересечений. (Рис. б)
Нормаль к поверхности земного эллипсоида, её свойства
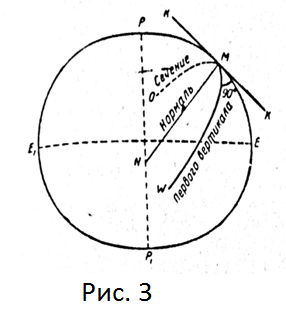 Если через точку М. (рис. 3) на поверхности эллипсоида провести касательную плоскость КК, то прямая MN, проходящая через данную точку перпендикулярно к плоскости КК, называется нормалью к поверхности эллипсоида в этой точке. Нормаль к поверхности эллипсоида всегда лежит в плоскости меридиана, проходящего через данную точку. Очевидно, что на экваторе нормаль лежит также и в плоскости экватора, а на полюсах она совпадает с осью вращения эллипсоида.
Если через точку М. (рис. 3) на поверхности эллипсоида провести касательную плоскость КК, то прямая MN, проходящая через данную точку перпендикулярно к плоскости КК, называется нормалью к поверхности эллипсоида в этой точке. Нормаль к поверхности эллипсоида всегда лежит в плоскости меридиана, проходящего через данную точку. Очевидно, что на экваторе нормаль лежит также и в плоскости экватора, а на полюсах она совпадает с осью вращения эллипсоида.
Всякая плоскость, проходящая через нормаль, называется нормальной, а сечение этой плоскостью поверхности эллипсоида — нормальным сечением. Любое другое сечение эллипсоида плоскостью, не проходящей через нормаль, называется наклонным, или косым сечением. Очевидно, что экватор и меридианы — нормальные, а параллели — наклонные сечения.
Нормальная плоскость, нормальное сечение.
Плоскость первого вертикала, сечение первого вертикала.
Нормальная плоскость, проходящая через данную точку М (рис. 3) перпендикулярно к плоскости меридиана, называется плоскостью первого вертикала, а сечение этой плоскостью поверхности эллипсоида — сечением первого вертикала.
Главные нормальные сечения.
Нормальное сечение поверхности S в данной её точке М — линия пересечения с плоскостью, проведённой через нормаль в точке М. С помощью Н изучается искривление поверхности S в различных (касательных) направлениях, выходящих из точки М. Среди этих направлений имеются два (взаимно перпендикулярных) главных направления, для которых нормальная кривизна (т. е. кривизна соответствующего Н) достигает наибольшего и наименьшего значений k 1 и k 2 (т.е. главные кривизны в данной точке). При этом кривизны Н берутся со знаком + или -, если направление вогнутости сечения совпадает (противоположно) с положительным направлением нормали к поверхности. Нормальные кривизны поверхности в произвольных направлениях весьма просто выражаются через главные кривизны. Именно, кривизна kn Н. с., проведённого в направлении, составляющем угол φ с первым из указанных выше главных направлений, связана с k 1 и k 2 соотношением (формула Эйлера):
kn = k 1 cos2 φ + k 2 sin2 φ.
С помощью кривизны Н изучаются также кривизны наклонных сечений поверхности. Именно, кривизна k наклонного сечения плоскостью α, проходящей через данную касательную прямую а, выражается формулой Менье:

где φ — угол между плоскостью α и нормалью к поверхности, k n — нормальная кривизна поверхности в направлении прямой а.
Так же меридианное сечение и сечение первого вертикала называются главными нормальными сечениями.
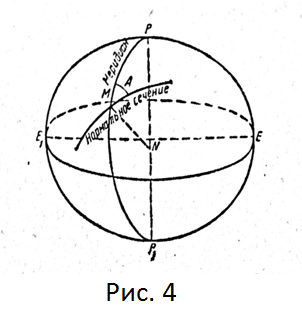
Геодезический азимут.
Взаимное положение меридиана и любого другого нормального сечения, проходящего через точку М (рис. 4) на данном меридиане, определяется на поверхности эллипсоида углом А, образованным данной нормальной плоскостью с плоскостью меридиана. Этот угол называется геодезическим азимутом.
Так же азимутом называется в геодезии угол между направлением на север (в Южном полушарии — на юг) и направлением на какой-либо удалённый предмет. Отсчитывается обычно по часовой стрелке.
При определении азимута по компасу необходимо вводить поправку на магнитное склонение, возникающее вследствие несовпадения географических и магнитных полюсов земли.
| Направление | Азимут в градусах |
| Север | 0° или 360° |
| Северо-восток | 45° |
| Восток | 90° |
| Юго-восток | 135° |
| Юг | 180° |
| Юго-запад | 225° |
| Запад | 270° |
| Северо-запад | 315° |
Движение по азимуту заключается в определении на местности нужного направления движения по данному азимуту и выдерживании этого направления при движении.
Радиус кривизны.
Через точку на поверхности эллипсоида можно провести бесконечное множество нормальных сечений, которые в разных направлениях будут иметь разную кривизну. Но для вычисления различных геодезических величин, связанных с кривизной поверхности эллипсоида, выделяются только два нормальных сечений, кривизну которых необходимо знать. Это главные нормальные сечения: меридиан и сечение первого вертикала. Кривизна их определяется радиусами кривизны, которые, по аналогии с соответствующими, нормальными сечениями носят название главных радиусов кривизны и обозначаются: радиус кривизны меридиана через М, а радиус кривизны первого вертикала — через N.
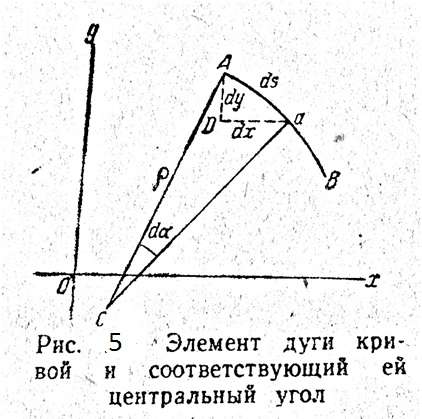
Определим радиус кривизны меридиана М.
Из математики известна, что кривизна любой плоской кривой АВ (рис. 5) определяется в общем виде формулой
ds=ρdα

Принимая кривую АВ за дугу меридиана, а элементы ds, ρ и dα кривой — соответственно за элементы ds, М и dB меридиана, данную формулу перепишем так:
ds=MdB
Если через точки A и а данной фигуры провести параллельно осям плоских координат прямые AD = dx и DA = dy, то из бесконечно малого треугольника AaD будем иметь
ds2=dx2+dy2
Отсюда пишем
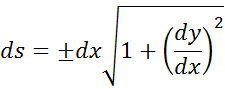
Учитывая предыдущие формулы, найдем после небольших преобразований

Откуда
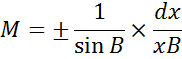
Дифференцируя выражение по В, получим
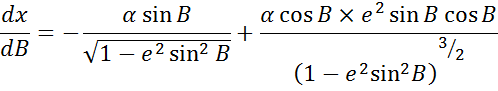
Или
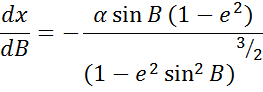
Подставим теперь значение этой производной в формулу. Так как величина М существенно положительная, то для радиуса кривизны меридиана получим окончательно
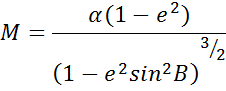
Формулу радиуса кривизны первого вертикала приведем без вывода

Сопоставляя эти формулы, замечаем, что
r=N cos B
Из формул видно, что радиусы кривизны М и N главных нормальных сечений увеличиваются с возрастанием широты В. Следовательно, кривизна этих сечений уменьшается с перемещением от экватора к полюсам.
Указанными формулами определяется также, что радиус кривизны меридиана М является наименьшим, а радиус кривизны первого вертикала N — наибольшим в данной точке. На полюсах М = N.
Первая величина. Вторая величина. Третья величина.
При вычислении некоторых геодезических величин поверхность эллипсоида заменяют поверхностью шара. В этом случае радиус шара берут равным среднему арифметическому из радиусов кривизны всех возможных нормальных сечений в данной точке. В окончательном виде средний радиус кривизны равен
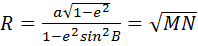
т. е. среднему геометрическому из радиусов кривизны главных нормальных сечений.
Радиусы кривизны М и N — основные элементы сфероидической геодезии, без которых вычисления многих геодезических величин на поверхности эллипсоида невозможны. В частности, радиус кривизны меридиана М необходим для вычисления длин дуг меридиана и разностей широт, а радиус кривизны первого вертикала N — для вычисления длин дуг параллелей, разностей долгот и сближений меридианов.
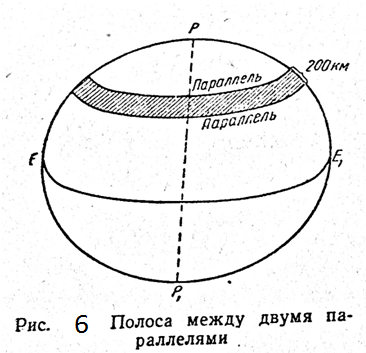
Средний радиус кривизны R используется в геодезии для вычисления сферических избытков треугольников, а также при замене некоторых частей поверхности эллипсоида поверхностью шара. Как показывают расчеты, такая замена практически не отражается на точности геодезических работ в пределах двухградусной (по широте) полосы, т.е. в пределах полосы шириной (между двумя параллелями) до 200 км (рис. 6).
Для величин М, N и R имеются специальные таблицы, в которых численные значения их даются в форме выражений

Здесь ρ" — число секунд в радиане, равное 206 265",806; как известно, число это вводится в вычисления для перевода угловых величин из градусной меры в аналитическую и наоборот.
Взаимные нормальные сечения.
В геодезии нормальным сечением эллипсоида (референц-эллипсоида или общеземного) называется линия пересечения поверхности эллипсоида плоскостью, проходящей через нормаль к поверхности эллипсоида в ее заданной точке. Нормальное в исходной точке 1 сечение, проходящее через точку 2, называется прямым нормальным сечением для точки 1 иобратным нормальным сечением для точки 2. Нормальное в точке 2 сечение, проходящее через точку 1, называется прямым нормальным сечением для точки 2 и обратным нормальным сечением для исходной точки 1. Совместно все эти нормальные сечения называются взаимными нормальными сечениями. Поскольку нормали к поверхности эллипсоида в точках 1 и 2 не параллельны, то и взаимные нормальные сечения не совпадают.
Азимут прямого нормального сечения представляет собой двугранный угол, образованный плоскостью геодезического меридиана исходной точки 1 и плоскостью, проходящей через нормаль к поверхности эллипсоида в исходной точке 1 и заданную точку 2. Азимут прямого нормального сечения отсчитывается от северного направления меридиана по ходу часовой стрелки от 0° до 360°.
Азимут A1,2 нормального в точке 1 (B1, L1) сечения, проходящего через точку 2 (B2, L2), может быть вычислен по следующим формулам, предложенным Б. С. Кузьминым:
m = (1 - e²) tg B2,
n = (e'² N1 sin B1) / (N2 sin B2),
ctg ω = m (1 + n),
p = ctg ω cos B1,
q = cos (L2 - L1) sin B1,
tg A1,2 = (sin (L2 – L1)) / (p - q).
В этих формулах:
B1, B2 и L1, L2 — географические (геодезические) широты и долготы точек;
N1 и N2 — длина нормалей к поверхности эллипсоида под широтами B1 и B2;
e² и e'² — квадраты эксцентриситета и второго эксцентриситета меридианного эллипса.
Формулы дают точное значение азимута прямого нормального сечения при любых расстояниях.
Геодезическая линия.
 Если на поверхности эллипсоида взять две точки: А и В (рис. 7), не лежащие на одной параллели и на одном меридиане, то нормали этих точек пересекутся с осью вращения эллипсоида РР1 в разных точках: нормаль точки А пересечет ось вращения в точке N1, а нормаль точки В — в точке N2. Следовательно, нормальная плоскость, проходящая через нормаль AN1 и точку В, и нормальная плоскость, проходящая через нормаль BN2 и точку А, не совпадают одна с другой и занимают в эллипсоиде разные положения. Пересечения этих плоскостей с поверхностью эллипсоида дадут соответственно и разные нормальные сечения, проходящие через одни и те же точки А и В: нормальное сечение АаВ — в точке А и обратное ему нормальное сечение ВbА — в точке В. Эти нормальные сечения, образующие между точками A и В узкий двуугольник (рис. 8), называются взаимными нормальными сечениями, из которых АаВ прямое нормальное сечение- в точке А, а ВbА - обратное нормальное сечение в той же точке А.
Если на поверхности эллипсоида взять две точки: А и В (рис. 7), не лежащие на одной параллели и на одном меридиане, то нормали этих точек пересекутся с осью вращения эллипсоида РР1 в разных точках: нормаль точки А пересечет ось вращения в точке N1, а нормаль точки В — в точке N2. Следовательно, нормальная плоскость, проходящая через нормаль AN1 и точку В, и нормальная плоскость, проходящая через нормаль BN2 и точку А, не совпадают одна с другой и занимают в эллипсоиде разные положения. Пересечения этих плоскостей с поверхностью эллипсоида дадут соответственно и разные нормальные сечения, проходящие через одни и те же точки А и В: нормальное сечение АаВ — в точке А и обратное ему нормальное сечение ВbА — в точке В. Эти нормальные сечения, образующие между точками A и В узкий двуугольник (рис. 8), называются взаимными нормальными сечениями, из которых АаВ прямое нормальное сечение- в точке А, а ВbА - обратное нормальное сечение в той же точке А.
Таким образом, если по измеренным углам составить треугольник ABC (рис. 9), то его стороны будут иметь двойственное значение как образованные не совпадающими между собой взаимными нормальными сечениями и, следовательно, создадут в построении этого треугольника некоторую неопределенность.
Взаимное положение прямого и обратного нормальных сечений зависит от расположения соединяемых ими конечных точек. Например, точке А (см. рис.7), расположенной южнее точки В, прямое нормальное сечение АаВ пройдет южнее обратного нормального сечения B bA; наоборот, в точке В, лежащей севернее точки А, прямое нормальное сечение ВbА пройдет севернее обратного нормального сечения АаВ. При положении точек на одном меридиане или на одной параллели взаимные нормальные сечения сливаются в одну линию.
В зависимости от расстояний между конечными точками угол Δ (рис.8), образованный взаимными нормальными сечениями, максимально достигает следующих величин:

и так далее.
 Как видно, при малых расстояниях, не превышающих 20—30 км, взаимные нормальные сечения расходятся на ничтожно малые углы, близкие к нулю. В таких случаях каждое прямое и обратное нормальное сечение принимают во всех построениях за одну кривую, соединяющую две точки на поверхности эллипсоида.
Как видно, при малых расстояниях, не превышающих 20—30 км, взаимные нормальные сечения расходятся на ничтожно малые углы, близкие к нулю. В таких случаях каждое прямое и обратное нормальное сечение принимают во всех построениях за одну кривую, соединяющую две точки на поверхности эллипсоида.
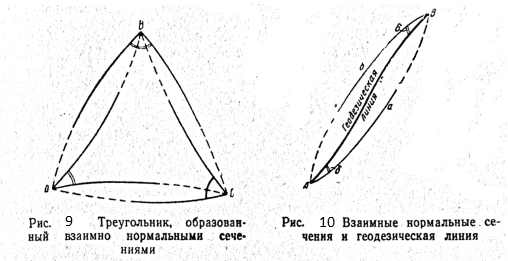
Но при значительных расстояниях между точками эти расхождения необходимо учитывать. Взаимные нормальные сечения заменяют в этом случае так называемой геодезической линией, представляющей собой кривую (рис. 9), по которой расположилась бы нить, туго натянутая между двумя точками на поверхности эллипсоида. Следовательно, она является линией кратчайшего расстояния между данными точками. Длина ее практически равна длине нормальных сечений и определяется по формуле

где σ"—центральный угол, выраженный в секундах, которому соответствует дуга s на поверхности, эллипсоида; N1 — радиус кривизны первого вертикала в точке А.
Геодезическая линия образует с нормальными сечениями вполне определенный угол о, который по величине равен приблизительно одной трети угла А. Положение геодезической, линии между нормальными сечениями схематически показано на рис. 10.
Date: 2015-07-01; view: 1742; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |