Следующая теорема утверждает, что ²жадный² алгоритм Краскала всегда приводит к остову минимального веса

Теорема 10.1. При i<n-1 граф Т_i+1 можно построить. Граф Т_n-1 является остовом минимального веса во взвешенном графе <G,w>.

Подграф Т_i имеет ровно i рёбер и n вершин и потому при i < n-1 является несвязным. А так как граф G связен, то в нём есть по крайнеё мере одно ребро, не составляющее циклов с рёбрами графа Т_i. Итак, нужное ребро e_i+1 существует и граф Т_i+1 можно построить.

Рассмотрим граф Т_n-1. Поскольку Т_n-1 является (n, n-1)-графом без циклов, то по теореме 9.1 является деревом. Докажем, что Т_n-1 - остов минимального веса. Предположим противное. Среди всех остовов графа G минимального веса выберем такой остов Т, который имеет с деревом Т_n-1 максимальное число общих рёбер. Пусть e i = (а,в) ребро дерева Т_n-1, не содержащееся в Т и имеющее минимальный номер среди рёбер дерева Т_n-1, не входящих в Т (в процессе построения дерева Т_n-1 его рёбра получили номера 1,2,…,n-1). В дереве Т есть простая (а,в)- цепь. Присоединив к ней ребро е_i, получим цикл. В этом цикле есть ребро е, не входящее в дерево Т_n-1 (иначе в Т_n-1 был бы цикл). Заменив в дереве Т ребро е на е_i, получим новый остов Т¢ = Т – е + е_i. Но Т - остов минимального веса, следовательно, w(Т^¢) = w(T) + w(ei) - w(e) ≥ w(T), т.е. w( e_i) ≥ w(e) (1). С другой стороны, присоединяя ребро е к Т_i-1 (при i=1 полагаем Т_i-1 = О_n), мы не получим цикла, поскольку рёбра е1,е2,…, е_i-1, е входят в дерево Т, и потому, если бы вес w(ei) был больше, чем w(e), мы взяли бы при построении дерева Тi ребро е вместо e_i. Из (1) теперь следует, что w(e_i)= w(e), w(Т¢)= w(Т).

Итак, Т' - остов минимального веса. Число рёбер, общих для деревьев Т' и Т_n-1, больше, чем число рёбер, общих для Т и Т_n-1, что противоречит выбору дерева Т. Полученное противоречие и доказывает теорему.

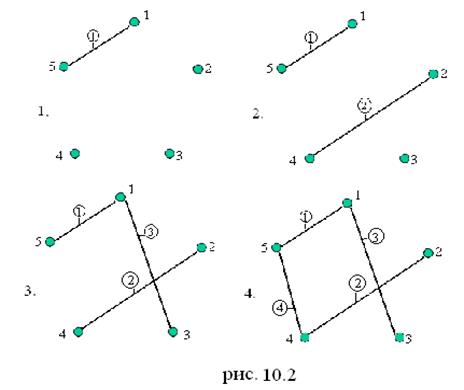
Теперь зная алгоритм, решим задачу. На каждом шаге будем строить ациклический подграф с 5 вершинами (n=5), значит будет n-1 = 4 шага (рис. 9.3). На первом шаге выбираем e₁ = (1,5), на втором - e₂ = (2,4), на третьем - e₃ = (1,3)

и на четвертом - e₄ = (5,4). Рёбра (1,5), (2,4), (1,3), (4,5) составляют остов минимального веса. Вес остова Т_n-1 равен:

w(Т_n--1) = 1+2+3+4 = 10. Таким образом, эта сеть дорог (рис.9.3 (4)) будет самой дешёвой и ее строительство обойдётся в 10 условных единиц.

Алгоритм Прима отличается от алгоритма Краскала только тем, что на каждом шаге строится не просто ациклический подграф, а дерево:

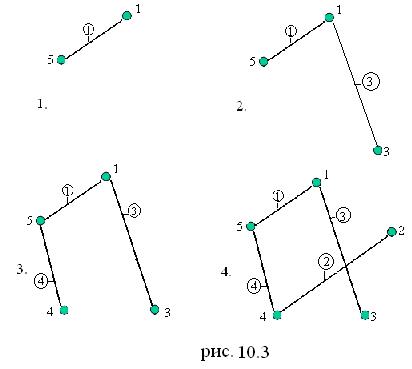
1. Выбираем ребро e₁ = (a,b) минимального веса и строим дерево D₁ = e₁.

2. Если дерево D_i, содержащее i ребер порядка i + 1, уже построено, и i < n - 1, то среди ребер, соединяющих вершины этого дерева с вершинами графа G, не входящими в D_i, выбираем ребро e_i+1 минимального веса и строим дерево D_{i+1 =} D_iÈ e_i+1 (рис.9.4).

Для алгоритма Прима также верна теорема 10.1.

Теорема. Алгоритм Краскала строит минимальный остов (n,m)-графа G за время O(m×n).

Доказательство: в алгоритме Краскала n - 1 шагов; на каждом шаге разыскивается ребро минимального веса из некоторого списка ребер, содержащего не более m ребер, поэтому число операций кратно m×n.