
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Метод обратной матрицы
|
|
Метод обратной матрицы (называемый также модифицированным симплексным методом) является еще одним численно реализуемым алгоритмом решения задач линейного программирования, основанным на общей схеме метода последовательного улучшения плана.
Напомним, что на каждой итерации метода последовательного улучшения плана решаются следующие системы линейных алгебраических уравнений:
§ система для вычисления базисных координат опорного плана 
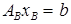 , (1)
, (1)
§ система для вычисления псевдоплана 
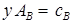 , (2)
, (2)
§ система для вычисления коэффициентов 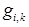 разложения вектора
разложения вектора 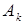 по базису
по базису
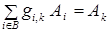 . (3)
. (3)
Решение этих систем составляет наиболее трудоемкий этап реализации метода последовательного улучшения плана.
Запишем систему (3) в векторно-матричном виде. Обозначив  , имеем
, имеем
 . (4)
. (4)
Так как 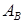 – базисная подматрица, то она
– базисная подматрица, то она
невырождена. Поэтому для нее существует обратная матрица 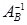 . Воспользуемся обратной матрицей для отыскания решений систем уравнений (1), (2), (4). Получим следующие равенства:
. Воспользуемся обратной матрицей для отыскания решений систем уравнений (1), (2), (4). Получим следующие равенства:
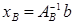 , (5)
, (5)
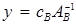 , (6)
, (6)
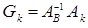 . (7)
. (7)
Использование формул (5) – (7) и лежит в основе алгоритма метода обратной матрицы.
Следующая теорема дает формулы для пересчета обратной матрицы при переходе к новому базису.
Теорема 1. Пусть 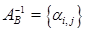 и
и 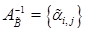 – две обратные матрицы, где
– две обратные матрицы, где 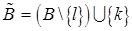 ; значения индексов
; значения индексов  и
и  получены по правилам метода последовательного улучшения плана. Тогда справедливы следующие равенства:
получены по правилам метода последовательного улучшения плана. Тогда справедливы следующие равенства:
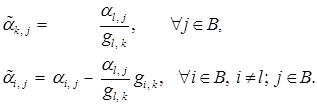 (7)
(7)
Формулы (7) выводятся аналогично формулам для пересчета симплексной таблицы (см. теорему 3.1).
Из формул (7) следует, что обратная матрица на каждой итерации вычисляется не по
определению, а из предыдущей обратной матрицы по тем же правилам, которые использовались и для пересчета симплексных таблиц.
Теперь мы можем сформулировать общую итерацию метода обратной матрицы. Предположим, что имеется некоторый допустимый базис 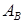 и соответствующий ему опорный план
и соответствующий ему опорный план  . Далее выполняются следующие действия:
. Далее выполняются следующие действия:
0. Вычисление обратной матрицы 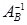 для исходного базиса.
для исходного базиса.
1. Нахождение опорного решения (псевдоплана)  , соответствующего базису
, соответствующего базису 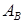 по формуле (6)
по формуле (6) 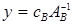 .
.
2. Проверка признака оптимальности. Для этого проверяется двойственная допустимость базиса, то есть выполнение неравенств
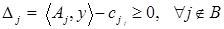 . (8)
. (8)
Если все неравенства (8) выполняются, то векторы  и
и  являются решениями, соответственно, прямой и двойственных задач линейного программирования. На этом работа метода прекращается.
являются решениями, соответственно, прямой и двойственных задач линейного программирования. На этом работа метода прекращается.
3. Выбор  . Положим
. Положим  :
:  .
.
4. Нахождение коэффициентов разложения вектора 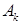 по базису:
по базису: 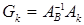 .
.
5. Построение 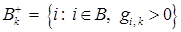 .
.
6. Если 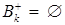 , то прямая задача линейного программирования не имеет решения в силу неограниченности целевой функции на допустимом множестве, а двойственная задача не имеет решения в силу пустоты допустимого множества. Работа метода прекращается.
, то прямая задача линейного программирования не имеет решения в силу неограниченности целевой функции на допустимом множестве, а двойственная задача не имеет решения в силу пустоты допустимого множества. Работа метода прекращается.
7. Выбор номера 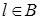 такого, что
такого, что
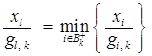 .
.
8. Построение нового базиса 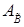 , где
, где 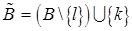 .
.
9. Пересчет обратной матрицы по формулам (7) и вычисление нового опорного плана  , соответствующего базису
, соответствующего базису 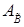 , по формулам (2.6).
, по формулам (2.6).
10. Замена базиса 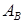 на
на 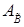 и матрицы
и матрицы 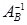 на
на 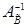 . Переход к следующей итерации, к первому ее этапу.
. Переход к следующей итерации, к первому ее этапу.
Метод обратной матрицы имеет ряд существенных преимуществ по сравнению с симплексным методом. Обратная матрица имеет меньшие размеры, чем симплексная таблица. Особенно это существенно, когда 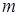 значительно меньше
значительно меньше 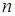 . На каждой итерации метода обратной матрицы в большей мере, чем в симплексном методе, используются данные исходной задачи линейного программирования. Поэтому в ходе большого количества итераций погрешности вычислений меньше
. На каждой итерации метода обратной матрицы в большей мере, чем в симплексном методе, используются данные исходной задачи линейного программирования. Поэтому в ходе большого количества итераций погрешности вычислений меньше
накапливаются, что приводит к большей устойчивости этого алгоритма по сравнению с симплексным методом.
Наконец, отметим, что для отыскания исходного допустимого базиса и соответствующего ему
опорного плана также возможно применение метода искусственного базиса в сочетании с методом обратной матрицы.
Date: 2015-06-12; view: 1930; Нарушение авторских прав