Метод искусственного базиса

Этот параграф посвящен приемам нахождения исходного допустимого базиса необходимого

для начала работы метода последовательного улучшения плана.

Пусть необходимо решить задачу линейного программирования в канонической форме записи

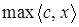
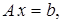(1)

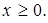
Предположим, не ограничивая общности, что все координаты вектора 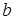неотрицательны. Метод искусственного базиса имеет две разновидности.

Рассмотрим так называемый двухфазный вариант метода искусственного базиса.

Первая фаза. Этот этап состоит в решении

вспомогательной задачи. Для ее построения вводятся переменные 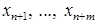, которые называются искусственными. Вспомогательная задача – это задача линейного программирования вида:

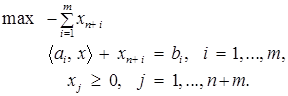(2)

Вспомогательная задача имеет следующие особенности.

1)_Задача (2) имеет решение при любой исходной задаче (1).

Обозначим 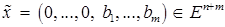. Оче-видно, что вектор удовлетворяет всем ограничениям задачи (2), то есть ее допустимая область непуста.

Далее, целевая функция ограничена сверху на допустимой области, так как в силу неотрицательности всех координат допустимого вектора

.

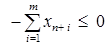2)_Легко увидеть, что вектор 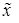является опорным планом задачи (2), его базис 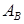состоит из искусственных векторов .

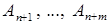Таким образом, выполняются все требования, позволяющие применить к задаче (2) симплексный метод. В результате получим оптимальный план 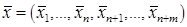и соответствующий ему базис 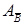вспомогательной задачи.

Вторая фаза. Начнем с анализарезультата, полученного на первой фазе. Возможны следующие случаи.

1) Среди искусственных координат вектора 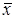имеются ненулевые (положительные), то есть найдется хотя бы один номер такой, что 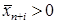. Тогда, очевидно, (максимальное значение целевой функции задачи (2) отрицательно). Убедимся, что в этом случае допустимая область исходной задачи пуста. Допустим, что 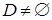. Тогда для любого 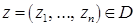вектор 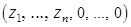является допустимым решением задачи (2), на котором значение целевой функции равно нулю. Полученное противоречие означает, что 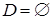, то есть исходная задача линейного программирования (1) не имеет решения. На этом вторая фаза заканчивается.

2) Все искусственные координаты вектора 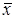небазисные (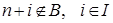). В этом случае вектор 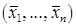, составленный из первых 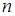координат вектора 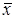, является опорным планом задачи (1) с базисом 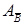. В этом случае вторая фаза заключается в решении задачи (1) симплексным методом, где в качестве исходного допустимого базиса используется .

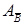3) Все искусственные координаты вектора 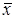нулевые (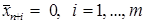), но среди них имеются базисные (то есть найдется хотя бы один номер 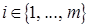такой, что 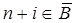). Чтобы воспользоваться этим опорным планом для решения исходной задачи симплексным методом, надо вывести эти искусственные векторы из базиса. Наличие нулевых базисных компонент означает, что построенный опорный план вырожден, а значит, ему соответствует несколько различных базисов. Значит, можно перейти к другому базису этого опорного плана, не содержащему искусственных векторов.

Пусть множества 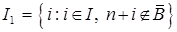и

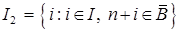составляют разбиение множества 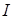. Запишем задачу линейного программирования, которая решается на второй фазе.

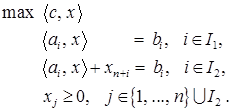(3)

Для применения к задаче (3) симплексного метода необходимо исключить из базиса 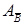оставшиеся искусственные векторы, после чего фактически решается исходная задача.

В заключение изложим так называемый однофазный вариант метода искусственного базиса. В нем вместо основной задачи (1) и вспомогательной задачи (2) решается следующая задача:

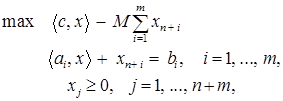(4)

где 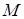– неопределенный положительный параметр. Эта задача в некотором смысле эквивалентна исходной задаче (1), так как она имеет следующие свойства.

1. Очевидно, что задача (4) всегда имеет допустимое решение (что устанавливается так же, как и для задачи (2)).

2. Задача (1) имеет решение тогда и только тогда, когда существуют значения параметра 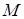такие, что задача (4) имеет решение, в котором все искусственные координаты равны нулю. Тогда если 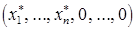– решение задачи (4), то вектор 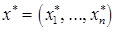– решение задачи (1).

3. Задача (1) не имеет решения в силу несовместности ограничений тогда и только тогда, когда существуют значения параметра 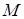такие, что задача (4) имеет решение, в котором некоторые искусственные координаты положительны.

4. Задача (1) не имеет решения в силу неограниченности целевой функции на допустимой области тогда и только тогда, когда для любых значений параметра 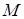задача (4) не имеет решения по той же причине.

Все эти утверждения легко проверяются.

Date: 2015-06-12; view: 1237; Нарушение авторских прав