Система уравнений Максвелла

Теперь можно все свойства (законы) магнитного и электрического полей записать в виде системы уравнений Максвелла. В дифференциальной форме:

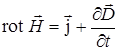(7.11) 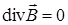(7.13);

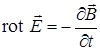(7.12) 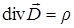(7.14).

Это полевые уравнения, применимые для описания электромагнитных явлений. В дополнение к ним следует записать материальные уравнения:

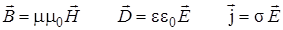. (7.15).

Уравнения Максвелла в виде (7.11-7.15) были записаны Хевисайдом. Считая математику “служанкой” техники, Хевисайд часто предлагал формулы без математического доказательства. Им же был разработан без строгого доказательства операторный метод; открыт слой Хевисайда, полностью отражающий короткие волны.

Обратим внимание на то, что уравнения (7.13) и (7.14) являются дифференциальным следствием (7.12), (7.11). Для доказательства применим операцию 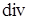к (7.12):

.

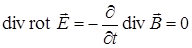Но так как 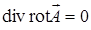, то 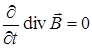, что совпадает с продифференцированным по времени уравнением (7.13).

Применим теперь операцию 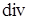к (7.11):

.

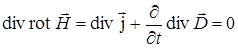Тогда 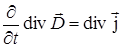. Учтем уравнение непрерывности:

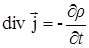
и получим: 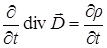и 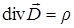, что совпадает с продифференцированным по времени уравнением (7.14).

Это означает, что система уравнений Максвелла не переполнена. В ней содержится 8 скалярных уравнений и 6 неизвестных компонент векторов 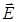и .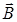

Физический смысл уравнений Максвелла:

- (7.11). Источником магнитного поля 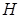являются ток проводимости и переменное электрическое поле.

- (7.12). Источником электрического поля 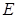являются неподвижные электрические заряды (при этом поле потенциально) и переменное магнитное поле (при этом электрическое поле является вихревым).

- (7.13). Не существует магнитных зарядов; силовые линии магнитного поля являются замкнутыми; поле является вихревым.

- (7.14). Потенциальное электрическое поле имеет источником неподвижные заряды, силовые линии вектора электрического смещения начинаются на 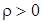и заканчиваются на зарядах .

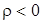Уравнения Максвелла и материальные уравнения дополняются формулой для плотности энергии электромагнитного поля:

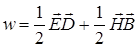. (7.16)

Date: 2015-06-11; view: 518; Нарушение авторских прав