Обзор существующих численных методов решения задачи

Среднеквадратическое приближение функции

Постановка задачи

Разработать схему алгоритма и написать программу на языке Turbo Pascal 7.0 для выполнения среднеквадратического приближения функции, заданной в узлах.

Математическая формулировка задачи

Пусть имеется множество функций 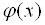, принадлежащих линейному пространству функций. Под близостью в среднем интерполируемой и интерполирующей функций будем понимать результат оценки интеграла

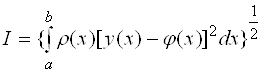, (3.1)

где 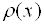- весовая функция.

Такое приближение называют среднеквадратичным.

Обзор существующих численных методов решения задачи

Задача среднеквадратичного приближения возникает во многих областях прикладных исследований, например, при статистической обработке данных эксперимента с использованием регрессивного анализа, при оценивании параметров моделей, в задачах фильтрации и т.п.

Когда уровень неопределенности в задании приближаемой функции f(x_i), i=1..m, достаточно велик, что характерно для обработки экспериментальных данных, бессмысленно требовать выполнения условий интерполирования; кроме того, число точек задания функции f(x_i) часто весьма велико. Все это делает применение интерполирования мало перспективным по причинам плохой обусловленности задачи высокой размерности и проблем сходимости процесса интерполяции

Одной из наиболее простых и, поэтому, широко используемых приближающих функций является алгебраический полином

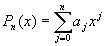
Метод среднеквадратичного приближения обеспечивает построение полинома Pn(x), исходя из минимизации величины

Рассмотренный метод приближения минимизирует среднеквадратичное уклонение аппроксимирующего полинома от аппроксимируемой функции, но не гарантирует от значительных локальных ошибок. Для предотвращения подобной возможности используют полиномы наилучшего равномерного приближения.

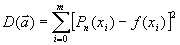
в пространстве параметров a₀ , a₁ ,...,a_n. Существуют различные подходы к решению задачи минимизации функции D(a). Простейший из них приводит к необходимости решения нормальной системы линейных алгебраических уравнений

Однако, уже при n > 5 матрица такой системы оказывается настолько плохо обусловленной, что полученные из (3.4) значения a_jоказываются мало пригодными для вычисления P_n(x). Поэтому, при необходимости построения полиномов наилучшего среднеквадратичного приближения более высоких степеней применяют другие алгоритмы, например, метод сингулярного разложения.

4. Численный метод решения задачи
Можно рассмотреть две задачи:

1 - подобрать функцию 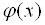так, чтобы выполнялось неравенство

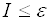; (3.5)

2 - найти наилучшее приближение, т.е. такую функцию 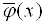, чтобы было справедливым соотношение

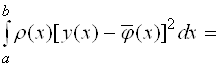
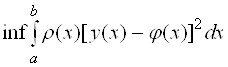. (3.6)

Далее займемся отысканием наилучшего приближения.

Разложим функцию 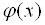по системе линейно независимых функций :

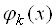. (3.7)

В дальнейшем для сокращения записи будем пользоваться определением скалярного произведения в пространстве функций :

.

Подставляя (3.7) в условие (3.6), получим

.

Дифференцируя это выражение по и приравнивая производные нулю, получим

. (3.8)

Определитель этой системы есть определитель Грама функций 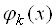. В силу их линейной независимости этот определитель не равен нулю. Следовательно, из системы (3.8) можно найти коэффициенты , определяющие функцию 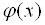согласно (3.6) и минимизирующие интеграл от погрешности . Таким образом, наилучшее среднеквадратичное приближение существует и оно единственно.

При использовании ортонормированной системы функций 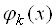система (3.8) упрощается:

,

т.е. являются коэффициентами Фурье, а наилучшее приближение есть ряд Фурье, обрываемый на каком-то члене.

Доказано, что в любом линейно нормированном пространстве при линейной аппроксимации вида (3.4) наилучшее приближение существует, хотя оно может быть не единственным.

В тех случаях, когда функции 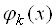не ортогональны, при 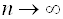определитель Грама уменьшается, приближаясь к нулю. Тогда система становится плохо обусловленной и ее решение дает большую погрешность. В этой ситуации обычно берут не более пяти-шести членов в сумме (3.7).

В качестве 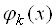чаще всего используют полиномы Лежандра, Чебышева, Лагерра, Эрмита, ортогональные с заданным весом.

Рассмотрим частный случай, когда необходимо найти наилучшее приближение функции, заданной таблично. Для вещественных функций, заданных на конечном множестве точек, скалярное произведение определяется формулой

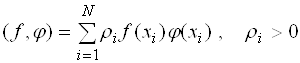, (3.9)

где - число заданных узлов.

Условие наилучшего среднеквадратичного приближения записывается следующим образом:

. (3.10)

Полагая , где 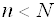, и подставляя этот многочлен в (3.10), придем к системе (3.8), в которой скалярные произведения вычисляют согласно (3.9). Описанная процедура аппроксимации носит название метода наименьших квадратов.

Наиболее употребительный вариант метода наименьших квадратов соответствует случаю степенного вида функций 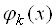, т.е. 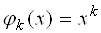, причем .

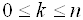Система уравнений (3.8) при этом принимает вид

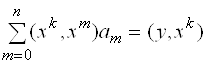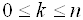, , (3.11)

где .

5. Схема алгоритма

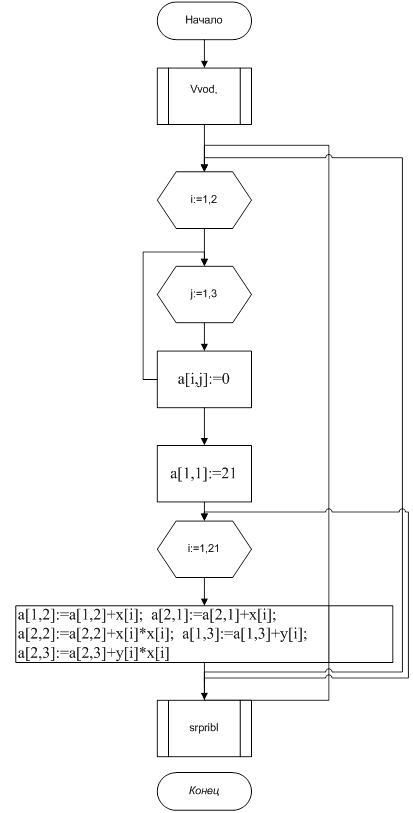
Рис. 3.1 Основная программа

Рис. 3.2 Процедура ввода данных

Рис 3.3 Процедура среднеквадратичного приближения

6. Текст программы

program srpribl; {$R+}

uses graph;

label 1,2,3,4;

const м=2;

type mas= array [1..21] of real;

mas1= array [1..м] of real;

mas2= array [1..м,1..м+1] of real;

var i,j:byte;

у1,x1:mas;

xx1:mas1;

a1:mas2;

procedure vvod (x,у: mas);

begin

x[1]:=0;у[1]:=0.290234387293458; x[2]:=0.25;у[2]:=0.201247759722173;

x[3]:=0.5;у[3]:=0.0712686786428094;x[4]:=0.75; у[4]:=0.044294935464859;

x[5]:=1;у[5]:=-0.0745576142333448; x[6]:=1.25;у[6]:=-0.0807833694852889;

x[7]:=1.5;у[7]:=-0.233371530473232;x[8]:=1.75;у[8]:=-0.283957027737051;

x[9]:=2;у[9]:=-0.308697660081089;x[10]:=2.25;у[10]:=-0.42091366359964;

x[11]:=2.5;у[11]:=-0.516991161741316;x[12]:=2.75;у[12]:=-0.427710095947851;

x[13]:=3;у[13]:=-0.374748698528856;x[14]:=3.25;у[14]:=-0.229905794281513;

x[15]:=3.5;у[15]:=-0.205365492492496639;x[16]:=3.75;у[16]:=-0.129155068378896;

x[17]:=4;у[17]:=-0.0438349825330079;x[18]:=4.25;у[18]:=0.0294586319476366;

x[19]:=4.5;у[19]:=0.132592592108995;x[20]:=4.75;у[20]:=0.206369574274868;

x[21]:=5;у[21]:=0.26959548862651;

end;

procedure srpribl (xx:mas1;a:mas2);

var l:real;

s,z,к1:integer;

begin

for s:=1 to м-1 do

for z:=s+1 to м do

begin

a[z,s]:=-a[z,s]/a[s,s];

for к1:=s+1 to м+1 do a[z,к1]:=a[z,к1]+a[z,s]*a[s,к1]

end;

xx[м]:=a[м,м+1]/a[м,м]; writeln(' xx[',м,']=',хх[м]:2:3);

for i:=м-1 downto 1 do

begin

l:=a[i,м+1];

for j:=i+1 to м do l:=l-xx[j]*a[i,j];

xx[i]:=l/a[i,i]; writeln(' xx[',i,']=',xx[i]:2:3)

end

end;

procedure Grafik (var x,у:mas;xx:mas1)

var ec,gd,gm:integer;

begin

gd:=detect;

initgraph (gd,gm,' ');

ec:=graphresult;

if ec<>grok then begin

writeln ('Oshibka v inicializacii grafika');

halt (1);

end;

setcolor(white);

line (0,420,620,420);

line (0,0,0,420);

setcolor (white);

for i:=1 to 21 do begin

circle (round (x[i]*150),round (у[i]*100),1);

end;

setcolor (yellow);

for i:=1 to м do begin

circle (round (x[i]*150),round (xx[i]*100),1);

end;

setcolor (green);

for i:=2 to м do begin

line (round (x[i-1]*150),round(xx[i-1]*100),round (x[i]*150),

round (xx[i]*100));

end;

end;

begin

vvod(x1,у1);

for i:=1 to 2 do

for j:=1 to 3 do a[i,j]:=0;

a[1,1]:=21;

for i:=1 to 21 do

begin

a[1,2]:=a[1,2]+x[i];

a[2,1]:=a[2,1]+x[i];

a[2,2]:=a[2,2]+x[i]*x[i];

a[1,3]:=a[1,3]+у[i];

a[2,3]:=a[2,3]+у[i]*x[i]

end;

srpribl(xx1,a1);

for i:=1 to 21 do

writeln(у[i]:2:3,' ',xx[1]+xx[2]*x[i]:2:3);

Grafik(x1,у1,хх1);

end.

Date: 2015-06-11; view: 689; Нарушение авторских прав