
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Решение. Выбор рационального проекта (стратегии, альтернативы) осуществляется с использованием различных критериев для оптимизации решений в условиях
|
|
Выбор рационального проекта (стратегии, альтернативы) осуществляется с использованием различных критериев для оптимизации решений в условиях неопределенности.
Разработкой рекомендаций для выбора наилучшего варианта действий в условиях неопределенности занимается теория статистических решений. Эта математическая теория рассматривает игры с природой, в которых под природой понимаются объективные обстоятельства, внешняя среда. Считается, что природа сознательно не противодействует игроку. Условие задачи представлено в виде матрицы выигрышей (aji) игры с природой:
Матрица игры 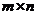
| Si xj | |||
xj – стратегии сознательного игрока, 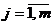 ;
;
Si – состояния природы,  ;
;
aji – выигрыш сознательного игрока при использовании им стратегии xj, если состоянием природы будет Si.
1. Критерий Лапласа
Данный критерий предполагает равновероятность состояний внешней среды и рекомендует выбор стратегии с максимальным средним выигрышем:
КЛ =  .
.
Вероятности состояний природы Si равны между собой:
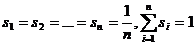 .
.
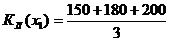 = 177;
= 177;
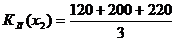 = 180;
= 180;
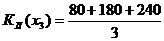 = 167;
= 167;
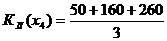 = 157.
= 157.
Следовательно, по критерию Лапласа рациональным будет производство при 4 АРМ.
2. Критерий Байеса
Этот критерий учитывает вероятности состояний природы и рекомендует выбор стратегии с максимальным среднеожидаемым выигрышем:
КБ = 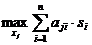 ,
, 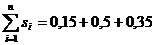 = 1.
= 1.
 = 61;
= 61;
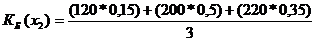 = 65;
= 65;
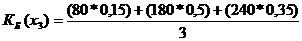 = 62;
= 62;
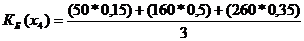 = 60.
= 60.
Следовательно, по критерию Байеса рациональным будет производство при 4 АРМ.
3. Критерий Вальда (максиминный критерий, критерий крайнего пессимизма, критерий наибольшей осторожности).
Данный критерий ориентируется на худшее состояние внешний среды и рекомендует выбор стратегии с максимальным гарантированным выигрышем в таких условиях:
КВ = 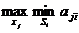 .
.
Кв = 50.
Следовательно, по критерию Вальда рациональным будет производство при 8 АРМ и потока заказов на обслуживание = 10.
4. Критерий Сэвиджа (минимаксного риска).
Критерий минимаксного риска ориентируется на самую неблагоприятную обстановку и рекомендует выбор стратегии с минимальным риском:
КС = 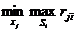 .
.
Для использования данного критерия необходимо перейти от матрицы выигрышей к матрице рисков.
Риск (rji) – разность между выигрышем, который игрок получил бы, если бы он знал, что состоянием природы будет состояние Si, и выигрышем, который игрок получит, не имея этой информации при использовании стратегии xj:
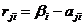 ,
, 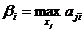 (при заданном i).
(при заданном i).
Кс = 200.
Следовательно, по критерию Сэвиджа рациональным будет производство при 4 АРМ и потока заказов на обслуживание = 30.
5. Критерий Гурвица (компромиссный критерий, критерий пессимизма-оптимизма).
Этот критерий учитывает индивидуальные предпочтения сознательного игрока к пессимизму и оптимизму. Для его использования необходимо задать значение коэффициента пессимизма α, α 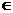 [0,1]:
[0,1]:
КГ = 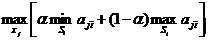 .
.
КГ (х1) = 0,4*150 + (1-0,4)*200 = 180;
КГ (х2) = 0,4*120 + (1-0,4)*220 = 180;
КГ (х3) = 0,4*80 + (1-0,4)*240 = 176;
КГ (х4) = 0,4*50 + (1-0,4)*260 =176.
Следовательно, по критерию Гурвица рациональным будет производство при 4 АРМ.
Таким образом, рационально создание сервисного центра по обслуживанию и сопровождению своих изделий при АРМ = 4 и потоком заказов на обслуживание = 20.
Date: 2015-07-17; view: 629; Нарушение авторских прав