
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Обработка результатов эксперимента на основе регрессии
|
|
Часто целью исследования является определение функциональной связи между факторами и откликом (реакцией модели) по данным, полученным при экспериментах с моделью объекта или непосредственно с объектом. Такая цель достигается регрессионным анализом значений факторов 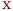 и отклика
и отклика 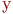 .
.
Под регрессией в теории вероятностей и математической статистике понимают зависимость среднего значения какой-либо величины от некоторой другой (других) величины. Регрессионный анализ - это совокупность методов построения и исследования регрессионной зависимости между величинами (в нашем случае между факторами и откликом) по статистическим данным. Статистические данные накапливаются при проведении эксперимента.
Формальная схема эксперимента выглядит так (рис. 5.6).
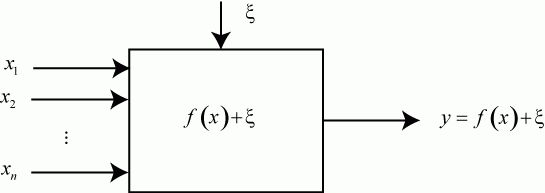
Рис. 5.6. Формальная схема эксперимента
Прямоугольник представляет исследуемый объект или его математическую модель. Обозначения на рис. 5.6:
 - значения факторов,
- значения факторов, 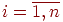 ;
;
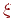 - случайный фактор, помеха. Будем считать, что эта случайная величина имеет нормальное распределение с матожиданием
- случайный фактор, помеха. Будем считать, что эта случайная величина имеет нормальное распределение с матожиданием 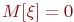 . Влияние помехи на отклик аддитивное, то есть ее случайные значения прибавляются к значениям отклика;
. Влияние помехи на отклик аддитивное, то есть ее случайные значения прибавляются к значениям отклика;
 - искомая функциональная зависимость между факторами и откликом.
- искомая функциональная зависимость между факторами и откликом.
Отклик 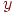 - величина случайная.
- величина случайная. 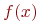 представляет собой среднее значение отклика (так как
представляет собой среднее значение отклика (так как 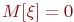 ):
): 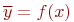 .
.
Исследуемый объект представляется как "черный ящик", никаких предположений о виде функции  нет. Поэтому представим ее в виде аппроксимирующего полинома:
нет. Поэтому представим ее в виде аппроксимирующего полинома:
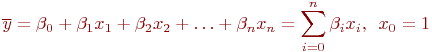
Этот полином получил название уравнения регрессии, а коэффициенты 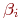 - коэффициенты регрессии. От точности подбора коэффициентов регрессии зависит точность представления
- коэффициенты регрессии. От точности подбора коэффициентов регрессии зависит точность представления  .
.
Коэффициенты 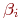 определяются путем обработки полученных в ходе эксперимента варьируемых значений факторов и откликов.
определяются путем обработки полученных в ходе эксперимента варьируемых значений факторов и откликов.
Однако из-за ограниченного числа наблюдений точные значения 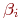 получить нельзя, будут найдены их оценки
получить нельзя, будут найдены их оценки 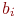 :
:
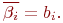
Поэтому уравнение регрессии принимает вид:
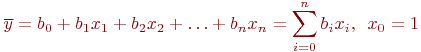
Вообще-то метку над 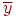 теперь надо бы изменить, так как вместо
теперь надо бы изменить, так как вместо 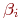 в уравнении теперь стоят
в уравнении теперь стоят 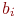 , но мы этого делать не будем, чтобы не загромождать изложение новыми значками.
, но мы этого делать не будем, чтобы не загромождать изложение новыми значками.
В уравнении регрессии могут участвовать и так называемые "совместные эффекты" (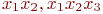 и т. п.) или степени значений факторов (
и т. п.) или степени значений факторов (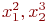 и т. п.). Совместные эффекты и степени факторов можно обозначать обобщенным фактором. Например, уравнение регрессии
и т. п.). Совместные эффекты и степени факторов можно обозначать обобщенным фактором. Например, уравнение регрессии
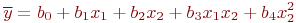
можно представить так:
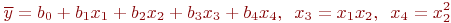
Итак, для определения выражения 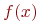 надо:
надо:
- выбрать степень аппроксимирующего полинома - уравнения регрессии;
- определить коэффициенты регрессии.
Выбор уравнения регрессии обычно начинают с линейной модели. Например, для двухфакторного эксперимента ее вид:
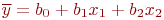
Если окажется, что такая аппроксимация дает неприемлемые отклонения при сравнении с экспериментальными точками отклика y, то модель усложняется, например, так:
 или
или
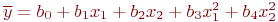 и т.д.
и т.д.
Коэффициенты регрессии 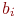 для выбранного уравнения определяются из условия минимума суммы квадратов ошибок, вычисленных по все экспериментальным точкам. Это делается так. Введем обозначения:
для выбранного уравнения определяются из условия минимума суммы квадратов ошибок, вычисленных по все экспериментальным точкам. Это делается так. Введем обозначения:
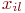 - значение
- значение 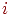 -го фактора в наблюдении номер
-го фактора в наблюдении номер 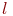 ;
;
 - значение отклика в
- значение отклика в 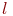 -м наблюдении;
-м наблюдении;
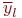 - значение отклика, вычисленное по принятому уравнению регрессии и данным
- значение отклика, вычисленное по принятому уравнению регрессии и данным 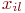 .
.
Очевидно, сумма квадратов ошибок между экспериментальными значениями  и вычисленными по уравнению регрессии
и вычисленными по уравнению регрессии  для всех
для всех  наблюдений равна:
наблюдений равна:
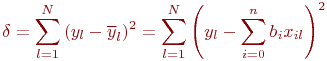
Для определения минимума ошибки? возьмем частные производные от 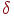 по всем неизвестным коэффициентам регрессии
по всем неизвестным коэффициентам регрессии 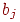 ,
, 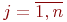 и приравняем их нулю:
и приравняем их нулю:
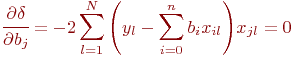
Нетрудно убедиться, что это условие минимума, а не максимума. Очевидно:
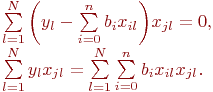
Для лучшей наглядности выделим неизвестные коэффициенты регрессии и получим:
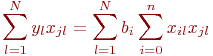
Выражение (5.3) представляет собой систему из  уравнений для нахождения
уравнений для нахождения  неизвестных коэффициентов регрессии
неизвестных коэффициентов регрессии 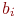 , которые окончательно определят выбранное уравнение регрессии.
, которые окончательно определят выбранное уравнение регрессии.
Нахождение коэффициентов регрессии справедливо при следующих допущениях:
- Случайный фактор
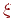 имеет нормальное распределение с матожиданием
имеет нормальное распределение с матожиданием 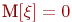 .
. - Результаты наблюдений
 - независимые нормально распределенные случайные величины. Если это не соблюдается, то следует измерять другой отклик, удовлетворяющий этому условию, но функционально связанный с исследуемым откликом
- независимые нормально распределенные случайные величины. Если это не соблюдается, то следует измерять другой отклик, удовлетворяющий этому условию, но функционально связанный с исследуемым откликом 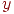 .
. - Точность наблюдений (количество реализаций модели) не меняется от наблюдения к наблюдению.
- Точность наблюдения
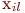 должна быть выше точности
должна быть выше точности  .
.
Пример 5.8. На модели объекта проведен однофакторный эксперимент из пяти наблюдений, результаты которого сведены в таблицу (табл. 5.10).
Найти функциональную связь фактора с откликом 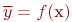 .
.
| Таблица 5.10. Результаты эксперимента | |||||||
| Фактор и отклики | Наблюдение | 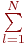
| |||||
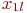
| 0,5 | 1,0 | 1,5 | 2,0 | |||

| 7,0 | 4,8 | 2,8 | 1,4 | |||
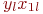
| 2,4 | 2,8 | 2,1 | 7,3 |
Решение
Примем, что кроме управляемого фактора 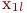 при проведении эксперимента на объект воздействует случайный фактор, распределенный по нормальному закону с математическим ожиданием
при проведении эксперимента на объект воздействует случайный фактор, распределенный по нормальному закону с математическим ожиданием 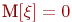 . Также предположим, что эта связь - линейная, следовательно, уравнение регрессии нужно определять в виде:
. Также предположим, что эта связь - линейная, следовательно, уравнение регрессии нужно определять в виде:
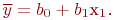
Неизвестных коэффициентов два: 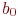 и
и 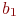 . Запишем (5.3) в виде двух уравнений для
. Запишем (5.3) в виде двух уравнений для 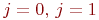 и в каждом из них разложим суммы по индексу
и в каждом из них разложим суммы по индексу 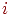 :
:
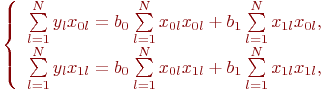
Так как 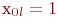 , получим:
, получим:
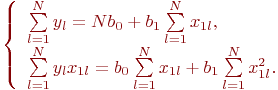
Подставим данные эксперимента из табл. 5.10 в систему (5.4):
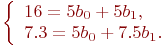
Решим систему из двух уравнений и получим: 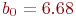 ,
, 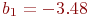 .
.
Следовательно, искомое уравнение регрессии:
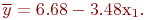
Доверительные границы для истинных значений 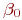 и
и 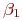 примера 5.8 определяются как обычно:
примера 5.8 определяются как обычно:
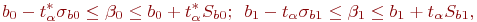
где 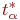 - аргумент распределения Стьюдента;
- аргумент распределения Стьюдента; 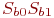 - среднеквадратические отклонения величин
- среднеквадратические отклонения величин 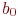 и
и 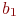 соответственно.
соответственно.
Значения 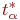 определяются из таблицы распределения Стьюдента для
определяются из таблицы распределения Стьюдента для 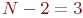 степеней свободы и задаваемом уровне достоверности
степеней свободы и задаваемом уровне достоверности 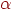 . Пусть
. Пусть 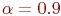 , тогда
, тогда 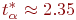 .
.
Значения 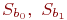 находятся по формулам:
находятся по формулам:
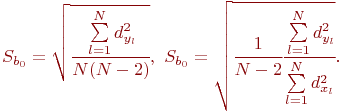
Данные для вычисления  ,
, 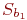 представлены в табл. 5.11.
представлены в табл. 5.11.
| Таблица 5.11. Данные для вычисления S_b0, S_b1 | |||||||
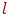
| 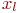
| 
| 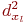
| 
| 
| 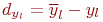
| 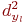
|
| 1,0 | 1,0 | 7,0 | 6,68 | -0,32 | 0,1024 | ||
| 0,5 | 0,5 | 0,25 | 4,8 | 4,94 | 0,14 | 0,0196 | |
| 1,0 | 2,8 | 3,2 | 0,40 | 0,16 | |||
| 1,5 | -0,5 | 0,25 | 1,4 | 1,46 | 0,06 | 0,0036 | |
| 2,0 | -1,0 | 1,0 | 0,28 | 0,28 | 0,0784 |
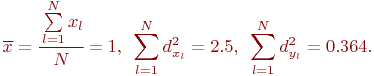
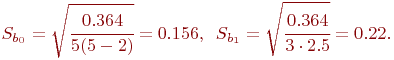
С уровнем достоверности 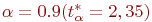
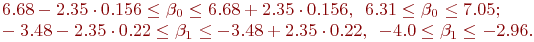
Большой размах доверительных границ объясняется малым числом наблюдений в данном эксперименте.
Доверительные границы для y принимают разные значения в зависимости от значений факторов [33].
На практике часто ограничиваются обобщенными оценками адекватности построенной модели: величиной среднего абсолютного отклонения
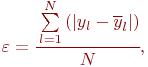
или (и) величиной среднеквадратической ошибки на единицу веса
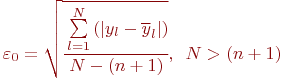
Весом или степенью свободы эксперимента называют разность  между числом наблюдений
между числом наблюдений  и числом коэффициентов регрессии
и числом коэффициентов регрессии 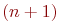 .
.
Предположим, что линейная модель 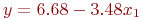 недостаточно точно отображает связь между фактором
недостаточно точно отображает связь между фактором 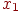 и откликом
и откликом 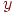 .
.
Введем в рассмотрение более сложную нелинейную модель:
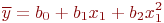
Для определения коэффициентов регрессии 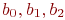 обозначим
обозначим 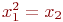 и получим двухфакторную линейную модель:
и получим двухфакторную линейную модель:
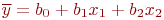
В этом случае уравнение (5.3) раскрывается так:
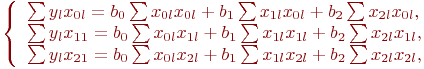
В уравнениях принято: 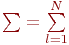
Так как 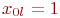 ,
, 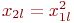 , то система принимает вид:
, то система принимает вид:
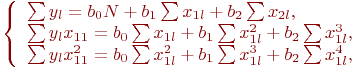
Подставим значения фактора и отклика из табл. 5.10:
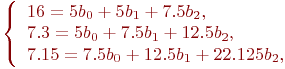
Решим систему из трех уравнений с тремя неизвестными и получим: 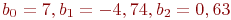 .
.
Таким образом, получено новое уравнение регрессии:
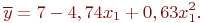
По значениям 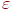 и
и 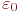 нетрудно убедиться в том, что нелинейная модель более точно отображает моделируемый процесс (см. табл. 5.10), чем линейная.
нетрудно убедиться в том, что нелинейная модель более точно отображает моделируемый процесс (см. табл. 5.10), чем линейная.
В рассмотренном примере ошибка модели определялась по тем же данным, по которым и была определена сама модель. Однако при сокращенных планах экспериментов (см. п. 4.3) можно выполнить все или часть "сэкономленных" наблюдений для получения так называемых проверочных данных, которые и использовать для вычисления ошибки 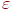 или
или 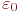 . В этом случае оценка адекватности модели будет более объективна, хотя число наблюдений в эксперименте увеличивается, и экономии их не будет.
. В этом случае оценка адекватности модели будет более объективна, хотя число наблюдений в эксперименте увеличивается, и экономии их не будет.
По уравнению регрессии можно сделать ориентировочную оценку чувствительности отклика к изменению того или иного фактора. Например, в уравнении 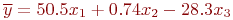 влияние фактора
влияние фактора 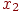 на отклик незначительно по сравнению с другими, так как коэффициент
на отклик незначительно по сравнению с другими, так как коэффициент 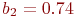 намного меньше остальных коэффициентов.
намного меньше остальных коэффициентов.
В программном пакете MS Excel есть функция "Регрессия", которая может выполнить всесторонний регрессионный анализ данных компьютерного эксперимента.
Пример 5.9. В ремонтное подразделение поступают вышедшие из строя средства связи (СС) с интервалами времени, подчиненными показательному закону с математическим ожиданием 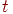 . В каждом СС могут быть неисправными в любом сочетании блоки A, B, C с вероятностями
. В каждом СС могут быть неисправными в любом сочетании блоки A, B, C с вероятностями 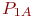 ,
, 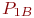 ,
, 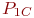 соответственно. Ремонтное подразделение ремонтирует СС путем замены неисправных блоков исправными блоками. В момент поступления неисправного СС в ремонтное подразделение вероятности наличия в нем исправных блоков
соответственно. Ремонтное подразделение ремонтирует СС путем замены неисправных блоков исправными блоками. В момент поступления неисправного СС в ремонтное подразделение вероятности наличия в нем исправных блоков 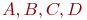 соответственно
соответственно 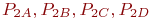 . Наличие и замена блока
. Наличие и замена блока 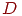 обязательно при любом сочетании неисправных блоков.
обязательно при любом сочетании неисправных блоков.
Построить имитационную модель "Система ремонта" с целью определения вероятности ремонта СС с неисправными блоками  ,
, 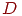 и
и 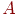 ,
, 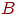 ,
, 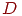 за время
за время 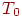 . По результатам эксперимента получить уравнение регрессии, связывающее вероятность ремонта СС с вероятностями
. По результатам эксперимента получить уравнение регрессии, связывающее вероятность ремонта СС с вероятностями 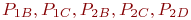 .
.
Решение
Постановка примера 5.9 аналогична постановке примера 3.8. Отличие состоит в том, что введен фактор времени - интервалы поступления неисправных СС. Это учтено в модели, при разработке которой использовался алгоритм примера 3.8 (см. рис. 3.18).
Для построения уравнения регрессии введем обозначения:
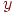 - отклик модели, вероятность ремонта СС с неисправными блоками
- отклик модели, вероятность ремонта СС с неисправными блоками 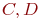 и
и 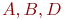 за время
за время 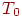 ;
;
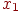 - фактор, представляющий вероятность
- фактор, представляющий вероятность 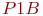 ;
;
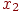 - фактор, представляющий вероятность
- фактор, представляющий вероятность 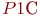 ;
;
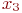 - фактор, представляющий вероятность
- фактор, представляющий вероятность  ;
;
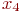 - фактор, представляющий вероятность
- фактор, представляющий вероятность 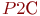 ;
;
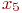 - фактор, представляющий вероятность
- фактор, представляющий вероятность 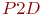 .
.
Исходные данные и результаты эксперимента с моделью в количестве 32 наблюдений приведены в табл. 5.12. По этим данным функция "Регрессия" из MS Excel сформировала искомое уравнение:
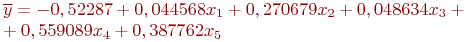
| Таблица 5.12. Результаты эксперимента с моделью "Система ремонта" | ||||||
| № отклика | 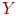
| 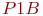
| 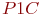
| 
| 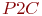
| 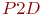
|
| 0,088 | 0,3 | 0,55 | 0,5 | 0,2 | 0,65 | |
| 0,127 | 0,3 | 0,55 | 0,5 | 0,2 | 0,95 | |
| 0,303 | 0,3 | 0,55 | 0,5 | 0,8 | 0,65 | |
| 0,442 | 0,3 | 0,55 | 0,5 | 0,8 | 0,95 | |
| 0,099 | 0,3 | 0,55 | 0,9 | 0,2 | 0,65 | |
| 0,146 | 0,3 | 0,55 | 0,9 | 0,2 | 0,95 | |
| 0,317 | 0,3 | 0,55 | 0,9 | 0,8 | 0,65 | |
| 0,46 | 0,3 | 0,55 | 0,9 | 0,8 | 0,95 | |
| 0,116 | 0,3 | 0,85 | 0,5 | 0,2 | 0,65 | |
| 0,167 | 0,3 | 0,85 | 0,5 | 0,2 | 0,95 | |
| 0,445 | 0,3 | 0,85 | 0,5 | 0,8 | 0,65 | |
| 0,653 | 0,3 | 0,85 | 0,5 | 0,8 | 0,95 | |
| 0,12 | 0,3 | 0,85 | 0,9 | 0,2 | 0,65 | |
| 0,175 | 0,3 | 0,85 | 0,9 | 0,2 | 0,95 | |
| 0,452 | 0,3 | 0,85 | 0,9 | 0,8 | 0,65 | |
| 0,66 | 0,3 | 0,85 | 0,9 | 0,8 | 0,95 | |
| 0,118 | 0,3 | 0,55 | 0,5 | 0,2 | 0,65 | |
| 0,173 | 0,9 | 0,55 | 0,5 | 0,2 | 0,95 | |
| 0,336 | 0,9 | 0,55 | 0,5 | 0,8 | 0,65 | |
| 0,486 | 0,9 | 0,55 | 0,5 | 0,8 | 0,95 | |
| 0,158 | 0,9 | 0,55 | 0,9 | 0,2 | 0,65 | |
| 0,228 | 0,9 | 0,55 | 0,9 | 0,2 | 0,95 | |
| 0,373 | 0,9 | 0,55 | 0,9 | 0,8 | 0,65 | |
| 0,544 | 0,9 | 0,55 | 0,9 | 0,8 | 0,95 | |
| 0,127 | 0,9 | 0,85 | 0,5 | 0,2 | 0,65 | |
| 0,184 | 0,9 | 0,85 | 0,5 | 0,2 | 0,95 | |
| 0,457 | 0,9 | 0,85 | 0,5 | 0,8 | 0,65 | |
| 0,67 | 0,9 | 0,85 | 0,5 | 0,8 | 0,95 | |
| 0,137 | 0,9 | 0,85 | 0,9 | 0,2 | 0,65 | |
| 0,201 | 0,9 | 0,85 | 0,9 | 0,2 | 0,95 | |
| 0,471 | 0,9 | 0,85 | 0,9 | 0,8 | 0,65 | |
| 0,689 | 0,9 | 0,85 | 0,9 | 0,8 | 0,95 |
Кроме вычисленных оценок коэффициентов регрессии функция "Регрессия" выдает также результаты регрессионного анализа (табл. 5.13): вычисленные значения откликов 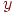 , разность между ними и измеренными в эксперименте в каждом наблюдении
, разность между ними и измеренными в эксперименте в каждом наблюдении  , среднеквадратические ошибки в определении коэффициентов регрессии
, среднеквадратические ошибки в определении коэффициентов регрессии 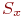 и откликов при определенных значениях факторов
и откликов при определенных значениях факторов 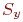 и некоторые другие.
и некоторые другие.
| Таблица 5.13. Результаты регрессионного анализа | |||
| Коэффициенты | Стандартная ошибка | t-статистика | |
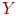 -пересечение -пересечение
| -0,52287 | 0,083821 | -6,23787 |
Переменная 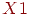
| 0,044568 | 0,034409 | 1,295248 |
Переменная 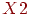
| 0,270679 | 0,068279 | 3,964334 |
Переменная 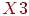
| 0,048634 | 0,051209 | 0,949722 |
Переменная 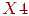
| 0,559089 | 0,034139 | 16,37673 |
Переменная 
| 0,387762 | 0,068279 | 5,679123 |
| Наблюдение | Предсказанное Y | Остатки | Стандартные остатки |
| 0,027558 | 0,060442 | 1,141425 | |
| 0,143886 | -0,01689 | -0,31889 | |
| 0,363011 | -0,06001 | -1,13329 | |
| 0,47934 | -0,03734 | -0,70515 | |
| 0,047011 | 0,051989 | 0,981781 | |
| 0,16334 | -0,01734 | -0,32746 | |
| 0,382465 | -0,06547 | -1,23628 | |
| 0,498794 | -0,03879 | -0,7326 | |
| 0,108761 | 0,007239 | 0,136697 | |
| 0,22509 | -0,05809 | -1,09701 | |
| 0,444215 | 0,000785 | 0,014822 | |
| 0,560544 | 0,092456 | 1,745995 | |
| 0,128215 | -0,00822 | -0,15514 | |
| 0,244544 | -0,06954 | -1,31331 | |
| 0,463669 | -0,01167 | -0,22036 | |
| 0,579998 | 0,080002 | 1,510813 | |
| 0,027558 | 0,090442 | 1,707963 | |
| 0,170627 | 0,002373 | 0,044804 | |
| 0,389752 | -0,05375 | -1,01509 | |
| 0,506081 | -0,02008 | -0,37922 | |
| 0,073752 | 0,084248 | 1,590978 | |
| 0,190081 | 0,037919 | 0,716081 | |
| 0,409206 | -0,03621 | -0,68374 | |
| 0,525535 | 0,018465 | 0,348706 | |
| 0,135502 | -0,00850 | -0,16057 | |
| 0,251831 | -0,06783 | -1,28096 | |
| 0,470956 | -0,01396 | -0,26356 | |
| 0,587285 | 0,082715 | 1,56204 | |
| 0,154956 | -0,01796 | -0,33909 | |
| 0,271285 | -0,07028 | -1,3273 | |
| 0,490410 | -0,01941 | -0,36655 | |
| 0,606739 | 0,082261 | 1,553472 |
Пример 5.10. На узел связи поступают заявки на передачу сообщений. Интервалы времени поступления заявок подчинены показательному закону с математическим ожиданием 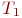 . На узле связи имеются два канала передачи данных. При поступлении очередной заявки в интервале времени
. На узле связи имеются два канала передачи данных. При поступлении очередной заявки в интервале времени  вероятности того, что каналы
вероятности того, что каналы 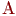 и
и 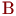 будут свободны, соответственно равны
будут свободны, соответственно равны 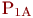 и
и 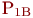 . При поступлении заявок после времени
. При поступлении заявок после времени 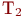 вероятности того, что каналы
вероятности того, что каналы 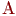 и
и 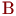 будут свободны, соответственно равны
будут свободны, соответственно равны 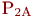 и
и 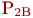 . Сообщение передаётся по любому свободному каналу. Если оба канала заняты, заявка теряется.
. Сообщение передаётся по любому свободному каналу. Если оба канала заняты, заявка теряется.
Построить имитационную модель "Обработка запросов на узле связи" с целью определения абсолютного и относительного числа потерянных заявок из их общего количества, поступивших на узел связи за время 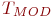 ,
, 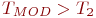 . Получить уравнение регрессии, связывающее относительную долю обслуженных заявок с интервалами их поступления и вероятностями
. Получить уравнение регрессии, связывающее относительную долю обслуженных заявок с интервалами их поступления и вероятностями 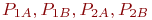 .
.
Решение
Имитационная модель построена в соответствии с алгоритмом (см. рис. 3.21). Для построения уравнения регрессии введем обозначения:
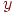 - отклик модели, вероятность ремонта СС с неисправными блоками
- отклик модели, вероятность ремонта СС с неисправными блоками  ,
, 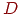 и
и 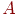 ,
, 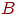 ,
, 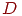 за время
за время 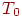 ;
;
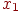 - фактор, представляющий вероятность
- фактор, представляющий вероятность  ;
;
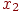 - фактор, представляющий вероятность
- фактор, представляющий вероятность 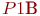 ;
;
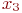 - фактор, представляющий вероятность
- фактор, представляющий вероятность 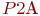 ;
;
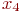 - фактор, представляющий вероятность
- фактор, представляющий вероятность  ;
;
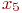 - фактор, представляющий интервалы поступления заявок
- фактор, представляющий интервалы поступления заявок 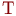 .
.
Исходные данные и результаты эксперимента приведены в табл. 5.14. Для регрессионного анализа также использовалась функция "Регрессия" MS Excel. Получено искомое уравнение:
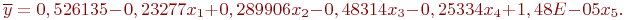
| Таблица 5.14. Результаты эксперимента с моделью "Обработка запросов на узле связи" | ||||||
| Номер отклика | 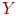
| 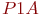
| 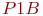
| 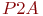
| 
| 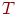
|
| 0,405 | 0,5 | 0,7 | 0,3 | 0,3 | ||
| 0,406 | 0,5 | 0,7 | 0,3 | 0,3 | ||
| 0,09 | 0,5 | 0,7 | 0,3 | 0,9 | ||
| 0,09 | 0,5 | 0,7 | 0,3 | 0,9 | ||
| 0,195 | 0,5 | 0,7 | 0,7 | 0,3 | ||
| 0,195 | 0,5 | 0,7 | 0,7 | 0,3 | ||
| 0,06 | 0,5 | 0,7 | 0,7 | 0,9 | ||
| 0,06 | 0,5 | 0,7 | 0,7 | 0,9 | ||
| 0,38 | 0,5 | 0,9 | 0,3 | 0,3 | ||
| 0,38 | 0,5 | 0,9 | 0,3 | 0,3 | ||
| 0,65 | 0,5 | 0,9 | 0,3 | 0,9 | ||
| 0,65 | 0,5 | 0,9 | 0,3 | 0,9 | ||
| 0,17 | 0,5 | 0,9 | 0,7 | 0,3 | ||
| 0,17 | 0,5 | 0,9 | 0,7 | 0,3 | ||
| 0,035 | 0,5 | 0,9 | 0,7 | 0,9 | ||
| 0,0348 | 0,5 | 0,9 | 0,7 | 0,9 | ||
| 0,375 | 0,9 | 0,7 | 0,3 | 0,3 | ||
| 0,376 | 0,9 | 0,7 | 0,3 | 0,3 | ||
| 0,06 | 0,9 | 0,7 | 0,3 | 0,9 | ||
| 0,06 | 0,9 | 0,7 | 0,3 | 0,9 | ||
| 0,165 | 0,9 | 0,7 | 0,7 | 0,3 | ||
| 0,165 | 0,9 | 0,7 | 0,7 | 0,3 | ||
| 0,03 | 0,9 | 0,7 | 0,7 | 0,9 | ||
| 0,0301 | 0,9 | 0,7 | 0,7 | 0,9 | ||
| 0,37 | 0,9 | 0,9 | 0,3 | 0,3 | ||
| 0,37 | 0,9 | 0,9 | 0,3 | 0,3 | ||
| 0,055 | 0,9 | 0,9 | 0,3 | 0,9 | ||
| 0,055 | 0,9 | 0,9 | 0,3 | 0,9 | ||
| 0,16 | 0,9 | 0,9 | 0,7 | 0,3 | ||
| 0,16 | 0,9 | 0,9 | 0,7 | 0,3 | ||
| 0,025 | 0,9 | 0,9 | 0,7 | 0,9 | ||
| 0,025 | 0,9 | 0,9 | 0,7 | 0,9 |
Результаты регрессионного анализа, аналогичные рассмотренным в примере 5.9 (табл. 5.13), приведены в табл. 5.15.
| Таблица 5.15. Результаты регрессионного анализа | |||
| Коэффициенты | Стандартная ошибка | t-статистика | |
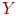 -пересечение -пересечение
| 0,526135 | 0,211881 | 2,483165 |
Переменная 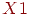
| -0,23277 | 0,112257 | -2,0735 |
Переменная 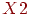
| 0,289906 | 0,224514 | 1,291259 |
Переменная 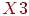
| -0,48314 | 0,112257 | -4,30387 |
Переменная 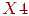
| -0,25334 | 0,074838 | -3,38522 |
Переменная 
| 1,48E-05 | 0,005613 | 0,002645 |
| Наблюдение | Предсказанное Y | Остатки | Стандартные остатки |
| 0,391756 | 0,013244 | 0,113864 | |
| 0,391875 | 0,014125 | 0,12144 | |
| 0,23975 | -0,14975 | -1,28748 | |
| 0,239869 | -0,14987 | -1,2885 | |
| 0,1985 | -0,0035 | -0,03009 | |
| 0,198619 | -0,00362 | -0,03111 | |
| 0,046494 | 0,013506 | 0,116121 | |
| 0,046613 | 0,013387 | 0,1151 | |
| 0,449738 | -0,06974 | -0,59957 | |
| 0,449856 | -0,06986 | -0,60059 | |
| 0,297731 | 0,352269 | 3,02865 | |
| 0,29785 | 0,35215 | 3,027629 | |
| 0,256481 | -0,08648 | -0,74353 | |
| 0,2566 | -0,0866 | -0,74455 | |
| 0,104475 | -0,06948 | -0,59732 | |
| 0,104594 | -0,06979 | -0,60006 | |
| 0,29865 | 0,07635 | 0,656423 | |
| 0,298769 | 0,077231 | 0,664 | |
| 0,146644 | -0,08664 | -0,74492 | |
| 0,146763 | -0,08676 | -0,74595 | |
| 0,105394 | 0,059606 | 0,512468 | |
| 0,105513 | 0,059487 | 0,511447 | |
| -0,04661 | 0,076612 | 0,65868 | |
| -0,04649 | 0,076594 | 0,658519 | |
| 0,356631 | 0,013369 | 0,114939 | |
| 0,35675 | 0,01325 | 0,113918 | |
| 0,204625 | -0,14963 | -1,28641 | |
| 0,204744 | -0,14974 | -1,28743 | |
| 0,163375 | -0,00338 | -0,02902 | |
| 0,163494 | -0,00349 | -0,03004 | |
| 0,011369 | 0,013631 | 0,117195 | |
| 0,011488 | 0,013512 | 0,116174 |
Вопросы для самоконтроля
- Что понимают под характеристикой случайных величин и процессов?
- Что такое несмещенная оценка характеристики случайной величины? Состоятельная? Эффективная?
- Что характеризует гистограмма? Правило построения гистограммы.
- В чем состоит сущность дисперсионного анализа?
- Что такое ошибки первого рода и второго рода при оценке гипотез?
- Что такое F - распределение и почему оно является мерой сравнения дисперсий случайных величин?
- Для чего используется критерий Вилькоксона?
- В чем состоит методика выявления несущественных факторов?
- Назначение корреляционного анализа.
- Назначение регрессионного анализа.
- Представьте графически виды корреляции между двумя переменными.
- Составьте систему уравнений для определения коэффициентов регрессии модели вида:
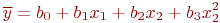
- Для линейной и нелинейной моделей, полученных в п. 5.12, вычислить и сравнить ошибки
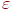 и
и 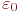 .
. - С объектом проведено
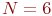 экспериментов. Данные экспериментов приведены в таблице:
экспериментов. Данные экспериментов приведены в таблице:
| Измерения | Эксперименты | 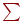
| |||||
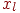
| |||||||

| |||||||
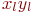
| |||||||
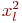
| |||||||
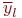
| |||||||

|
- Построить линейную математическую модель функционирования объекта вида:
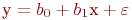 . Расчеты провести в таблице. Проверьте адекватность модели при абсолютной точности 0,2.
. Расчеты провести в таблице. Проверьте адекватность модели при абсолютной точности 0,2.

