Контактная разность потенциалов. Если два различных металла привести в соприкосновение, то между ними возникает разность потенциалов

Если два различных металла привести в соприкосновение, то между ними возникает разность потенциалов, называемая контактной разностью потенциалов. Итальянский физик А. Вольта (1745—1827) установил, что если металлы А1, Zn, Sn, Pb, Sb, Bi, Hg, Fe, Cu, Ag, Au, Pt, Pd привести в контакт в указанной последовательности, то каждый предыдущий при соприкосновении с одним из следующих зарядится положительно. Этот ряд называется рядом Вольта. Контактная разность потенциалов для различных металлов составляет от десятых до целых вольт.

Вольта экспериментально установил два закона:

1. Контактная разность потенциалов зависит лишь от химического состава и температуры соприкасающихся металлов.

2. Контактная разность потенциалов последовательно соединенных различных проводников, находящихся при одинаковой температуре, не зависит от химического состава промежуточных проводников и равна контактной разности потенциалов, возникающей при непосредственном соединении крайних проводников.

Для объяснения возникновения контактной разности потенциалов воспользуемся представлениями зонной теории. Рассмотрим контакт двух металлов с различными работами выхода А1 и А2, т.е. с различными положениями уровня Ферми (верхнего заполненного электронами энергетического уровня). Если A1<A2 (этот случай изображен на рис. 1, а), то уровень Ферми располагается в металле 1 выше, чем в металле 2. Следовательно, при контакте металлов электроны с более высоких уровней металла 1 будут переходить на более низкие уровни металла 2, что приведет к тому, что металл 1 зарядится положительно, а металл 2 — отрицательно. Одновременно происходит относительное смещение энергетических уровней: в металле, заряжающемся положительно, все уровни смещаются вниз, а в металле, заряжающемся отрицательно, — вверх. Этот процесс будет происходить до тех пор, пока между соприкасающимися металлами не установится равновесие, которое, как доказывается в статистической физике, характеризуется совпадением уровней Ферми в обоих металлах (рис. 1, б).

Так как для соприкасающихся металлов уровни Ферми совпадают, а работы выхода А1 и A2 не изменяются (они являются константами металлов и не зависят от того, находятся металлы в контакте или нет), то потенциальная энергия электронов в точках, лежащих вне металлов в непосредственной близости к их по­верхности (точки А и В на рис. 1, б), будет различной. Следовательно, между точками А и В устанавливается разность потенциалов, которая, как следует из рисунка, равна

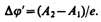(1.1)

Разность потенциалов, обусловленная различием работ выхода контактирующих металлов, называется внешней контактной разностью потенциалов. Чаще говорят просто о контактной разности потенциалов, подразумевая под ней внешнюю.

Если уровни Ферми для двух контактирующих металлов не одинаковы, то между внутренними точками металлов наблюдается внутренняя контактная разность потенциалов, которая, как следует из рисунка, равна

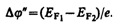(1.2)

В квантовой теории доказывается, что причиной возникновения внутренней контактной разности потенциалов является различие концентраций электронов в контактирующих металлах

Если, например, привести в соприкосновение три разнородных проводника, имеющих одинаковую температуру, то разность потенциалов между концами разомкнутой цепи равна алгебраической сумме скачков потенциала во всех контактах. Онане зависит от природы промежуточных проводников (второй закон Вольта).

Внутренняя контактная разность потенциалов возникает в двойном электрическом слое, образующемся в приконтактной области и называемом контактным слоем. Толщина контактного слоя в металлах составляет примерно 10^-10 м, т. е. соизмерима с междоузельными расстояниями в решетке металла. Число электронов, участвующих в диффузии через контактный спой, составляет примерно 2% от общего числа электронов, находящихся на поверхности металла. Столь незначительное изменение концентрации электронов в контактном слое, с одной стороны, и малая по сравнению с длиной свободного пробега электрона его толщина — с другой,

не могут привести к заметному изменению проводимости контактного слоя по сравнению с остальной частью металла. Следовательно, электрический ток через контакт двух металлов проходит так же легко, как и через сами металлы, т.е. контактный слой проводит электрический ток в обоих направленияходинаково и не дает эффекта выпрямления, который всегда связан с односторонней проводимостью.

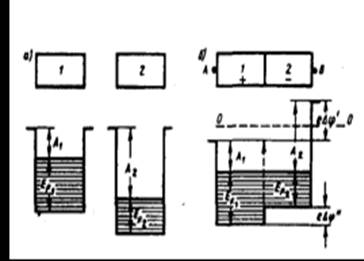рис. 1

3. Термоэлектрические явления

Термоэлектрические явления объединяют группу физических процессов, обусловленных взаимными превращениями энергии теплового движения и энергии электрического тока. К ним относят обычно три эффекта - Зеебека, Пельтье и Томсона.

Эффект Зеебека (1821 г.) заключается в том, что в электрической цепи, состоящей из последовательно соединенных элементов, изготовленных из различных материалов, возникает электрический ток, если места контактов поддерживаются при неодинаковых температурах. При разрыве одного из проводников на концах цепи возникает разность потенциалов - термоэлектродвижущая сила (термоЭДС, ТЭДС). Электрическая цепь, в которой возникает термоЭДС, называется термоэлектрической цепью, а материалы, из которых составлена термоэлектрическая цепь, - термоэлектродами. Пара разнородныхтермоэлектродов, гальванически соединенных на одном конце (в виде рабочего спая), образуют термопару - чувствительный элемент термоэлектрического преобразователя. Обычно в метрологической практике оценку термоЭДС конкретного материала проводят по отношению к термоэлектроду из чистой платины (нормальному платиновому термоэлектроду).

Сегодняшних знаний о причинах и механизме возникновения термоЭДС недостаточно для ее точного вычисления. Отсутствие общепризнанной теории возникновения термоЭДС обусловлено чрезвычайной сложностью механизмов процесса. ТермоЭДС реального металла зависит от распределения электронов по скоростям (энергиям), связанного с температурой и энергией Ферми, строения решетки металла, интенсивности ее колебаний, механизмов рассеяния носителей тока на реальной решетке, примесных атомах, фононах и между собой. Сложность связей приводит к тому, что коэффициенты термоЭДС различных металлов и сплавов значительно отличаются друг от друга и от теоретически предсказанных значений.

Эффект Пельтье (1834 г.) состоит в том, что при прохождении тока в цепи с проводниками из разнородных материалов в местах контактов помимо выделения джоулевой теплоты поглощается или выделяется (в зависимости от направления тока и типа вещества) некоторое количество теплоты:

Qр=ПּIּτ,

где П - коэффициент Пельтье; I - сила тока; τ - время.

Эффект Пельтье проявляется именно в спаетармопары, что позволяет использовать его для таких практических задач, как контроль качества рабочего спая и диагностика качества заделки рабочего спая натермометрируемом объекте.

Эффект Томсона (1856 г.) заключается в том, что в зависимости от направления тока при его прохождении по однородному проводнику, вдоль которого имеется градиент температуры (т.е. при наличии в цепи одновременно и электрического тока, и потока теплоты), в объеме однородного проводника выделяется или поглощается теплота. Эта теплота выделяется (поглощается) в дополнение к выделяющейся теплоте Джоуля - Ленца (резистивный нагрев).

Количество теплоты Томсона Qσ пропорционально силе тока I и градиенту температуры ∆T:

Qσ = σּIּ∆Tּτ,

где σ – коэффициент Томсона, В/К-1, τ - время, с.

В замкнутой цепи, по которой протекает ток, при наличии градиента

температуры возникают все три термоэлектрических явления, связанных между собой соотношениями Кельвина, позволяющими определять величину любого из трех эффектов, если известна величина хотя бы одного из них.

На эффекте Зеебека основано измерение температуры с помощью термоэлектрических преобразователей (термопар): величина термоЭДС оказывается пропорциональной разности функций температур спаев термоэлектрической цепи. При незначительных разностях температур спаев можно принять, что развиваемая термоЭДС пропорциональна ∆Т. То есть, если точки спаев двух проводников термоэлектрической цепи помещены в среды с разными температурами (рис.2), то

∆Е=аּ∆Т, (2.1)

или в дифференциальной форме

dE = aּdT, (2.2)

где ∆Е - термоЭДС, a -дифференциальная или удельная термоЭДС данной пары металлов. Измеряется она в В/К и существенно зависит от природы контактирующих материалов, а также интервала температур, достигая порядка 10^-5 ÷10^-4 В/К. В небольшом интервале температур (0-100°С) удельная термоЭДСслабо зависит от температуры

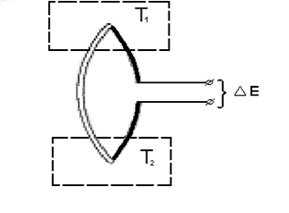рис. 2Схема термоэлектрической цепи.

Из (2.1) следует, что a численно равен величине термоЭДС, возникающей в цепи при разности температур спаев, равной одному градусу. Термоэлектрический коэффициент а обычно измеряется в вольтах (милливольтах) на градус. В общем случае величина a является функцией температуры.

Если принять для упрощения, что a ≠f(T), то, интегрируя уравнение (2.2), получим

Е2-Е1= aּ(Т2-Т1), (2.3)

где индексы 1 и 2 относятся соответственно к горячему и холодному спаям термоэлектрической цепи (условимся называть горячим тот спай цепи, который находится при более высокой температуре; другой спай будем именовать холодным, т.е. Т2>Т1).

Понятно, что если замкнуть эту цепь через какое-либо внешнее электрическое сопротивление (обмотка электродвигателя, электронагреватель и т. д.), то в термоэлектрической цепи возникает ток (рис. 3).

Если изменить температуры спаев на обратные (т. е. спай, находя-щийся при

температуре Т1, поместить в среду с температурой Т2, а другой спай, температура которого была равна Т2, поместить в среду с температурой Т1), то в цепи возникает ток, равный по величине току при прежних температурах спаев, но текущий в противоположном направлении.

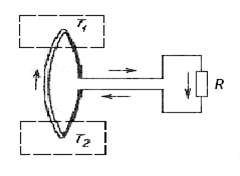Рис. 3. Схема термоэлектрического генератора.

Из изложенного следует, что термоэлектрический эффект, в принципе, может быть использован для целей производства электроэнергии. Впервые вопрос о создании термоэлектрического генератора, основанного на использовании эффекта Зеебека, был поставлен еще в 1885 г. английским физиком Рэлеем. Однако долгое время эта идея не была реализована вследствие того, что известные в то время термоэлектродные материалы позволяли соорудить термоэлектрические генераторы лишь с очень малыми значениями термоэлектрического КПД. И хотя впоследствии были созданы перспективные полупроводниковые термоэлектрические генераторы, значительно более широкое использование получил эффект Зеебека в измерительной технике при измерении температур термоэлектрическими преобразователями.

Измерив величину термоЭДС Е1-Е2 и зная температуру одного из спаев термопары, можно определить температуру среды, в которую помещен другой (рабочий) спай. Разумеется, для этого надо знать значение коэффициента a, которое определяется предварительной тарировкой (градуировкой).

В современной термометрии термоэлектрические термометры занимают наибольший удельный вес, составляя около 55 % от общего числа контактных термометров, применяющихся на промышленных предприятиях и в научных учреждениях.

термоЭДС термопары обусловлена тремя причинами. Первая заключается в зависимости уровня Ферми энергии электронов в проводнике от

температуры, что приводит к неодинаковым скачкам потенциала при переходе из одного металла в другой в спаях термопары, находящихся при разных температурах. Во-вторых, при наличии градиента температуры электроны в области горячего конца проводника приобретают более высокие энергии и подвижность. Вдоль проводника возникает градиент концентрации электронов с повышенными значениями энергии, что влечет за собой диффузию более быстрых электронов к холодному концу, а более медленных - к горячему. Но диффузионный поток более быстрых электронов оказывается больше. В-третьих, при наличии градиента температуры вдоль проводника возникает дрейф фононов - квантов энергии колебаний кристаллической решетки. Сталкиваясь с электронами, фононы сообщают им направленное движение от более нагретого конца проводника к более холодному. Последние два процесса приводят к избытку электронов вблизи холодного конца и недостатку их вблизи горячего конца. В результате внутри проводника возникает электрическое поле, направленное навстречу градиенту температуры. Таким образом, термоЭДС термопары возникает только из-за наличия продольного градиента температуры в проводниках, составляющих термопару.

Термоэлектродвижущая сила, развивающаяся на концах однородного проводника (ТЭДС Томсона), зависит от его природы, а ее величина для конкретного проводника А определяется соотношением

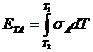(2.4)

где σА- коэффициент Томсона для проводника А; Т2>Т1.

Если из одного однородного проводника А составить замкнутую цепь (рис.4 а) и поддерживать в ее крайних точках температуры Т1 и Т2, то вследствие кругового движения за-рядов по замкнутой цепи направление движения их в одной половине цепи будет совпадать с положительным направлением градиента температуры, а в другой - с отрицательным. Поэтому в обеих ветвях цепи возникают ТЭДС Томсона, равные по величине и противоположные по знаку, которые во всей замкнутой цепи взаимно компенсируются. Таким образом, в замкнутой цепи, состоящей из одного однородного проводника, ТЭДС Томсона равна нулю при любом

распределении температуры вдоль проводника. Если же замкнутая цепь состоит из двух различных однородных проводников А и В (рис. 4 б), то суммарная ТЭДС Томсона в цепи

равна разности ТЭДС, возникающих в каждой ветви, и определяется по

формуле

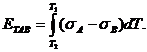(2.5)

То есть в замкнутой цепи, состоящей из пары проводников А и В, суммарная ТЭДС зависит от температур Т1 и Т2 в местах их соединения

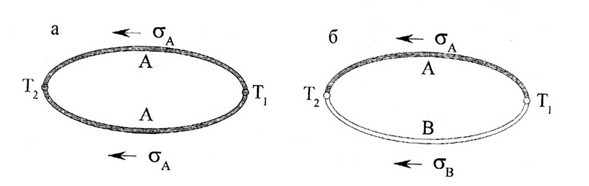
Рис. 4. Распределение потенциалов в цепи идеальной (с однородными по всей длине термоэлектродами) термопары: а - замкнутая цепь из одного однородного проводника А; б - замкнутая цепь из пары однородных проводников А и В.

Date: 2015-07-17; view: 1631; Нарушение авторских прав