
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Глава 2. Статистические методы моделирования и прогнозирования связей
|
|
2.1. Статистические методы выявления наличия корреляционной связи
Метод взаимозависимых параллельных рядов. Суть метода взаимозависимых параллельных рядов заключается в установлении связей между экономическими явлениями и процессами посредством сопоставления двух или нескольких рядов показателей.
Показатели, касающиеся факторного (детерминирующего) признака, располагаются по возрастанию либо убыванию в зависимости от эволюции исследуемого явления или процесса. Операция продолжается путем параллельной записи значений результативных (детерминируемых) признаков. Затем, сравнивая расположенные таким образом ряды значений, выявляют существование связи и ее направление. (Отметим, что возможность связи обоснована предварительным анализом.) Можно сравнивать временные (динамические) и территориальные ряды, ряды распределения.
При сравнении временных рядов нужен предварительный экономический анализ, подтверждающий существование связи между исследуемыми явлениями или процессами, данные должны относиться к достаточно продолжительному периоду времени, чтобы можно было отчетливо выделить тенденцию связи между явлениями.
При исследовании существования связи между экономическими явлениями или процессами, выраженными динамическими рядами, необходимо помнить, что аргумент 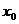 функции является фактором-причиной, а не фактором-временем.
функции является фактором-причиной, а не фактором-временем.
Примером связи между показателями двух динамических рядов служит зависимость между основными производственными фондами на одного рабочего и производительностью труда. Между этими явлениями существует тесная связь.
Преимущество рассмотренного метода – простота его использования. Основной недостаток состоит в субъективной оценке существования зависимости.
Рассмотрим приведенные в табл. 2.1 данные, характеризующие связь между личным доходом X (день. ед.) и личными сбережениями Y (день. ед.).
Т а б л и ц а 2.1
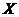
| 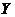
| 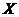
| 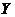
| 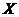
| 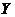
| ||
| 11,2 8,8 13,3 | 18,9 19,6 21,2 | 20,4 22,9 23,0 |
Из простого сопоставления этих рядов можно легко установить, что возрастание значения факторного признака X – личного дохода (187; 190; 200; 216; 240; 251; 251; 262; 267) определяет возрастание результативного признака Y – личных сбережений (8,8; 11,2; 13,3; 18,9; 19,6; 21,2; 20,4; 22,9; 23,0). В данном случае между факторным и результативным признаками существует прямая связь.
Метод статистических группировок. Установление связи между двумя или несколькими экономическими явлениями начинается с группировки данных по факторному признаку. Затем вычисляют средние значения для результативного признака по группам, на которые была разбита статистическая совокупность. Вычисленные средние значения результативного признака позволяют устанавливать связь между изучаемыми признаками, показывая среднее влияние определенного фактора в рамках каждой группы.
Отметим, что объективность связи и влияния каждого факторного признака на изменения результативного признака зависят от количества исходных данных и однородности данных в группах. Чем большим числом исходных данных мы располагаем и чем однороднее данные в группах, тем объективнее информация о связи и влиянии факторного признака на результативный.
Кроме того, при исследовании зависимости между экономическими явлениями следует знать, являются ли изучаемые признаки количественными или качественными (атрибутивными).
В экономике выделяют три варианта комбинаций двух признаков:
1) оба признака количественные (например, стаж работы и средняя почасовая оплата; заработная плата и производительность труда и т.д.);
2) один признак количественный, а другой качественный (например, профессия и заработная плата; порода коров и производство молока; вид почвы и средний урожаи с гектара и т.д.);
3) оба признака качественные (например, профессия и образование; социальное происхождение и социальное положение и т.д.).
При изучении связи между количественными признаками выбирают основной факторный признак, разбивают его на группы, затем вычисляют средние значения результативного признака. После составления таблиц приступают к сравнению вычисленных данных, переходя от одной группы к другой. Прослеживая изменения групповых средних, устанавливают связь между изучаемыми признаками.
Величину интервала группировки и, следовательно, число групп можно установить из формулы Стерджеса (1.1).
Интервалы могут быть равными и неравными, если факторные признаки имеют большую и разнообразную вариацию, хотя объем исследуемой совокупности небольшой.
Изучая зависимость между количественными и качественными признаками, за признак группировки можно принимать любой из них. Если группы составляют по качественному признаку, например по виду почвы (тяжелая, средняя, легкая), то вычисляют средние значения результативного признака и проводят анализ существования связи на основании таблицы. Если же в основу группировки положен количественный признак, то для результативного признака, который является качественным, нельзя вычислить групповые средние, так как атрибутивные признаки не имеют числового выражения. Поэтому для каждой из групп вычисляют относительные величины, выражающие удельный вес единиц, характеризуемых качественным признаком в пределах исследуемой совокупности.
Изучение существования связи между двумя качественными признаками проводится следующим образом: строится группировка по факторному признаку, затем вычисляются показатели удельного веса для каждой группы результативного признака и проводится сравнение полученных результатов.
Для характеристики сложных взаимных связей между тремя, четырьмя и более явлениями применяется комбинированная группировка. При этом статистическая совокупность сначала разбивается на группы по одному признаку, затем каждая из полученных групп разбивается на более мелкие группы по другому признаку и т.д. Во избежание слишком большей раздробленности рекомендуют выбрать два или три группировочных признака, составив для каждого из них группы сравнимы и закрытыми интервалами. Закончив группировку, вычисляют средние или относительные значения результативного признака для созданных групп и подгрупп. Вычисленные показатели сравниваются и анализируются в тесной связи с изменением признаков, положенных в основу группировки.
Простые и комбинированные статистические группировки, применяемые для установления связи между экономическими явлениями, могут быть наглядно представлены в виде группировочных и комбинационных таблиц.
Рассмотрим сначала связь между двумя количественными признаками: личным доходом и личными сбережениями (см. табл. 2.1). Разобьем факторный признак X – личный доход – на группы. Интервал группировки определим по формуле (1.1). Получим h = 19,18. Составим табл. 2.2, в которой указаны интервалы (группы) факторного признака и средние величины соответствующих значений результативного признака. Так, например, 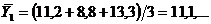
Т а б л и ц а 2.2
| Интервал факторного признака X | Среднее значение результативного признака Y |
| 189,00 – 206,18 206,18 – 225,36 225,36 – 244,54 244,54 – 263,72 263,72 – 282,90 | 11,1 18,9 19,6 21,5 23,0 |
Переходя от одного интервала к другому и прослеживая изменение групповых средних результативного признака, можно констатировать, что между личным доходом и личными сбережениями существует довольно сильная зависимость. Возрастанию величины интервала личных доходов непременно соответствует возрастание личных сбережений.
Исследуем связь между качественным и количественным признаками. В табл. 2.3 составлены группы по качественному признаку – образованию рабочих (неполное среднее, среднее, профессионально-техническое) и вычислена средняя заработная плата соответствующих групп рабочих.
Т а б л и ц а 2.3
| Образование | Неполное среднее Среднее Профессионально-техническое |
| Средняя заработная плата, ден. ед. | 2,075 2,2 2,5 |
Анализ табл. 2.3 показывает, что существует связь между качественным и количественным признаками.
Рассмотрим пример исследования связи между качественным и количественным признаками, когда в основу группировки положен количественный признак. В табл. 2.4 приведена группировка 400 кооперативов одной из областей Республики Беларусь по основным фондам (факторный признак). Результативный признак – передовые, средние и слабые кооперативы – является атрибутивным. Для него нельзя вычислять групповые средние, так как атрибутивные признаки не имеют численного значения. В этом случае вычисляются относительные величины, выражающие удельный вес единиц, характеризуемых качественным признаком в пределах исследуемой совокупности.
Т а б л и ц а 2.4
| Интервал основных фондов | Кооперативы | Всего по области | ||
| передовые | средние | слабые | ||
| до 20 20-30 30-40 40-50 50-60 60-70 70-80 80-90 90-100 100-110 110-120 120-130 130-140 140-150 Свыше 150 | - - - - - - 1,6 3,4 5,0 7,9 7,0 21,2 37,5 10,3 6,1 | - - - - - 6,4 7,1 18,3 37,4 25,0 3,8 2,0 - - - | 10,1 29,9 41,2 9,0 4,3 2,5 1,0 2,0 - - - - - - - | 1,8 3,7 5,2 6,0 6,8 8,0 9,5 18,8 15,2 8,3 7,0 3,0 2,5 2,2 2,0 |
| В с е г о, % |
Исследуя связь между величиной основных фондов и последовательным расположением кооперативов по признакам их развития и укрепления, отмечаем, что слаборазвитые кооперативы входят в своей совокупности в интервалы до 100 ден. ед.; передовые кооперативы в большинстве случаев (90%) сгруппированы в высшие интервалы – с основными фондами свыше 100 ден. ед., а средние кооперативы входят в центральные интервалы от 60 до 130 ден. ед..
Рассмотрим пример связи между двумя атрибутивными признаками: видом обучения рабочих (курсы на производстве и профессионально-технические училища) – факторный признак – и удельным весом рабочих, дававших брак при выполнении фиксированной сложной операции обработки деталей – результативный признак. Результаты статистических наблюдений представлены в табл. 2.5.
Т а б л и ц а 2.5
| Y X | Профессионально-технические училища | Курсы на производстве | |||
| число рабочих | % | число рабочих | % | ||
| Удельный вес рабочих, дававших брак, % | 211 81,2 | 96 61,9 | |||
| Всего рабочих | |||||
Из таблицы четко прослеживается связь между исследуемыми атрибутивными признаками. Кроме того, анализ взаимосвязи признаков позволяет сделать вывод о том, что способ получения квалификации является одним из главных факторов выпуска качественной продукции.
Для характеристики сложных взаимосвязей применяются комбинированные группировки.
Так как объем учебника ограничен, а подробное изложение этого метода требует много места, то отошлем читателей к книге [16].
Корреляционная таблица. Специальной формой комбинационной таблицы является корреляционная таблица. Она охватывает два зависимых ряда распределения, один из которых представляет факторный признак (X), другой – результативный (Y).
Если в корреляционной таблице частоты группируются около диагонали, соединяющей левый верхний (нижний) и правый нижний (верхний) углы таблицы, то между исследуемыми явлениями существует прямая (обратная) связь, т.е. возрастание или уменьшение факторного признака влечет за собой возрастание (уменьшение) или уменьшение (возрастание) результативного признака. Такая концентрация частот отражает прямую вариацию исследуемых признаков. При этом интенсивная концентрация частот около диагонали указывает на существование тесной связи между явлениями, а рассеивание частот по всей таблице свидетельствует об отсутствии связи.
Рассмотрим связь между личным доходом и личными сбережениями (см. табл. 2.1). Построим корреляционную таблицу, разбив предварительно факторный и результативные признаки на интервалы длиной 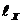 =19,18 и
=19,18 и 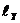 =2,83 и подсчитав число значений признаков, входящих в данные интервалы. Корреляционная таблица будет иметь вид табл. 2.6.
=2,83 и подсчитав число значений признаков, входящих в данные интервалы. Корреляционная таблица будет иметь вид табл. 2.6.
Т а б л и ц а 2.6
| Личные сбережения Y | Личный доход X | Личный доход X | |||||
| 187,0-206,18 | 206,18-225,36 | 225,36-244,54 | 244,54-263,72 | 263,72-282,90 | |||
| 8,80–1,63 11,63–14,46 14,46–17,29 17,29–20,12 20,12–23,00 | - - - | - - - - | - - - - | - - - - | - - - - | - | |
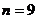
| |||||||
Концентрация частот около диагонали, соединяющей левый верхний угол с правым нижним углом, указывает на тесную прямую связь между личным доходом и личными сбережениями.
Графический метод. Графический метод исследования связи состоит в следующем: строится прямоугольная система координат; значения факторного признака 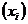 откладываются на оси абсцисс, а на оси ординат откладываются значения результативного признака
откладываются на оси абсцисс, а на оси ординат откладываются значения результативного признака 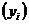 . Результат каждого наблюдения отображается точками
. Результат каждого наблюдения отображается точками 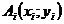 . Расположение точек на графике отражает существование или отсутствие связи между факторным и результативным признаками.
. Расположение точек на графике отражает существование или отсутствие связи между факторным и результативным признаками.
Изображение на плоскости всех парных значений двух переменных X и У называется диаграммой рассеяния или корреляционным полем.
Тесная группировка точек около одной определенной линии, выражающей форму связи (прямолинейной, параболической, гиперболической и т.д.), указывает на сильную связь между факторным и результативным признаками. Рассеянное расположение точек на графике доказывает отсутствие связи между признаками.
Таким образом, диаграмма рассеяния позволяет более наглядно выделять меру совместного изменения (ковариации) двух переменных, т.е. с помощью корреляционного поля можно уловить форму и тенденцию зависимости между факторным и результативным признаками.
Рассмотрим изучение зависимости личных сбережений (Y) от личного дохода (X).
На рис. 2.1 представлена диаграмма рассеяния, соответствующая результатам, приведенным в табл. 2.1. Координатами точек диаграммы являются величины личного дохода и личных сбережений. По скоплению точек на диаграмме видно, что с увеличением личного дохода наблюдается ясно выраженная тенденция роста личных сбережений. Эта тенденция имеет явно линейный характер, благодаря чему можно попытаться аппроксимировать рассматриваемую зависимость линейной функцией регрессии. Конечно, эта тенденция существует лишь в среднем, так как она нарушается отклонениями отдельных точек. Отклонения от прямой объясняются влиянием прочих неучтенных или случайных факторов.
Рассмотренные методы исследования зависимости сравнительно просты, но их значение неоспоримо, поскольку они дают полезную информацию о сущности и характере исследуемой связи. Результаты, полученные элементарными методами, служат основой для применения более сложных методов анализа.
Вопросы для самопроверки
1. Назовите методы исследования зависимости между экономическими явлениями.
2. Изложите суть метода взаимозависимых параллельных рядов.
3. Какие варианты комбинации признаков встречаются в экономике?
4. Охарактеризуйте метод исследования сложных взаимных связей между тремя, четырьмя и более явлениями.
5. Как строится корреляционная таблица?
6. Какой метод применяется для визуальной оценки зависимости между экономическими явлениями?
Задача. По данным, приведенным в табл. 2.7, выявите, применив методы исследования зависимости, существует ли связь между валовой продукцией на одного среднегодового работника сельского хозяйства (Y, день. ед.) и нагрузкой сельскохозяйственных угодий на одного работника (X, га/чел.).
Т а б л и ц а 2.7
| X | Y | X | Y | X | Y | ||
| 10,521 7,804 7,616 6,810 8,235 5,744 7,376 8,761 6,594 9,763 | 8,113 7,677 8,685 11,551 9,185 5,880 8,583 10,019 8,764 8,806 | 9,091 7,318 8,479 9,699 9,653 8,803 10,563 9,251 11,294 12,506 |
2.2. Методы проверки существенности статистических связей
Критерий 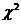 проверки существенности связи. Пусть для установления связей между экономическими явлениями составлена группировочная (корреляционная) таблица. Проверим объективность связи с помощью критерия
проверки существенности связи. Пусть для установления связей между экономическими явлениями составлена группировочная (корреляционная) таблица. Проверим объективность связи с помощью критерия 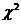 . Для этого выдвинем гипотезу, что между двумя признаками нет никакой связи, а наблюдаемая связь обусловлена случайными вариациями. На основании этой гипотезы перестраиваем корреляционную таблицу: частоты в месте пересечения i -й строки с j -м столбцом заменяем теоретическими частотами
. Для этого выдвинем гипотезу, что между двумя признаками нет никакой связи, а наблюдаемая связь обусловлена случайными вариациями. На основании этой гипотезы перестраиваем корреляционную таблицу: частоты в месте пересечения i -й строки с j -м столбцом заменяем теоретическими частотами 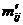 , вычисленными по формуле
, вычисленными по формуле
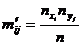 , (2.1)
, (2.1)
где 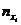 – сумма частот i -й строки;
– сумма частот i -й строки; 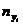 – сумма частот j -столбца; n – объем выборки.
– сумма частот j -столбца; n – объем выборки.
Затем находим величину
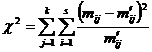 , (2.2)
, (2.2)
которая подчиняется распределению 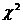 c
c 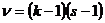 степенями свободы.
степенями свободы.
Задавая уровень значимости 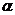 = 0,05, находим по таблице
= 0,05, находим по таблице 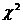 -распределения критическое значение
-распределения критическое значение 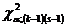 . Если вычисленное значение
. Если вычисленное значение 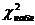 превышает табличное
превышает табличное 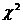 , то гипотеза независимости переменных отвергается с вероятностью 0,95 и, следовательно, с вероятностью 0,95 можно утверждать, что между обеими переменными существует связь.
, то гипотеза независимости переменных отвергается с вероятностью 0,95 и, следовательно, с вероятностью 0,95 можно утверждать, что между обеими переменными существует связь.
Для объективной оценки связи между экономическими явлениями при использовании критерия 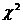 наблюдения должны быть независимы, выборка – случайной, объем выборки – достаточно большим, данные должны быть выражены в абсолютных единицах, а не в процентах.
наблюдения должны быть независимы, выборка – случайной, объем выборки – достаточно большим, данные должны быть выражены в абсолютных единицах, а не в процентах.
Пример 2.1. По данным, приведенным в табл. 2.8, установить и с помощью критерия 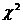 проверить существенность статистической связи между средним текущим доходом (X, день. ед.) и средним расходом (Y, день. ед.) семьи.
проверить существенность статистической связи между средним текущим доходом (X, день. ед.) и средним расходом (Y, день. ед.) семьи.
Т а б л и ц а 2.8
| X | Y | X | Y | X | Y | ||
| 4,60 6,11 4,79 4,05 6,04 4,17 4,57 5,01 3,95 | 4,40 5,54 4,91 4,10 5,59 4,25 5,48 4,56 3,84 | 6,35 4,49 6,04 4,51 4,58 4,59 4,55 5,07 4,18 | 6,06 4,40 4,70 4,69 4,54 4,28 4,78 5,10 4,19 | 4,02 4,78 4,82 4,45 4,88 5,71 5,58 4,60 | 4,26 4,78 4,73 4,33 4,72 5,26 5,04 4,40 |
Для анализа зависимости между средним доходом и средним расходом семьи построим диаграмму рассеяния (рис. 2.2).
Скопление точек на диаграмме указывает на то, что с ростом текущих доходов возрастают и средние расходы семьи. Эта тенденция имеет явно линейный характер.
Строим корреляционную таблицу (табл. 2.9), определив предварительно длины интервалов признаков по формуле (1.1). Тогда 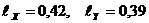 .
.
Т а б л и ц а 2.9
| Y | X | 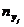
| |||||
| 3,95-4,37 | 4,37-4,79 | 4,79-5,21 | 5,21-5,63 | 5,63-6,06 | 6,06-6,48 | ||
| 3,84 – 4,23 4,23 – 4,62 4,62 – 5,00 5,00 – 5,40 5,40 – 5,79 5,79 – 6,18 | - - - - | - - - | - - - - | - - - - - | - - - | - - - - | |
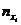
| n=26 |
Перестроим корреляционную таблицу, заменив частоты 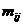 в месте пересечения i -й строки и j -го столбца теоретическими частотами
в месте пересечения i -й строки и j -го столбца теоретическими частотами 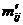 вычисленными по формуле (2.1). Тогда
вычисленными по формуле (2.1). Тогда
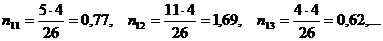
Полученные результаты запишем в виде следующей матрицы:

Затем по формуле (2.2) вычислим критерий
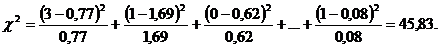
Для нашего примера число степеней свободы  = (6-1)(6-1) = 25. По таблице распределения
= (6-1)(6-1) = 25. По таблице распределения 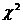 при уровне значимости
при уровне значимости 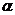 = 0,05 находим критическое значение
= 0,05 находим критическое значение 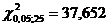 . Так как
. Так как 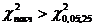 , то между средним доходом и средним расходом семьи существует значимая статистическая связь.
, то между средним доходом и средним расходом семьи существует значимая статистическая связь.
Дисперсионный анализ проверки объективности связи. Суть дисперсионного анализа заключается в расчленении общей вариации данных на части и в сравнении полученных частных дисперсий. При этом предполагается, что если наблюденные данные представляют случайную выборку из нормально распределенной генеральной совокупности, то значения всех дисперсий должны оказаться приблизительно пропорциональными степеням свободы, с которыми они вычисляются, и каждую из них можно рассматривать как приближенное выражение генеральной дисперсии. Следовательно, допускается, что расхождение между ними может быть лишь случайным. Поэтому расхождение значений дисперсии, выходящих за известные пределы при данном числе степеней свободы и принятой доверительной вероятности, свидетельствует об отсутствии связей.
Предположим, что изучается влияние фактора на признак X (наблюдаемую случайную величину), при этом проведено k (k >2) серий наблюдений. Серии наблюдений рассматриваем как k (k >2) независимых нормально распределенных случайных величин 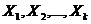 с одинаковыми дисперсиями
с одинаковыми дисперсиями 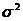 , тогда как математические ожидания (центры распределения)
, тогда как математические ожидания (центры распределения) 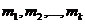 могут быть различны. Пусть над каждой из случайных величин
могут быть различны. Пусть над каждой из случайных величин 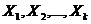 проводится
проводится 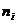 независимых наблюдений:
независимых наблюдений:

Необходимо, опираясь на статистические данные, проверить гипотезу 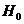 о том, что математические ожидания всех случайных величин
о том, что математические ожидания всех случайных величин 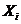 ,
, 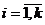 одинаковы, т.е.
одинаковы, т.е. 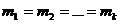 . Если гипотеза
. Если гипотеза 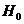 верна, то статистические средние каждой серии не должны значительно отличаться друг от друга. Если же статистические средние серий значительно различаются, то гипотеза
верна, то статистические средние каждой серии не должны значительно отличаться друг от друга. Если же статистические средние серий значительно различаются, то гипотеза 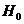 должна быть отвергнута.
должна быть отвергнута.
В простейшем случае дисперсионного анализа общая сумма квадратов отклонений представляется в виде суммы квадратов отклонений групповых средних от общей средней и суммы квадратов отклонений внутри групп:
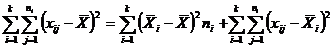 ,
,
где 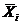 – среднее арифметическое i -й серии наблюдений:
– среднее арифметическое i -й серии наблюдений:
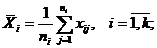
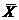 – общее среднее арифметическое всех
– общее среднее арифметическое всех 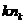 наблюдений:
наблюдений:
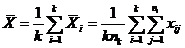 .
.
В качестве статистической характеристики для гипотезы  возьмем величину
возьмем величину
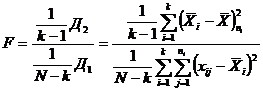 .
.
Если гипотеза 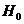 верна, то величина F имеет F -распределение Фишера – Снедекора с
верна, то величина F имеет F -распределение Фишера – Снедекора с 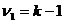 и
и 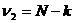 степенями свободы. Критическая область правосторонняя, т.е. ей принадлежат все значения статистической характеристики F, большие табличного значения
степенями свободы. Критическая область правосторонняя, т.е. ей принадлежат все значения статистической характеристики F, большие табличного значения 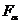 , для которого справедливо равенство
, для которого справедливо равенство 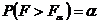 . Поэтому если
. Поэтому если 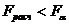 , то нет основания отвергать нулевую гипотезу
, то нет основания отвергать нулевую гипотезу 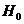 о равенстве средних. Число
о равенстве средних. Число 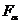 находим по таблице F -распределения для заданного уровня значимости
находим по таблице F -распределения для заданного уровня значимости 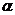 с
с 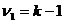 и
и 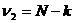 степенями свободы.
степенями свободы.
Схему применения дисперсионного анализа можно представить в виде табл. 2.10.
Т а б л и ц а 2.10
| Дисперсия | Сумма квадратов | Число степеней свободы | Средний квадрат |
| По факторам между сериями | 
| 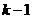
| 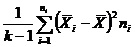
|
| Внутри серии | 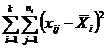
| 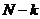
| 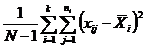
|
| Общая | 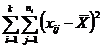
| 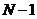
| 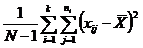
|
Таким образом, для выяснения взаимосвязи факторов сравнивают дисперсию по факторам с остаточной дисперсией по величине их отношения. В этом сравнении и заключается основная идея дисперсионного анализа.
Пример 2.2. Применим дисперсионный анализ для проверки существенности статистической связи между количеством мяса на душу населения (X, кг) и ценой за 1 кг мяса (Y, день. ед.):
X.... 10,03 11,44 20,19 20,25 23,50 24,49 24,98 27,05
Y.... 4,60 6,50 5,84 4,54 4,96 4,78 4,85 4,87
Для проверки гипотезы 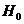 о существовании связи между изучаемыми признаками разобьем данные признаков по группам, использовав формулу (1.1) для определения величины группы, и построим корреляционную таблицу 2.11, где
о существовании связи между изучаемыми признаками разобьем данные признаков по группам, использовав формулу (1.1) для определения величины группы, и построим корреляционную таблицу 2.11, где 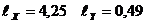
Т а б л и ц а 2.11
| Y | 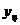
| X | 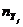
| ||||
| 10,03 - 14,28 | 14,28 - 18,53 | 18,53 - 22,78 | 22,78 - 27,03 | 27,03 - 31,28 | |||
| 4,53 – 5,03 5,03 – 5,52 5,52 – 6,01 6,01 – 6,50 | 4,785 5,275 5,765 6,255 | - - | - - - - | - - | - - - | - - - | - |
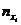
| - | - | n =8 |
Таким образом, мы сгруппировали исходную статистическую совокупность по переменным 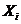 , i =
, i = 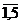 , для которых выделены
, для которых выделены 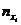 независимых наблюдений:
независимых наблюдений:
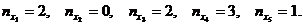
Принимая во внимание интерпретацию данных как совокупность переменных 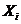 , i =
, i = 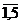 , с
, с 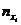 независимыми наблюдениями, нужно проверить гипотезу
независимыми наблюдениями, нужно проверить гипотезу 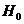 о равенстве математических ожиданий всех случайных величин
о равенстве математических ожиданий всех случайных величин 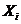 , i =
, i = 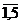 . Значения средних по выделенным пяти группам:
. Значения средних по выделенным пяти группам:
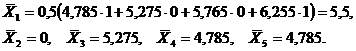
Результаты промежуточных расчетов сведены в табл. 2.12.
Т а б л и ц а 2.12
| Группы | Y | 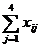
| 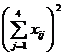
| 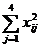
| |||
4,54 – 5,03
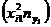 
| 5,03 – 5,52
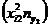
| 5,52 – 6,01
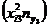
| 6,01 – 6,50

| ||||
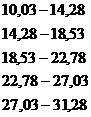
| 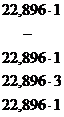
| 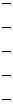
| 
| 
| 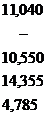
| 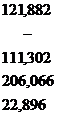
| 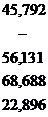
|
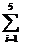
| 137,376 | - | 33,235 | 22,896 | 40,730 | 462,146 | 193,507 |
Тогда
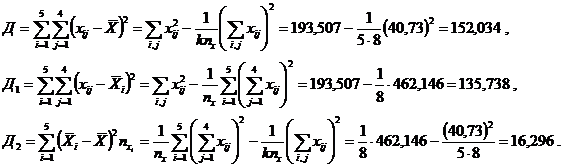
Составим соответствующую таблицу однофакторного дисперсионного анализа (табл. 2.13).
Т а б л и ц а 2.13
| Дисперсия | Сумма квадратов | Число степеней свободы | Средний квадрат |
| Внутри группы Между группами Общая | 135,738 16,296 152,034 | 45,246 4,074 21,719 |
Статистическая характеристика
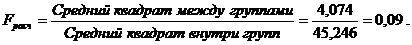
По таблице F -распределения находим  или
или 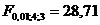 . Полученное значение
. Полученное значение 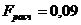 меньше обоих критических значений, т.е.
меньше обоих критических значений, т.е. 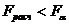 . Следовательно, расхождение в средней цене для выделенных четырех групп несущественно и не зависит от количества мяса на душу населения.
. Следовательно, расхождение в средней цене для выделенных четырех групп несущественно и не зависит от количества мяса на душу населения.
А это означает, что связь между изучаемыми факторами несущественна, т.е. с вероятностью 0,99 можно говорить об отсутствии связи между количеством мяса на душу населения и ценой за 1 кг.
Вопросы для самопроверки
1. Оценку какой вероятности позволяет сделать критерий 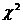 ?
?
2. Что составляет теоретическую основу дисперсионного анализа?
3. Изложите последовательность проверки объективности связи с помощью критерия 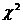 , дисперсионного анализа.
, дисперсионного анализа.
Задача. По данным, приведенным в табл. 2.14, проверьте гипотезу о взаимосвязи
энерговооруженности одного работника (X, л.с.) и валовой продукции на одного среднегодового работника сельского хозяйства (Y, день. ед.).
Т а б л и ц а 2.14
| X | Y | X | Y | X | Y | ||
| 32,339 28,310 29,600 26,095 33,322 28,136 31,287 29,773 | 26,876 30,187 36,886 33,707 31,772 28,109 33,722 | 29,331 38,050 29,160 29,118 29,356 27,125 28,331 |
2.3. Однофакторные регрессионные модели
Выбор формы однофакторной регрессионной модели. Для более углубленного исследования связей и взаимозависимости экономических явлений статистические методы, изученные в § 2.1, 2.2, дополняются функциями регрессии, которые выражают количественное соотношение между явлением-результатом и явлениями-причинами. Форма связи между экономическими явлениями выражается аналитическим уравнением, на основании которого определяются величины признака (явления), зависящие от фактора или факторов, принимаемых во внимание. При этом нужно определить такое математическое уравнение, которое наилучшим образом описывало бы характер исследуемого экономического процесса. Установление формы связи зависит от характера взаимосвязи исследуемых явлений и определяется тои наукой, к которой относятся изучаемые явления. Если изучается связь между факторным и результативным признаками, то форму этой связи можно определить из расположения точек на корреляционном поле или из корреляционной таблицы, в которой вычисляются средние результативного признака для каждой группы факторного признака:
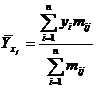 ,
,
где 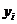 – значения середины интервалов ряда распределения Y;
– значения середины интервалов ряда распределения Y; 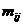 – частоты парных значений
– частоты парных значений 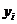 и
и 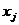 .
.
Для определения вида функции регрессии, соответствующей реальной форме зависимости, используется метод дисперсионного анализа, который позволяет оценивать линейность регрессии. Покажем, как реализуется метод дисперсионного анализа для случая линейной формы связи. Для этого предположим, что между исследуемыми признаками существует линейная зависимость 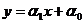 .
.
Сгруппируем всю совокупность наблюдений в виде таблицы:
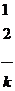
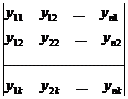
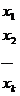 ,
,
где каждая строка соответствует определенному значению фактора X.
Для определения параметров 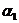 и
и 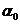 нужно минимизировать сумму
нужно минимизировать сумму
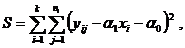
которую представим в виде
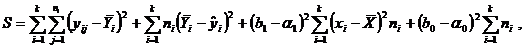
где 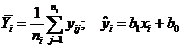 – эмпирическая линия регрессии. Это разложение приводит к дисперсиям:
– эмпирическая линия регрессии. Это разложение приводит к дисперсиям:
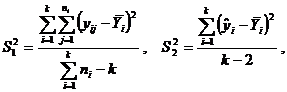
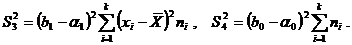
Дисперсии  – это вариации значений признака соответственно в пределах групп наблюдений и около линии регрессии;
– это вариации значений признака соответственно в пределах групп наблюдений и около линии регрессии; 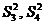 – вариации эмпирических коэффициентов по отношению к теоретическим.
– вариации эмпирических коэффициентов по отношению к теоретическим.
Для проверки гипотезы линейности связи между исследуемыми признаками составляется F -отношение:
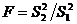 ,
,
которое подчиняется распределению Фишера – Снедекора с 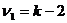 и
и 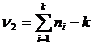 степенями свободы. И если вычисленное F -отношение меньше табличного для заданного уровня доверия, то гипотеза о линейности связи подтверждается.
степенями свободы. И если вычисленное F -отношение меньше табличного для заданного уровня доверия, то гипотеза о линейности связи подтверждается.
Смысл изложенного ясен. Если регрессия прямолинейная, то отклонения от нее следует считать случайными. Случайной при такой зависимости будет и та часть отклонений, которая приходится на различия между теоретической и эмпирической линиями регрессии. Теоретическая регрессия представляет то предельное положение, к которому стремится эмпирическая регрессия при увеличении числа наблюдений. Расхождение между ними обусловливается тем, что в эмпирической линии регрессии оказывается непогашенной некоторая часть случайных колебаний. Но это верно лишь тогда, когда теоретическая регрессия в виде прямой действительно правильно выражает форму связи. Если же это не так, то и отклонения эмпирической линии регрессии от теоретической прямой регрессии должны уже рассматриваться не как случайные, а как закономерное отражение кривизны регрессии. Сравнение этих отклонений с чисто случайной их величиной и должно дать ответ на поставленный вопрос о линейной регрессии.
Основные предпосылки применения метода наименьших квадратов в аппроксимации связей признаков социально-экономических явлений. Так как при построении регрессионной модели мы не можем охватить весь комплекс причин и учесть случайность, присущую в тои или иной степени причинному действию и определяемому им следствию, то в выражение функции регрессии необходимо ввести аддитивную составляющую – возмущающую переменную U, дающую суммарный эффект от воздействия всех неучтенных факторов и случайностей. Эмпирические значения Y можно вследствие этого представить в виде 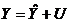 . Для нахождения параметров расчетных значений Y должны выполняться некоторые предпосылки (предположения). Эти предпосылки имеют общий характер, т.е. они не определяются объемом выборки и числом включенных в анализ переменных.
. Для нахождения параметров расчетных значений Y должны выполняться некоторые предпосылки (предположения). Эти предпосылки имеют общий характер, т.е. они не определяются объемом выборки и числом включенных в анализ переменных.
Наиболее существенными предположениями являются следующие.
1. Полагаем, что для фиксированных значений переменных 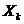 математическое ожидание возмущающей переменной
математическое ожидание возмущающей переменной 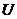 равно нулю:
равно нулю: 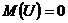 . Следовательно, средний уровень значений переменной Y определяется только функцией регрессии и возмущающая переменная не коррелирует со значениями регрессии:
. Следовательно, средний уровень значений переменной Y определяется только функцией регрессии и возмущающая переменная не коррелирует со значениями регрессии:
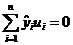 .
.
2. Дисперсия случайной переменной U должна быть для всех 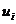 одинакова и постоянна:
одинакова и постоянна:  . Это свойство возмущающей переменной U называется гомоскедастичностью.
. Это свойство возмущающей переменной U называется гомоскедастичностью.
3. Значения случайной переменной U попарно независимы в вероятностном смысле: 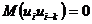 для
для 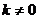 .
.
4. Число наблюдений должно превышать число параметров (n > m), иначе невозможна оценка этих параметров. Между факторными переменными не должно существовать строгой линейной зависимости, т.е. должна отсутствовать мультиколлинеарность между факторными переменными. При простой линейной регрессии это предположение сводится к условию 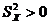 .
.
5. Переменные факторы не должны коррелировать с возмущающей переменной U, т.е. 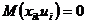 . Это значит, что рассматриваемая односторонняя зависимость переменной Y от
. Это значит, что рассматриваемая односторонняя зависимость переменной Y от
переменных 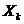 , а взаимосвязь отсутствует.
, а взаимосвязь отсутствует.
6. Возмущающая переменная распределена нормально. Предполагается, что переменная U не оказывает существенного влияния на переменную Y и представляет собой суммарный эффект от большего числа незначительных некоррелированных влияющих факторов.
Метод наименьших квадратов – один из наиболее распространенных методов оценивания неизвестных параметров регрессии по эмпирическим данным. Существуют и другие методы оценок параметров регрессии. Отметим, что при одних и тех же предположениях и одной и тои же функции регрессии различные способы оценивания приводят к разным оценкам параметров регрессии.
Задача регрессионного анализа состоит в нахождении истинных значений параметров, т.е. в определении соотношения между X и Y в генеральной совокупности. С помощью регрессионного анализа находят оценки параметров регрессии, наиболее хорошо согласующиеся с опытными данными. Разность между значениями параметров регрессии 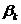 и их оценками
и их оценками 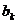 возникающая за счет оценивания на основе имеющихся в распоряжении данных, называется ошибкой оценки. При выборе метода оценивания регрессии пытаются найти такие оценки параметров регрессии, относительно которых с достаточно большей вероятностью можно утверждать, что они незначительно отличаются от истинного значения параметра
возникающая за счет оценивания на основе имеющихся в распоряжении данных, называется ошибкой оценки. При выборе метода оценивания регрессии пытаются найти такие оценки параметров регрессии, относительно которых с достаточно большей вероятностью можно утверждать, что они незначительно отличаются от истинного значения параметра 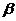 или что они являются несмещенными, состоятельными и эффективными.
или что они являются несмещенными, состоятельными и эффективными.
Состоятельность – важнейшее и минимально необходимое требование, предъявляемое к оценкам.
Если выполняются предпосылки 1 – 6, то оценки параметров регрессии, полученные методом наименьших квадратов, являются состоятельными, несмещенными и эффективными. Оценки, полученные методом наименьших квадратов, обладают наименьшей дисперсией. В этом смысле они представляют собой наилучшие линейные несмещенные оценки параметров теоретической регрессии.
Построение регрессионной прямой методом наименьших квадратов. Если, исходя из профессионально-теоретических соображений в сочетании с исследованием расположения точек на корреляционном поле или других соображений, предполагают линейный характер зависимости усредненных значений результативного признака, то эту зависимость выражают с помощью функции линейной регрессии, которая служит оценкой линейной функциональной связи между результативным и факторным признаками:
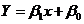 .
.
На результативный признак оказывает влияние и ряд других факторов. Чтобы элиминировать (сгладить) влияние этих факторов, нужно произвести выравнивание фактических величин Y на основании предположения, что между X и Y существует функциональная зависимость. При этом фактические значения Y заменяются значениями, вычисленными па формуле
 . (2.3)
. (2.3)
Так как все факторы, кроме фактора X, рассматриваются как постоянные средние величины и выражены параметрами  и
и 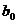 , то и сглаженные величины Y представляют собой средние
, то и сглаженные величины Y представляют собой средние 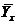 . Неизвестные параметры
. Неизвестные параметры  и
и 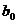 входящие в уравнение (2.3), определяются методом наименьших квадратов:
входящие в уравнение (2.3), определяются методом наименьших квадратов:
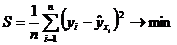 .
.
Величина S является функцией параметров  и
и 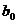 . Тогда, в силу необходимого условия экстремума, частные производные S по
. Тогда, в силу необходимого условия экстремума, частные производные S по  и
и 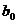 должны быть равны нулю:
должны быть равны нулю:
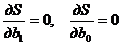 .
.
Выполнив преобразования и решив систему нормальных уравнений, получим:
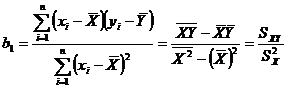 ,
,
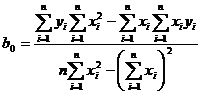 .
.
Параметр  называется коэффициентом регрессии. Он характеризует угол наклона эмпирической регрессии к оси Ox:
называется коэффициентом регрессии. Он характеризует угол наклона эмпирической регрессии к оси Ox: 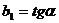 (рис. 2.3).
(рис. 2.3).
Коэффициент регрессии является мерой зависимости переменной Y от переменной X, т.е.  указывает, как в среднем изменяется значение переменной Y при изменении переменной X на одну единицу. Знак коэффициента регрессии определяет направление этого изменения.
указывает, как в среднем изменяется значение переменной Y при изменении переменной X на одну единицу. Знак коэффициента регрессии определяет направление этого изменения.
Отыскание значений коэффициента регрессии представляет большей практический интерес, если ставится вопрос о прогнозе изменений какого-либо показателя в связи с изменением того или иного условия. В частности, коэффициент регрессии используется для определения эластичности спроса и потребления.
В общем случае коэффициент эластичности представляет собой процентное изменение результативного признака при изменении факторного признака на один процент. Он вычисляется по формуле
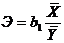 ,
,
где  – коэффициент регрессии;
– коэффициент регрессии; 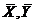 – средние значения соответственно факторного и результативного признаков.
– средние значения соответственно факторного и результативного признаков.
Например, коэффициент эластичности потребления выражает процентное изменение потребления или спроса на данный товар при изменении известных условий (дохода, цены и т.д.) на один процент.
Параметры  и
и 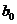 прямой регрессии – не безразмерные величины. Постоянная регрессии
прямой регрессии – не безразмерные величины. Постоянная регрессии 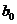 имеет размерность признака Y. Размерность коэффициента регрессии
имеет размерность признака Y. Размерность коэффициента регрессии  представляет собой отношение размерности результативного признака к размерности факторного признака.
представляет собой отношение размерности результативного признака к размерности факторного признака.
После вычисления оценок параметров регрессии  и
и 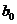 , а также средних значений
, а также средних значений 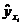 по формуле
по формуле 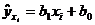 вычисляем остатки
вычисляем остатки
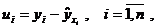
которые используются в качестве характеристики точности оценки регрессии или степени согласованности расчетных значений регрессии и наблюдаемых значений переменной Y. Для характеристики меры разброса фактических данных 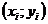 вокруг значений регрессии вычисляют дисперсию остатков:
вокруг значений регрессии вычисляют дисперсию остатков:
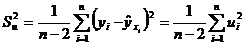 .
.
Геометрический смысл параметров прямой регрессии следует из рис. 2.2.
Используя дисперсию остатков, можно указать среднюю квадратичную ошибку коэффициента регрессии:
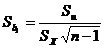 .
.
Как уже отмечалось, функция регрессии указывает, в какой степени изменяются значения результативного признака в соответствии с изменением факторного признака. Однако этого недостаточно для глубокого изучения их взаимосвязи. Нужно измерить еще интенсивность между изучаемыми факторами. Оценки, полученные с помощью уравнения регрессии, имеют точность тем большую, чем интенсивнее корреляция.
Измерение интенсивности корреляционной связи. Мы рассмотрели, как определяется форма связи между факторным и результативным признаками. Изучим теперь показатели интенсивности этой связи.
Вычислив дисперсию результативного признака 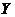 и воспользовавшись отклонениями величины
и воспользовавшись отклонениями величины 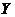 от средней величины
от средней величины 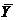 , получим показатель общей дисперсии
, получим показатель общей дисперсии 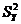 , характеризующей вариацию признака Y. Вычислим дисперсию
, характеризующей вариацию признака Y. Вычислим дисперсию 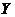 для каждого отдельного значения признака
для каждого отдельного значения признака 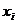 и воспользовавшись отклонениями данных значений
и воспользовавшись отклонениями данных значений 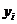 от значений, рассчитанных по уравнению линии регрессии, получим условную дисперсию
от значений, рассчитанных по уравнению линии регрессии, получим условную дисперсию 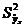 . Она меньше дисперсии
. Она меньше дисперсии 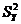 .
.
В качестве показателя интенсивности связи примем нормированное выражение разности этих дисперсий
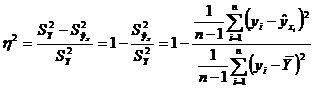
или
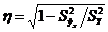 . (2.4)
. (2.4)
Этот показатель называется корреляционным отношением. При этом чем больше нормированная разность 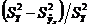 тем теснее связь, т.е. тем теснее фактические данные примыкают к линии регрессии. При функциональной связи все значения Y лежали бы на линии регрессии.
тем теснее связь, т.е. тем теснее фактические данные примыкают к линии регрессии. При функциональной связи все значения Y лежали бы на линии регрессии.
Средняя квадратичная ошибка корреляционного отношения
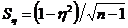 .
.
Корреляционное отношение можно вычислять также и по формуле
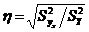 ,
,
где дисперсия
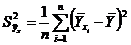
определяет вариацию величины 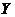 только вследствие изменения величин
только вследствие изменения величин 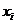 т.е. определяет отклонение средних величин
т.е. определяет отклонение средних величин 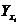 , найденных для каждого значения
, найденных для каждого значения 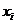 , от общей средней
, от общей средней 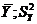 – общая дисперсия признака Y. Таким образом, корреляционное отношение выражает ту часть вариации, которую данный факторный признак составляет в общем действии всех условий вариации коррелируемого с ним другого признака. Но это и определяет тесноту связи, в которой находится признак Y с признаком X.
– общая дисперсия признака Y. Таким образом, корреляционное отношение выражает ту часть вариации, которую данный факторный признак составляет в общем действии всех условий вариации коррелируемого с ним другого признака. Но это и определяет тесноту связи, в которой находится признак Y с признаком X.
Корреляционное отношение используется для оценки интенсивности как прямолинейной, так и криволинейной формы связи. Однако оно применяется обычно при криволинейной связи. При прямолинейной связи общим показателем интенсивности является линейный коэффициент корреляции (просто коэффициент корреляции)
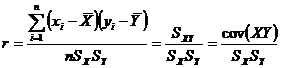 .
.
Коэффициент корреляции, так же как и корреляционное отношение, является безразмерной величиной, так как сравниваются не индивидуальные отклонения, а нормированные отклонения 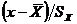 и
и 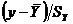 . Среднее произведение нормированных отклонений и дает коэффициент корреляции.
. Среднее произведение нормированных отклонений и дает коэффициент корреляции.
Степень интенсивности корреляционной связи можно определить из табл. 2.15.
Т а б л и ц а 2.15
| Корреляционная зависимость | Значение коэффициента корреляции |
| Слабая Умеренная Заметная Тесная Весьма тесная | 0,1 < r < 0,3, -0,3 < r < -0,1 0,3 < r < 0,5, -0,5 < r < -0,3 0,5 < r < 0,7, -0,7 < r < -0,5 0,7 < r < 0,9, -0,9 < r < -0,7 0,9 < r < 0,99, -0,99 < r < -0,9 |
Отметим, что коэффициент корреляции не отражает направление зависимости, т.е. он является функцией, симметричной относительно X и Y.
Средняя квадратичная ошибка коэффициента корреляции определяется по формуле
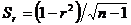 .
.
Наряду с коэффициентом корреляции и корреляционным отношением в математической статистике применяется коэффициент детерминации, отражающий, в какой мере функция регрессии определяется факторными признаками, содержащимися в ней.
Для определения коэффициента детерминации дисперсию, характеризующую рассеяние наблюдаемых значений переменной 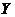 около ее среднего, разложим на две составляющие:
около ее среднего, разложим на две составляющие:

где 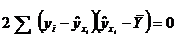 , так как прямая регрессии проходит через среднюю точку
, так как прямая регрессии проходит через среднюю точку 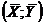 корреляционного поля.
корреляционного поля.
Дисперсия 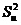 представляет собой ту часть общей дисперсии
представляет собой ту часть общей дисперсии
| <== предыдущая | | | следующая ==> |
| Структура и состав графической работы | | |
Date: 2015-07-17; view: 594; Нарушение авторских прав