
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Значения обратных функций для получения дискретного распределения
|
|
| i | |||||||
| xi | |||||||
| bi | 0,447 | 0,017 | 0,038 | 0,151 | 0,110 | 0,007 | 0,230 |
| gi | 0,447 | 0,464 | 0,502 | 0,653 | 0,763 | 0,770 | 1,000 |
Воспользуемся методом обратных функций. Сначала найдем сумму всех частот – получим S=291. После этого построим таблицу нормированных значений bi=xi/S (третья строка табл. 1). Далее рассчитаем значения дискретной функции по формуле: 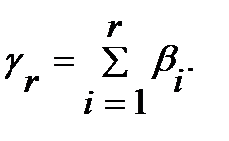
Полученные значения находятся в четвертой строке табл. 1.. Построим график дискретной функции (рис. 1.). Далее воспользуемся программой получения случайных величин, распределенных равномерно на отрезке (0,1), и каждый раз будем получать случайную величину pt, После этого выбор объекта с номером i осуществляется при выполнении соотношения
gi-1 < pt <= gi
 Получение дискретного распределения
Получение дискретного распределения
Моделирование непрерывной случайной величины
Для получения непрерывных случайных величин с заданным законом распределения, как и для дискретных величин, можно воспользоваться методом обратной функции. Если случайная величина Y имеет плотность распределения f(y), то распределение случайной величины
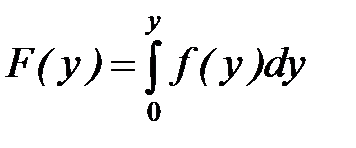
является равномерным на интервале (0,1). Чтобы получить число, принадлежащее последовательности случайных чисел {yi}, имеющих функцию плотности f(y), необходимо разрешить относительно yi уравнение
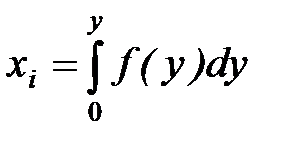
где xi - число, принадлежащее последовательности случайных чисел равномерно распределенных на интервале от (0,1).
Пример. Необходимо получить случайные числа с показательным законом распределения (например, интервалов времени между поступлениями заявок на обслуживание):
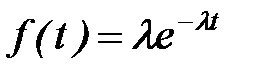 .
.
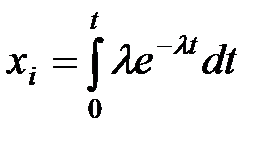
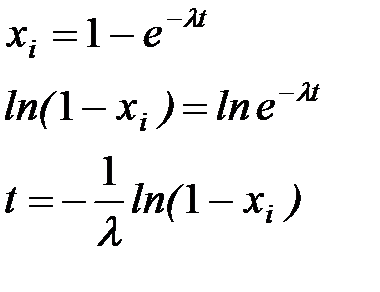
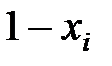 - случайное число, имеющее равномерное распределение на интервале (0,1). Тогда
- случайное число, имеющее равномерное распределение на интервале (0,1). Тогда
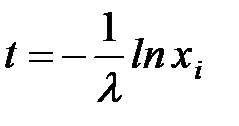
Этот способ получения случайных чисел с заданным законом распределения имеет ограниченную сферу применения, так как для многих законов распределения, встречающихся в практических задачах моделирования, интеграл не берется, т.е. приходится прибегать к численным методам решения, что увеличивает затраты вычислительных ресурсов на получение каждого числа; даже для случаев, когда интеграл берется в конечном виде получаются формулы, содержащие действия логарифмирования, извлечения корня и т.д., что также резко увеличивает затраты машинного времени на получение каждого случайного числа. Поэтому на практике часто пользуются приближенными способами преобразования случайных чисел, которые можно классифицировать следующим образом:
а) универсальные способы, с помощью которых можно получать случайные числа с законом распределения любого вида; б) неуниверсальные способы, пригодные для получения случайных чисел с конкретным законом распределения.
Рассмотрим приближенный универсальный способ получения случайных чисел, основанный на кусочной аппроксимации функции плотности.
Пусть требуется получить последовательность случайных чисел { yj } с функцией плотности fh(y), значения которой лежат в интервале (a,b). Разобъем интервал (a,b) на m интервалов (рис.5), и будем считать fh(y) на каждом интервале постоянной. Разбивать необходимо так, чтобы вероятность попадания случайной величины в любой интервал (ak, ak+1) была постоянной, т.е.:
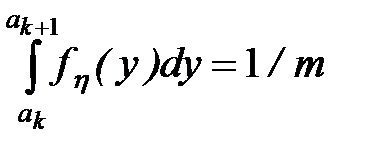
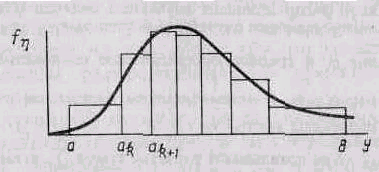
Кусочная аппроксимация функции плотности
В таком случае, алгоритм этого способа получения случайных чисел сводится к выполнению следующих действий:
1) Генерируется случайное равномерно распределенной число xi из интервала (0,1);
2) с помощью этого числа выбирается интервал (ak, ak+1);
3) генерируется число xi+1 ;
4) вычисляется случайное число yj =ak+ xi+1 (ak+1-ak) с требуемым законом распределения.
Рассмотрим пример применения способа преобразования последовательности равномерно распределенных случайных чисел {xi} в последовательность с заданным законом распределения {yi} на основе предельных теорем теории вероятностей. Такие способы ориентированы на получение последовательностей чисел с конкретным законом распределения, т.е. не являются универсальными.
Пример. Пусть требуется получить последовательность случайных чисел {yi}, имеющих нормальное распределение с математическим ожиданием m и средним квадратическим отклонением s:

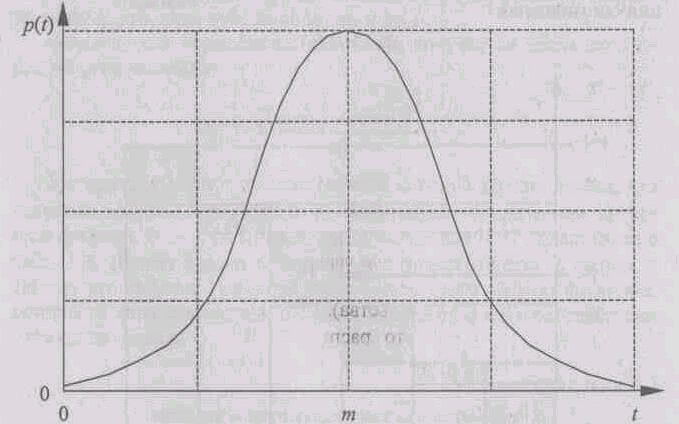
Вид нормального распределения
Будем формировать случайные числа tj в виде сумм последовательностей случайных чисел {xi}, равномерно распределенных на интервале от (0,1). Можно воспользоваться центральной предельной теоремой: Если X1 , X2,..., Xn - независимые одинаково распределенные случайные величины, имеющие математическое ожидание M(Xi)=a и дисперсию s2, то при N ® ¥ сумма 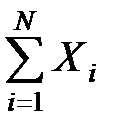 асимптотически нормальна с математическим ожиданием Na и средним квадратическим отклонением
асимптотически нормальна с математическим ожиданием Na и средним квадратическим отклонением 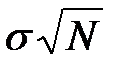 . Практически достаточно N=8¸12, а в простейших случаях - 4¸5. Преимущество этого способа - высокое быстродействие. Недостатком является игнорирование «хвостов» нормального распределения, которые могут уходить в обе стороны от величины т на расстояние, превышающее 6 s. Поэтому при проведении особо точных экспериментов применяются другие - более точные (но более медленные) способы. В современных системах имитационного моделирования обычно используются не менее двух программных датчиков случайных величин, распределенных по нормальному закону (их выбор осуществляется автоматически управляющей программой).
. Практически достаточно N=8¸12, а в простейших случаях - 4¸5. Преимущество этого способа - высокое быстродействие. Недостатком является игнорирование «хвостов» нормального распределения, которые могут уходить в обе стороны от величины т на расстояние, превышающее 6 s. Поэтому при проведении особо точных экспериментов применяются другие - более точные (но более медленные) способы. В современных системах имитационного моделирования обычно используются не менее двух программных датчиков случайных величин, распределенных по нормальному закону (их выбор осуществляется автоматически управляющей программой).
Треугольное распределение. Треугольное распределение применяется в тех случаях, когда о случайной величине ничего неизвестно, кроме наиболее вероятного значения и диапазона возможных значений этой случайной величины (рис. 3).
f(x)
f(С)
Date: 2015-07-17; view: 569; Нарушение авторских прав