Оптимизация компенсации реактивной мощности

При проектировании систем электроснабжения промышленного предприятия компенсация реактивной мощности позволяет уменьшить суммарные затраты на элементы электрической сети промышленного предприятия и сети электрической системы 3_{å с}, требуя дополнительных затрат на источники реактивной мощности 3_{å и}. Оптимальное соотно­шение между затратами этих двух видов соответствует условию

Функция суммарных затрат, соответствующая оптимальной степени компенсации, достаточно пологая. Поэтому можно говорить о некото­рой области различных степеней компенсации реактивной мощности, удовлетворяющих условию (11.17). Выбор степени компенсации внут­ри найденной области производится не по экономическим (ввиду их практической неэкономичности), а по техническим условиям, напри­мер по условиям обеспечения регулирования напряжения в системе электроснабжения. Под рациональной компенсацией реактивной мощ­ности в дальнейшем будем понимать выбор видов, мест размещения и располагаемой мощности источников реактивной мощности с точностью, достаточной для технико-экономических расчетов при проектировании.

В качестве исходных данных принимают конфигурации схемы си­стемы электроснабжения, активные и реактивные мощности нагрузок узлов сети, виды и места возможной установки источников реактив­ной мощности.

Для определения суммарных затрат на передачу реактивной мощ­ности по электрической сети промышленного предприятия примем обозначения: р_{н i}, Q_Нi - активная и реактивная мощности нагрузки в i -м узле сети; D Q_i - потери реактивной мощности в элементе, от-

несенные к i-му узлу сети; Q_иi - мощность источника реактивной мощности, предполагаемого к установке в i-м узле сети. Если в узле установка компенсирующего устройства не предполагается, то мощ­ность источника Q_и для этого узла принимается равной нулю; Р_bi, Q_bi — активная и реактивная мощности, передаваемые по элементам электрической сети, соответствующим i- ветви схемы; с_i — коэф­фициент линеаризации.

Суммарные расчетные затраты на передачу реактивной мощности по электрической сети промышленного предприятия можно пред­ставить в виде

Активная мощность в каждом из узлов сети равна соответствующей мощности нагрузки в том узле сети: Р_yi = P_Hi. Реактивная мощность в каждом из узлов сети Q_yi = Q_Hi + DQ_i – Q_иi.

Потери реактивной мощности в элементе сети, отнесенные в виде реактивных нагрузок D Q_i к начальным узлам этих элементов, опре­деляются формулами (11.15), (11.16). Потери реактивной мощности в элементе сети зависят от реактивных мощностей, протекающих по этим элементам, т. е. от не известной пока расстановки компенсирую­щих устройств.

Суммарные затраты на передачу реактивной мощности можно выра­зить в виде функции, переменными которой являются мощности Q_иi источников реактивной мощности в системе электроснабжения:

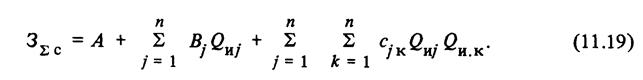
Первая составляющая функции 3_åc является постоянной частью затрат на передачу реактивной мощности. Она однозначно выражается через исходные данные задачи о компенсации реактивной мощности:

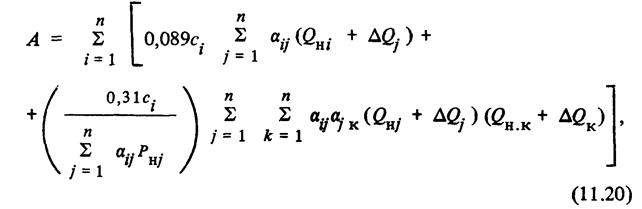
где a_ij = 1, если i -я ветвь принадлежит пути до j -го узла, и а_ij = 0 в про­тивном случае.

Вторая составляющая линейно зависит от реактивных мощностей источников Q_Иj:

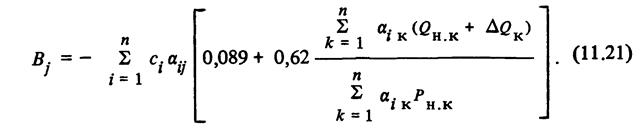
Третья составляющая является квадратичной формой от реактивных мощностей источников Q_иj:

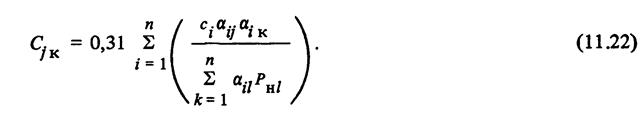
Таким образом, затраты на передачу реактивной мощности по эле­ментам электрической сети промышленного предприятия являются квадратичной функцией от мощности всех источников реактивной мощности, установленных в системе электроснабжения предприятий.

Суммарные затраты на источники в системе электроснабжения промышленных предприятий

где Q_Иi — реактивная мощность источника, предполагаемого к уста­новке в i -м узле промышленной сети. Если в узле источник реактив­ной мощности устанавливать не нужно, то соответствующая мощность полагается равной нулю; С_{и1 i}, C_{H2 i} - коэффициенты, характеризую­щие конкретный вид источника реактивной мощности.

Источники реактивной мощности электрической системы при реше­нии задачи о компенсации реактивной мощности в системе электроснаб­жения промышленного предприятия можно заменить одним эквива­лентным источником, который расположен в нулевом (балансирующем) узле. Затраты на эквивалентный источник должны отражать затраты на производство и передачу реактивной мощности до точки присоедине­ния системы электроснабжения промышленного предприятия к элект­рической системе. Поскольку затраты на генерацию и на передачу ре­активной мощности можно выразить в виде квадратичной функции от реактивной мощности, то и затраты на эквивалентный источник

реактивной мощности электрической системы также можно выра­зить в виде квадратичной функции.

Задачу об оптимальной компенсации реактивной мощности в си­стеме электроснабжения промышленного предприятия можно сфор­мулировать как задачу математического программирования: опреде­лить минимум целевой функции, соответствующей суммарным за­тратам на производство и передачу реактивной мощности в системе электроснабжения

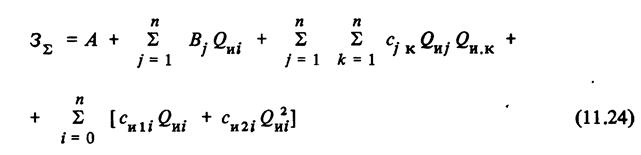
при выполнении баланса реактивной мощности

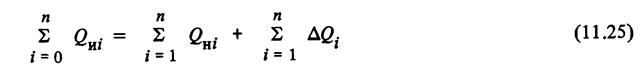
и обычных граничных условиях Q_ui ³ 0 (i = 1, 2,..., n). Граничные условия вытекают из физической сущности задачи: мощность ком­пенсирующих устройств не может быть отрицательной.

Переменные задачи — это мощности компенсирующих устройств Q_Иi. Поскольку целевая функция задачи является квадратичной функцией переменных, а балансовое условие — линейной функцией, это — задача квадратичного программирования. Оптимальная программа задачи соответствует оптимальной мощности компенсирующих устройств в системе электроснабжения Q_иiопт (i = 1, 2,..., n), опти­мальной реактивной мощности, передаваемой из электрической си­стемы (Q _и.опт), и минимальным суммарным затратам на производ­ство и передачу реактивной мощности 3_åmin.

Решение возможно на основе итерационного процесса расчета. Вна­чале определяются потери реактивной мощности в элементах элект­рической сети при предположении, что коэффициент мощности для всех элементов сети равен 0,92-0,95. Далее осуществляется расчет оптимального размещения компенсирующих устройств и расчет рас­пределения потоков реактивной мощности по элементам сети. Затем производится уточнение потерь реактивной мощности и новый расчет оптимального распределения компенсирующих устройств. Этот итера­ционный процесс быстро сходится, в результате чего определяются потери реактивной мощности и оптимальное размещение компенсирую­щих устройств.

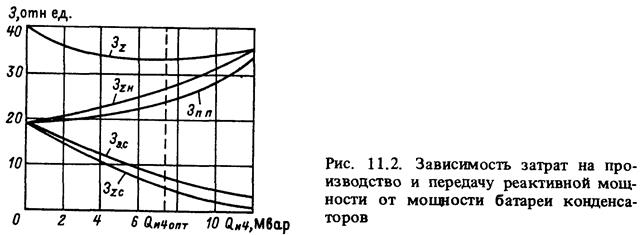
Зависимость затрат на производство и передачу реактивной мощно­сти от мощности батарей конденсаторов приведена на рис. 11.2. В ос­нову положена оптимальная степень компенсации реактивной мощно­сти системы электроснабжения промышленного предприятия (см. рис. 1.1), упрощенно представленной: на 6УР — двухцепной воздушной ЛЭП 110 кВ длиной 10 км, на 5УР — главной понизительной подстан­цией 110/10 кВ (трансформатор T-4); вся нагрузка распределяется от ГПП через Т-6 — цеховые подстанции ЗУР 10/0,4 к В, присоединенные непосредственно к ГПП кабелями длиной 0,5 км марки СБ, проложен­ными в траншее (анализ задачи с точки зрения информационного отбо­ра хорошо иллюстрирует ее условность).

На рисунке приведены зависимости от мощности батареи конденса­торов Q _и4 суммарных затрат з_å, их основных составляющих 3_åc, З_иå, а также затрат на производство и передачу реактивной мощности в электрической системе до 6УР - точки присоединения системы элект­роснабжения промышленного предприятия (З_эс = З_и0) - и затрат на производство и передачу реактивной мощности непосредственно в си­стеме электроснабжения промышленного предприятия 3_п.п = 3_åс + 3_и4.

При возрастании мощности батареи конденсаторов на шинах 0,4 кВ цеховых ТП Q _и4 увеличиваются затраты на источник реактивной мощ­ности З_иå и уменьшаются затраты на передачу реактивной мощности по элементам электрической сети 3_åc. Одновременно увеличиваются затраты на производство и передачу реактивной мощности непосред­­ственно в системе электроснабжения З_п.п и уменьшаются затраты 3_э.с на производство и передачу реактивной мощности в электрической системе до 6УР. Из этого можно заключить, что компенсация реактив­ной мощности для самого промышленного предприятия невыгодна, так как З_п.п возрастают. Она выгодна для электрической системы З_э.с уменьшаются. Минимум общегосударственных затрат 3_э.с имеет место при вполне определенной мощности компенсирующих устройств.

Функция суммарных затрат в окрестности оптимальной степени компенсации достаточно пологая. Поэтому для инженерных расчетов

с точностью 10% существует область рациональной мощности компен­сирующих устройств. Для данной задачи область 5% лежит в пределах Q_{И 4} = 4 ¸ 11 Мвар (или cos j₄ = 0,89 ¸ 0,997). Выбор компенсирующих устройств внутри этой области может производиться уже не по эконо­мическим, а по техническим условиям.

Date: 2015-06-11; view: 1738; Нарушение авторских прав