
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Технологическая надежность. Внезапные отказы. Модель экспоненциального распределения времени безотказной работы. Основное соединение элементов при расчете надежности ИЭС
|
|
- технологической надежности - 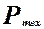 , характеризующей достижимый на заданный период эксплуатации уровень вероятности «физической» безотказности ИЭС (подсистем) в результате воздействия внутренних дефектов изготовления, внезапных внешних нагрузок или факторов постепенного износа.
, характеризующей достижимый на заданный период эксплуатации уровень вероятности «физической» безотказности ИЭС (подсистем) в результате воздействия внутренних дефектов изготовления, внезапных внешних нагрузок или факторов постепенного износа.
Внезапные отказы, характеризующиеся скачкообразным изменением значений одного или нескольких основных параметров системы (устройства, узла и т. п.).
Экспоненциальное распределение СВ описывает схему возникновения внезапных, мгновенных повреждений устройств. В этом случае отказ является следствием внешних условий эксплуатации (ударных нагрузок, температурных условий и т.п.) и не зависит от состояния самого устройства.
Любой элемент ИЭС имеет ограниченную «прочность». Поэтому имеется некоторая предельная нагрузка Sпр, которую система способна выдержать без отказа. Если же нагрузка S(t) превзойдет Sпр, то произойдет мгновенный отказ.
при экспоненциальном распределении времени безотказной работы нет смысла прибегать к профилактическим мерам типа предварительной замены элементов или их периодического ремонта.
Единственный путь повышения надежности состоит в конструктивном улучшении системы (элемента) или в снижении действующих нагрузок.
Количественно экспоненциальное распределение СВ характеризуется:
- вероятностью безотказной работы:
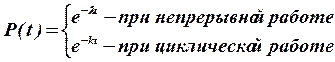 ;
;
- интенсивностью возникновения отказов, 1/ч:
- текущее время
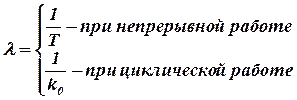 ;
;
- матожиданием времени безотказной работы, ч:
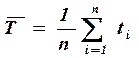 ,
,
где k, k0 – соответственно количество текущих и «безотказных» включений (циклов) объекта, шт; t – рассматриваемый период времени работы объекта, ч; n – число измерений (испытаний) объекта, шт.
8. Технологическая надежность. Постепенные отказы. Модели γ распределения, нормального и логнормального нормального распределения времени безотказной работы. Параметр смещения.
- технологической надежности - 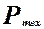 , характеризующей достижимый на заданный период эксплуатации уровень вероятности «физической» безотказности ИЭС (подсистем) в результате воздействия внутренних дефектов изготовления, внезапных внешних нагрузок или факторов постепенного износа.
, характеризующей достижимый на заданный период эксплуатации уровень вероятности «физической» безотказности ИЭС (подсистем) в результате воздействия внутренних дефектов изготовления, внезапных внешних нагрузок или факторов постепенного износа.
Гамма- распределение времени безотказной работы описывает схему непрерывного, постепенного износа, при котором отказ не наступает вследствие первого же повреждения, а является следствием накопления повреждений. Каждое из этих повреждений происходит по схеме мгновенного повреждения.
Нормальное распределение вероятности безотказной работы описывает схему длительного «естественного» старения. В этом случае отказы являются следствием накопления повреждений при постоянной скорости износа и однородном начальном качестве объектов.
При таких начальных условиях большая часть отказов наблюдается в течение конечного периода работы объекта. Ему подчиняются такие случайные величины, как погрешности измерения, погрешности изготовления и др. нормальное распределение базируется на стандартной табулированной функции Лапласа. Иногда считают, что износ любого вида (любое естественное старение) приводит к нормальному распределению времени безотказной работы.
Количественно нормальное распределение СВ описывается:
- вероятностью безотказной работы:
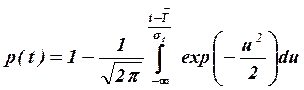 ; (4.9)
; (4.9)
- матожиданием времени безотказной работы, ч;
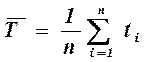 ; (4.10)
; (4.10)
- среднеквадратичным отклонением времени безотказной работы, ч:
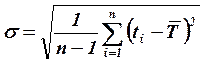
| (4.11) |
- плотность нормального распределения.
Кривые плотности нормального распределения симметричны и имеют ветви, уходящие в сторону Т = +  и Т = -
и Т = -  (рис. 4.4). Таким образом, нормальное распределение задано на всей временной шкале.
(рис. 4.4). Таким образом, нормальное распределение задано на всей временной шкале.
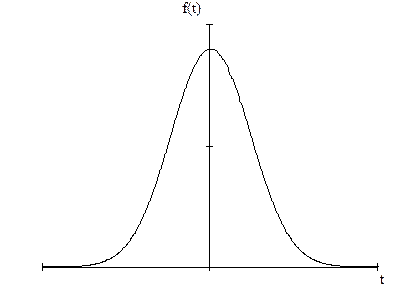
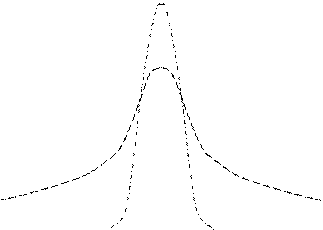
Рис. Плотность нормального распределения.
Логнормальное распределение описывает появление усталостных отказов, отказов вследствие износа и широко применяется на практике. Для логнормального закона характерна асимметрия (вершина кривой плотности лежит левее математического ожидания), т.е. большая часть отказов к моменту средней наработки уже произойдет. Значит t > 0 и в отрицательной области не существует. Асимметрия более ощутима при больших значениях дисперсии s.
Количественно логнормальное распределение СВ описывается:
- вероятностью безотказной работы:
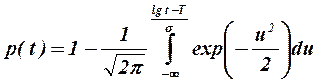 ; (4.12)
; (4.12)
- матожиданием времени безотказной работы, ч:
 ; (4.13)
; (4.13)
- среднеквадратичным отклонением времени безотказной работы, ч:
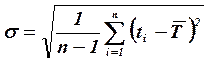 ; (4.14)
; (4.14)
- плотность логнормального распределения (рис. 4.6).
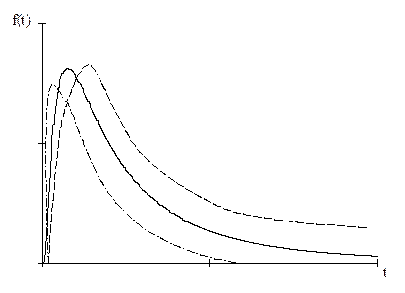
Рис. Плотность логнормального распределения
9. Понятие величины накопления повреждений до отказа r. Условие применимости различных законов распределения времени безотказной работы при расчете технологической надежности. Физический подход к определению технологической надежности ИЭС.
Физический подход к определению технологической надежности ИЭС
В технике расчет надежности сложных систем производится статистическим методом на основе классических или производных законов распределения при котором среднее время безотказной работы (наработка на отказ) Т, среднеквадратичное отклонение Ϭ определяется непосредственно обработкой статданных испытаний.
Величину накопления повреждений до отказа определяют:
В случае ИЭС такой метод не применим, так как такие данные отсутствуют, те значения параметров, входящих в законы распределения, нужно искать другим способом.
Это и составляет сущность физического подхода к расчету надежности.
Сведения об ИЭС
Технологическая схема
Условия эксплуатации
Справочные сведения
Данные по отдельным элементам системы
Данные по эксплуатации вентиляционных систем
Математическое описание
(законы распределения + граничные условия)
Перечень физических факторов износа
Расчет Р()
- выбор закона распределения
- определение Р(t)
- период жизненного цикла
Основной задачей, которую нужно решить для полноценного использования математического описания является расчет величины для характерных в случае эксплуатации ИЭС факторов износа (причин отказов).
Классификация факторов износа ИЭС
Коррозионный адгезионный абразивный усталостный
износ износ износ износ
коррозия в газах коррозия в растворах коррозия в твердой фазе
газовая коррозия электрохимическая в грунтах
при повышенной коррозия в каналах
температуре
атмосферная коррозия при неравномерной аэрации
местная общая контактная
Коррозия – процесс окисления железа, приводящий к возникновению сквозных отверстий.
Коррозия в газах при повышенной температуре.
Величины накопления повреждения до отказа r, равной:
r = M / y, (4.4)
где М - предельный уровень износа; у - приращение износа за каждое повреждение. При оценке величины r размерности при М и у должны быть одинаковы.
Оценка r предполагает использование дискретной модели рассмотрения отказа. Значения r определяют опытным путем и, как правило, принимают в виде целых чисел.
Исследования различных авторов показывают, что численные значения r при 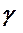 - распределении времени безотказной работы находятся в пределах:
- распределении времени безотказной работы находятся в пределах:
1 < r < 12.
Гамма- распределение СВ количественно характеризуется:
- вероятностью безотказной работы:
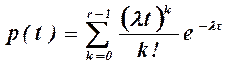 ; (4.5)
; (4.5)
- интенсивностью возникновения отказов, 1/ч:
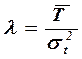 ; (4.6)
; (4.6)
- матожиданием времени безотказной работы, ч:
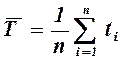 ; (4.7)
; (4.7)
- среднеквадратичным отклонением времени безотказной работы, ч:
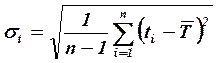 , (4.8)
, (4.8)
- плотность.
10. Технологическая надежность. Распределение Вейбулла- Гнеденко: область применения, характеристика параметров.
- Технологической надежности - 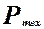 , характеризующей достижимый на заданный период эксплуатации уровень вероятности «физической» безотказности ИЭС (подсистем) в результате воздействия внутренних дефектов изготовления, внезапных внешних нагрузок или факторов постепенного износа.
, характеризующей достижимый на заданный период эксплуатации уровень вероятности «физической» безотказности ИЭС (подсистем) в результате воздействия внутренних дефектов изготовления, внезапных внешних нагрузок или факторов постепенного износа.
Данное распределение используется для описания времен жизни электронных устройств, механических систем и даже некоторых финансовых задач и учитывает не только закон распределения СВ, но и количество элементов в системе. Его целесообразно применять при оценке надежности системы (подсистемы):
- при наличии в системе значительного числа одинаковых или близких по конструкции элементов;
- примерно одинаковых эксплуатационных условиях, в которых находятся элементы, определяющие время безотказной работы системы (например, лопатки рабочего колеса вентилятора);
- параллельном действии и независимости причин, определяющих возможность отказа системы.
Переход от одной функции распределения СВ к другой прежде всего характеризует параметр формы В (рис. 4.7). Так, в частности:
- при В < 1 распределение СВ имеет вид экспоненциального закона;
- при 1 < B < 2..3 распределение СВ является переходным, близким к 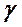 - распределению;
- распределению;
- при В = 5 распределение СВ имеет вид нормального закона.
|
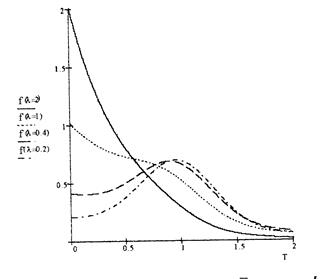
Рис. Плотность распределения Вейбулла—Гнеденко
Параметр положения (сдвига)С зависит от минимальной наработки, в течение которой в системе не будут наблюдаться отказы. Поэтому параметр С зависит от той фазы жизненного цикла технической системы, на этапе которой производится оценка надежности ее работы, в частности:
- зона приработки аппроксимируется распределением Вейбулла-Гнеденко с параметром положения c<1;
- зона установившегося нормального износа характеризуется параметром положения c=1;
- зона катастрофического износа моделируется распределением с параметром положения c>1.
В общем можно утверждать, что чем больше параметр С, тем выше безотказность технической системы.
Параметр масштабаА определяется из двухпараметрического (учитывающего только параметры А и В) распределения Вейбулла-Гнеденко, в котором параметр положения (сдвига) принят равным С = 0.
При построении для такого распределения серии кривых, соответствующих разным значениям параметра формы В, все кривые пересекаются в одной точке, которая носит название характеристического времени жизни системы и определяет момент, когда отказало 63,2 % выборки. Эта точка и будет равна соответствующему параметру масштаба А.
При этом вероятность безотказной работы, соответствующая значению параметра масштаба А, составляет:
Р(t) = 1 - 0,632 = 0,368.
11. Ориентировочный расчет технологической надежности ИЭС: область применения, исходные данные, последовательность расчета.
Ориентировочный расчет предполагает оценку и прогноз уровня надежности ИЭС и ее объектов на базе физического подхода при проведении научных исследований и проектировании технических решений ИЭС. Для его реализации достаточно знать структуру ИЭС, виды входящих в нее объектов и их количество. При этом делают основные допущения:
- все объекты ИЭС работают в номинальном (нормальном) режиме, предусмотренном техническими условиями;
- все объекты ИЭС работают одновременно;
- отказы объектов ИЭС являются событиями случайными и независимыми;
- интенсивности возникновения отказов объектов ИЭС постоянны в течение всего времени их работы.
В этом случае последовательность определения надежности ИЭС включает определение:
1) основного соединения элементов ИЭС: структуры системы, перечня ее подсистем, видов и количества входящих в них объектов. Степень детализации объектов может быть различной и определяется условиями поставленной задачи. Так, для расчета и оценки надежности подсистем ИЭС по защите воздуха достаточным будет их представление в виде отдельных сборочных элементов: устройство, электродвигатель, вентилятор, насос, воздуховод и т.п. Если же поставленная задача предполагает оптимизацию конструкции отдельных элементов, то деление на объекты должно доходить до уровня отдельных сборочных единиц, узлов и деталей;
2) типов объектов, входящих в основное соединение элементов ИЭС и их числа;
3) видов надежности: технологической или санитарно-гигиенической;
4) периода времени, за который необходимо произвести оценку надежности работы ИЭС;
5) величины накопления повреждений до отказа объектов различных типов, исходя из основных физических предпосылок возникновения отказа;
6) величины интенсивности возникновения отказов объектов различных типов с учетом данных о продолжительности межремонтных периодов работы систем;
7) закона распределения случайной величины, который в рассматриваемый период жизненного цикла описывает надежность объектов различных типов;
8) численных значений вероятности безотказной работы объектов в рамках каждого типа и расчетный уровень надежности по данному типу объектов в целом. В случаях, когда процесс износа начинается спустя некоторое время 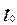 с начала эксплуатации объекта, необходимо учесть
с начала эксплуатации объекта, необходимо учесть 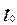 - параметр смещения (
- параметр смещения (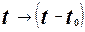 );
);
9) численных значений вероятностей безотказной работы подсистем ИЭС через расчетные уровни надежности составляющих их типов объектов;
10) численного значения вероятности безотказной работы ИЭС в целом через расчетные уровни надежности составляющих ее подсистем.
Таким образом, ориентировочный расчет помимо определения надежности ИЭС позволяет определить рациональный состав ее объектов и наметить пути повышения ее надежности на стадии проектирования.
12. Окончательный расчет технологической надежности ИЭС: область применения, исходные данные, последовательность расчета.
Окончательный расчет надежности ИЭС выполняется тогда, когда известны реальные режимы работы объектов в рамках ОС и статистически обработанные данные о времени их безотказной работы, полученные в результате лабораторных, промышленных испытаний или непосредственно при эксплуатации. При этом необходимо учесть следующее:
- фактические режимы работы входящих в ИЭС объектов могут достаточно сильно отличаться от номинальной величины. Речь идет о внешних воздействиях (окружающей температуре и скорости ее изменения, влажности) и нагрузках (механических перегрузках, вызванных вибрацией, ударами и т.п.) на объекты ИЭС;
- в течение рассматриваемого интервала времени работы объектов величина интенсивности возникновения отказов может быть не постоянной.
Выполнение окончательного расчета критериев надежности ИЭС возможно только при наличии данных о:
- коэффициентах нагрузки на отдельные объекты;
- зависимости интенсивности возникновения отказов (времени безотказной работы) отдельных объектов ИЭС от основных технологических параметров их работы. Эти зависимости обычно приводятся в виде поправочных коэффициентов к интенсивности возникновения отказов.
В этом случае последовательность расчета надежности ИЭС включает определение:
1) основного соединения элементов ИЭС, участвующего в расчете надежности с разбивкой его по режимам работы;
2) типов объектов (с учетом режимов работы), входящих в ОС элементов ИЭС и их числа;
3) видов надежности: технологической или санитарно-гигиенической;
4) периода времени, за который необходимо произвести оценку надежности работы ИЭС;
5) величины накопления повреждений до отказа объектов различных типов с использованием статистических данных о времени их безотказной работы;
6) величины интенсивности возникновения отказов объектов различных типов. Если в течение рассматриваемого периода времени объект имел непостоянную интенсивность отказов, но существовали четко выраженные временные интервалы, в течение которых интенсивность возникновения отказов была практически постоянна, то значение номинальной интенсивности возникновения отказов равна средневзвешенной величине:
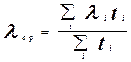 .
.
В общем случае интенсивность возникновения отказов объектов при их эксплуатации в реальных условиях должна учитывать поправочные коэффициенты на внешние воздействия (температуру, влажность) -  и внешние нагрузки, главным образом механические -
и внешние нагрузки, главным образом механические - 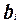 :
:
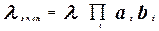 ; 7) закона распределения случайной величины, который в рассматриваемый период жизненного цикла описывает надежность объектов различных типов;
; 7) закона распределения случайной величины, который в рассматриваемый период жизненного цикла описывает надежность объектов различных типов;
8) численных значений вероятности безотказной работы объектов в рамках каждого типа и расчетный уровень надежности в рамках данного типа в целом;
9) численных значений вероятностей безотказной работы подсистем ИЭС через расчетные уровни надежности составляющих их типов объектов;
10) численного значения вероятности безотказной работы ИЭС в целом через расчетные уровни надежности составляющих ее подсистем.
Date: 2015-07-17; view: 1042; Нарушение авторских прав