Характеристики сигналів

1. Тривалість сигналу (час передачі) Т _с - інтервал часу, протягом якого існує сигнал.
2. Ширина спектра F _c - діапазон частот, в межах яких зосереджена основна потужність сигналу.
3. База сигналу - твір ширини спектру сигналу на його тривалість.
4. Динамічний діапазон D _c - логарифм відношення максимальної потужності сигналу - P _max до мінімальної - P _{min (мінімально-розрізни-травня} на рівні перешкод):
D _c = log (P _max / P _min).
У виразах, де може бути використані логарифми з будь-якою підставою, підстава логарифма не вказується.
Як правило, основу логарифма визначає одиницю виміру (наприклад: десятковий - [Бел], натуральний - [Непер]).
5. Обсяг сигналу визначається співвідношенням V _c = T _c F _c D _c.
6. Енергетичні характеристики: миттєва потужність - P (t); середня потужність - P _СР і енергія - E. Ці характеристики визначаються співвідношеннями:
P (t) = x ² (t); 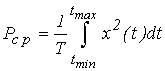; 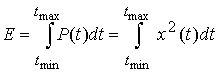(1)
де T = t _max - t _min.

Де́льта-фу́нкция (или δ-функция, δ-функция Дирака, дираковская дельта, единичная импульсная функция) — обобщённая функция, которая позволяет записать точечное воздействие, а также пространственную плотность физических величин (масса, заряд, интенсивность источника тепла, сила и т. п.), сосредоточенных или приложенных в одной точке.

Ортогональний базис — базис, складений з попарно ортогональних векторів.

Ортонормований базис задовольняє ще й умові одиничності норми всіх його елементів. Тобто це ортогональний базис з нормованими елементами.

Перетворення безперервних сигналів в дискретні

Дискретизация (от лат. discretio — «различать», «распознавать») — преобразование непрерывной функции в дискретную. Также: Преобразование непрерывного информационного множества аналоговых сигналов в дискретное множество называется дискретизацией или квантованием по уровню (ср. «Квантование по времени»).

Квантува́ння (англ. quantization, нім. Quantisierung f, Quantelung f) — дія, перетворення якоїсь величини з неперервною шкалою значень на величину з дискретною шкалою значень (наприклад, К. енергії частинок, К. сигналів). Наприклад, операція перетворення сигналу, при якій здійснюється його дискретизація за рівнем чи за часом або водночас і за рівнем, і за часом.

Теоре́ма Коте́льникова (в англоязычной литературе — теорема Найквиста) гласит, что, если аналоговый сигнал x(t) имеет ограниченный спектр, то он может быть восстановлен однозначно и без потерь по своим дискретным отсчётам, взятым с частотой не менее удвоенной максимальной частоты спектра Fmax:

fдискр \ge {2 \cdot F_{max}}

Інформаційні характеристики джерела повідомлень та каналів зв’язку

Отже, продуктивність джерела інформаціївизначається середньою кількістю інформації, що виробляється джерелом за одиницю часу.

Кодування інформації при передаванні дискретним каналом зв’язку

Алгоритм Шеннона — Фано — один из первых алгоритмов сжатия, который впервые сформулировали американские учёные Шеннон и Роберт Фано. Данный метод сжатия имеет большое сходство с алгоритмом Хаффмана, который появился на несколько лет позже и является логическим продолжением алгоритма Шеннона. Алгоритм использует коды переменной длины: часто встречающийся символ кодируется кодом меньшей длины, редко встречающийся — кодом большей длины. Коды Шеннона — Фано префиксные, то есть никакое кодовое слово не является префиксом любого другого. Это свойство позволяет однозначно декодировать любую последовательность кодовых слов.

Алгоритм Хаффмана — жадный алгоритм оптимального префиксного кодирования алфавита с минимальной избыточностью. Был разработан в 1952 году аспирантом Массачусетского технологического институтаДэвидом Хаффманом при написании им курсовой работы. В настоящее время используется во многих программах сжатия данных.

В отличие от алгоритма Шеннона — Фано, алгоритм Хаффмана остаётся всегда оптимальным и для вторичных алфавитов m₂ с более чем двумя символами.

Теорема Шеннона — Хартли в теории информации — применение теоремы кодирования канала с шумом к архетипичному случаю непрерывного временно́го аналогового канала коммуникаций, искажённогогауссовским шумом. Теорема устанавливает шенноновскую ёмкость канала, верхнюю границу максимального количества безошибочных цифровых данных (то есть, информации), которое может быть передано по такой связи коммуникации с указанной полосой пропускания в присутствии шумового вмешательства, согласно предположению, что мощность сигнала ограничена, и гауссовский шум характеризуется известной мощностьюили спектральной плотностью мощности. Закон назван в честь Клода Шеннона и Ральфа Хартли.

Ко́ды Хэ́мминга — вероятно, наиболее известный из первых самоконтролирующихся и самокорректирующихся кодов. Построены применительно к двоичной системе счисления. Позволяет исправлять одиночную ошибку (ошибка в одном бите) и находить двойную^[1].

Припустимо, потрібно передати повідомлення m завдовжки 9 символів. Розмістимо символи повідомлення у вигляді матриці, додавши до кожного рядка і стовпця контрольні символи перевірки на парність (табл. 3.1).

Таблиця 3.1

m1 m2 m3 m1+m2+m3

m4 m5 m6 m4+m5+m6

m7 m8 m9 m7+m8+m9

m1+m4+m7 m2+m5+m8 m3+m6+m9 m1+m2+...+m9

Якщо у процесі передачі в цій таблиці виникне одна помилка, то перевірка на парність у відповідному рядку і стовпці не виконуватиметься. Координати помилки однозначно визначаються номерами стовпця і рядка, в яких не виконується перевірка на парність. Відтак, такий код може не тільки виявляти, але й виправляти помилки.

Описаний метод кодування називається ітеративним. Його застосування доцільне, якщо дані формуються у вигляді масивів, наприклад, в шинах ЕОМ, в пам'яті, що має табличну структуру.

Недоліком такого кодування є значна надлишковість при порівняно низькій виправній здатності.

Мікропроцесорні системи