
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Математическая статистика и прогнозирование
|
|
Методические указания к выполнению контрольной работы
для студентов направления 230400.62
заочной формы обучения
Одобрено
редакционно-издательским советом
Балаковского института техники,
технологии и управления
Балаково 2013
ОСНОВНЫЕ ПОНЯТИЯ
1. Вариационные ряды
Генеральной совокупностью называется вся подлежащая изучению совокупность объектов (наблюдений).
Выборочной совокупностью, или просто выборкой, называется совокупность случайно отобранных из генеральной совокупности объектов.
Объемом совокупности (выборочной или генеральной) называется число объектов в этой совокупности. Различные наблюдаемые значения признака называют вариантами (обозначаются хi). Числа, показывающие, сколько раз встречаются варианты в совокупности, называются частотами (обозначаются ni). Тогда объем выборки можно определить как n=∑ni. Отношение частот к объему выборки wi=ni/n называют относительными частотами. Последовательность вариант, записанных в порядке возрастания или убывания с соответствующими им частотами (или относительными частотами) называется вариационным рядом. Вариационный ряд называется дискретным, если любые его варианты отличаются на постоянную величину, и непрерывным (интервальным), если его значения могут отличаться одно от другого на сколь угодно малую величину.
Для наглядности представления вариационного ряда строят различные графики статистического распределения, в частности, полигон и гистограмму. Полигон, как правило, служит для изображения дискретного вариационного ряда, и представляет собой ломаную, в которой концы отрезков имеют координаты (xi, ni) или (xi, wi). Гистограмма служит для изображения интервальных вариационных рядов и представляет собой ступенчатую фигуру из прямоугольников с основаниями, равными интервалам значений признака (x i–1, xi), и высотами, равными частотам ni (или относительным частотам wi) интервалов. Если соединить середины верхних оснований прямоугольников отрезками прямой, то можно получить полигон того же распределения.
2. Точечные и интервальные оценки параметров распределения
Статистической оценкой  неизвестного параметра θ генеральной совокупности называют функцию наблюдений над случайной величиной X:
неизвестного параметра θ генеральной совокупности называют функцию наблюдений над случайной величиной X:  . Поскольку X1, X2, …, Xn – случайные величины, то и оценка
. Поскольку X1, X2, …, Xn – случайные величины, то и оценка  также является случайной величиной, в отличие от оцениваемого параметра θ. Оценка
также является случайной величиной, в отличие от оцениваемого параметра θ. Оценка  называется несмещенной, если ее математическое ожидание равно оцениваемому параметру, т.е. М(
называется несмещенной, если ее математическое ожидание равно оцениваемому параметру, т.е. М( )=θ. В противном случае оценка называется смещенной. Несмещенная оценка
)=θ. В противном случае оценка называется смещенной. Несмещенная оценка  называется эффективной, если она имеет наименьшую дисперсию среди всех возможных несмещенных оценок параметра θ, вычисленных по выборкам одного и того же объема Оценка
называется эффективной, если она имеет наименьшую дисперсию среди всех возможных несмещенных оценок параметра θ, вычисленных по выборкам одного и того же объема Оценка  называется состоятельной, если она сходится по вероятности к оцениваемому параметру:
называется состоятельной, если она сходится по вероятности к оцениваемому параметру:
 для любого ε > 0.
для любого ε > 0.
Генеральной средней 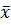 конечной генеральной совокупности называют среднее арифметическое значений признака генеральной совокупности. Пусть из генеральной совокупности объема n отобрана случайная выборка X1, X2,..., Xn. Выборочная средняя
конечной генеральной совокупности называют среднее арифметическое значений признака генеральной совокупности. Пусть из генеральной совокупности объема n отобрана случайная выборка X1, X2,..., Xn. Выборочная средняя  , которая является несмещенной и состоятельной оценкой генеральной средней, определяется по формуле:
, которая является несмещенной и состоятельной оценкой генеральной средней, определяется по формуле:
 (2.1)
(2.1)
Если значения признака x1, x2,..., xk имеют соответственно частоты n1, n 2,..., n k, причем n = ∑ ni, то
 (2.2)
(2.2)
В качестве характеристики разброса значений количественного признака X вокруг своего среднего значения используется дисперсия. В случае конечной генеральной совокупности генеральной дисперсией D = σ2 называют среднее арифметическое квадратов отклонений значений признака генеральной совокупности от их среднего значения  . Выборочной дисперсией Dв называют среднее арифметическое квадратов отклонений наблюдаемых значений признака от их среднего значения
. Выборочной дисперсией Dв называют среднее арифметическое квадратов отклонений наблюдаемых значений признака от их среднего значения  . Выборочная дисперсия является смещенной оценкой генеральной дисперсии.
. Выборочная дисперсия является смещенной оценкой генеральной дисперсии.
Если все значения x 1, x 2,..., x n признака выборки объема n различны, то
 (2.3)
(2.3)
Если значения признака x1, x2,..., xk имеют соответственно частоты n1, n 2,..., n k, причем n = ∑ ni, то
 (2.4)
(2.4)
Несмещенной оценкой генеральной дисперсии является исправленная выборочная дисперсия
 (2.5)
(2.5)
Если в качестве оценки параметра предлагается число – точка на координатной оси, то оценка называется точечной. Оценки, рассмотренные выше – точечные.
Интервальной оценкой параметра θ называют числовой интервал  , который с заданной вероятностью γ накрывает неизвестное значение параметра θ. Такой интервал называется доверительным, а вероятность γ называется доверительной вероятностью, или надежностью оценки.
, который с заданной вероятностью γ накрывает неизвестное значение параметра θ. Такой интервал называется доверительным, а вероятность γ называется доверительной вероятностью, или надежностью оценки.
Границы доверительного интервала и его длина находятся по выборочным данным, и являются случайными величинами. Величина доверительного интервала уменьшается с ростом объема выборки n и увеличивается с ростом доверительной вероятности γ. Если количественный признак генеральной совокупности X имеет нормальное распределение, то доверительный интервал для математического ожидания имеет вид

 (2.6)
(2.6)
В случае, когда генеральная дисперсия D = σ2 является известной величиной, то точность оценки δ находится по формуле
 ,, (2.7)
,, (2.7)
где число t определяется из равенства Φ(t) = γ/2, т.е. по таблице функции Лапласа (приложение 1) находят значение аргумента t, которому соответствует значение функции Лапласа γ/2.
В случае, когда генеральная дисперсия неизвестна, а известна лишь ее исправленная выборочная оценка  , то точность оценки δ находится по формуле
, то точность оценки δ находится по формуле
 , (2.8)
, (2.8)
где значение числа T(1 – γ; n –1) определяется по таблице критических точек распределения Стьюдента (приложение 2) при уровне вероятности α=1– γ и числе степеней свободы n–1.
Доверительный интервал для среднеквадратического отклонения σ нормального распределения имеет вид
 , (2.9)
, (2.9)
где значения χ12, χ22 находятся по таблице критических точек распределения χ2 (приложение 3) при числе степеней свободы n–1 и уровнях вероятности (1 + γ) /2 и (1 – γ) /2 соответственно.
3. Проверка гипотез.
Статистической гипотезой называется любое предположение о виде неизвестного распределения или о параметрах закона распределения.
Выдвинутуюгипотезу называют нулевой (основной) гипотезой Н0. Если выдвинутая гипотеза Н0 будет отвергнута, то имеет место противоречащая ей гипотеза Н1, которая называется конкурирующей (альтернативной).
Для проверки нулевой гипотезы используют специально подобранную случайную величину (статистический критерий). После выбора критерия множество всех его возможных значений разбивают на два подмножества: одно из них содержит значения критерия, при которых нулевая гипотеза отвергается (критическая область), а другое содержит те значения критерия, при которых гипотеза принимается (область принятия гипотезы). Если наблюдаемое значение критерия принадлежит критической области, то нулевую гипотезу отвергают в пользу конкурирующей гипотезы; если наблюдаемое значение критерия принадлежит области принятия гипотезы, то нулевую гипотезу принимают.
Критическими точками Ккр называют точки, отделяющие критическую область от области принятия гипотезы.
Рассмотрим способы проверки некоторых наиболее часто встречающихся гипотез.
3.1. Гипотеза о равенстве генеральной средней нормальной совокупности заданному числовому значению.
Пусть генеральная совокупность Х распределена нормально, причем имеются основания предполагать, что генеральная средняя этой совокупности 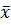 равна некоторому значению а.
равна некоторому значению а.
Предполагаем, что дисперсия генеральной совокупности D = σ2 известна (например, может быть найдена теоретически, или вычислена по выборке большого объема). Кроме того, по произведенной выборке объема n найдена выборочная средняя  . Требуется по выборочной средней при заданном уровне значимости α проверить нулевую гипотезу Н0:
. Требуется по выборочной средней при заданном уровне значимости α проверить нулевую гипотезу Н0: 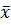 = а. Для этого необходимо вычислить наблюдаемое значение критерия
= а. Для этого необходимо вычислить наблюдаемое значение критерия
 . (3.1)
. (3.1)
1) При конкурирующей гипотезе Н1: 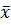 ≠ а критическую точку Uкр находим по таблице функции Лапласа (приложение 1) из условия Φ(Uкр) = (1 – α)/2. Если |Uнабл| < Uкр, то принимается нулевая гипотеза. В противном случае нулевую гипотезу отвергают.
≠ а критическую точку Uкр находим по таблице функции Лапласа (приложение 1) из условия Φ(Uкр) = (1 – α)/2. Если |Uнабл| < Uкр, то принимается нулевая гипотеза. В противном случае нулевую гипотезу отвергают.
2) При конкурирующей гипотезе Н1: 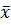 > а критическую точку Uкр находим по таблице функции Лапласа из условия Φ(U кр) = (1 – 2α) /2. Если Uнабл < Uкр, то принимается нулевая гипотеза. В противном случае нулевую гипотезу отвергают.
> а критическую точку Uкр находим по таблице функции Лапласа из условия Φ(U кр) = (1 – 2α) /2. Если Uнабл < Uкр, то принимается нулевая гипотеза. В противном случае нулевую гипотезу отвергают.
3) При конкурирующей гипотезе Н1: 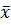 < а критическую точку Uкр находим по таблице функции Лапласа из условия Φ(Uкр) = (1 – 2α)/2. Нулевая гипотеза принимается, если Uнабл > –Uкр. В противном случае нулевую гипотезу отвергают.
< а критическую точку Uкр находим по таблице функции Лапласа из условия Φ(Uкр) = (1 – 2α)/2. Нулевая гипотеза принимается, если Uнабл > –Uкр. В противном случае нулевую гипотезу отвергают.
Предположим теперь, что дисперсия генеральной совокупности D = σ2 неизвестна, а известна только ее исправленная выборочная оценка  = s2. Для того, чтобы при заданном уровне значимости α проверить нулевую гипотезу Н0:
= s2. Для того, чтобы при заданном уровне значимости α проверить нулевую гипотезу Н0: 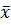 = а, нужно вычислить наблюдаемое значение критерия
= а, нужно вычислить наблюдаемое значение критерия
 (3.2)
(3.2)
1) При конкурирующей гипотезе Н1: 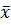 ≠ а критическую точку Tкр(α, n–1) находим по таблице критических точек распределения Стьюдента (приложение 2) при n–1 степенях свободы и вероятности α. Если |Tнабл| < Tкр, то принимается нулевая гипотеза. В противном случае нулевую гипотезу отвергают.
≠ а критическую точку Tкр(α, n–1) находим по таблице критических точек распределения Стьюдента (приложение 2) при n–1 степенях свободы и вероятности α. Если |Tнабл| < Tкр, то принимается нулевая гипотеза. В противном случае нулевую гипотезу отвергают.
2) При конкурирующей гипотезе Н1: 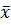 > а критическую точку Tкр (2α, n – 1 находим по таблице критических точек распределения Стьюдента при n – 1 степенях свободы и вероятности 2α. Если Tнабл < Tкр, то принимается нулевая гипотеза. В противном случае нулевую гипотезу отвергают.
> а критическую точку Tкр (2α, n – 1 находим по таблице критических точек распределения Стьюдента при n – 1 степенях свободы и вероятности 2α. Если Tнабл < Tкр, то принимается нулевая гипотеза. В противном случае нулевую гипотезу отвергают.
3) При конкурирующей гипотезе Н1: 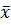 < а критическую точку Tкр(2α, n –1) находим по таблице критических точек распределения Стьюдента при n –1 степенях свободы и вероятности 2α. Если T набл > –T кр, то принимается нулевая гипотеза. В противном случае нулевую гипотезу отвергают.
< а критическую точку Tкр(2α, n –1) находим по таблице критических точек распределения Стьюдента при n –1 степенях свободы и вероятности 2α. Если T набл > –T кр, то принимается нулевая гипотеза. В противном случае нулевую гипотезу отвергают.
3.2 Гипотеза о равенстве двух средних нормальных генеральных совокупностей.
Пусть генеральные совокупности Х1 и Х2 распределены нормально, причем генеральные средние этих совокупностей  и
и  неизвестны. По произведенным выборкам объемов n1 и n2 найдены выборочные средние
неизвестны. По произведенным выборкам объемов n1 и n2 найдены выборочные средние  и
и  .
.
Предполагаем, что дисперсии обеих генеральных совокупностей известны, и равны  и
и  . Требуется при заданном уровне значимости α проверить нулевую гипотезу Н0:
. Требуется при заданном уровне значимости α проверить нулевую гипотезу Н0:  =
=  . Вычисляем наблюдаемое значение критерия
. Вычисляем наблюдаемое значение критерия
 . (3.3)
. (3.3)
1) При конкурирующей гипотезе Н1:  ≠
≠  критическую точку Uкр находим по таблице функции Лапласа из условия Φ(Uкр) = (1 – α)/2. Если |Uнабл| < Uкр, то принимается нулевая гипотеза. В противном случае нулевую гипотезу отвергают.
критическую точку Uкр находим по таблице функции Лапласа из условия Φ(Uкр) = (1 – α)/2. Если |Uнабл| < Uкр, то принимается нулевая гипотеза. В противном случае нулевую гипотезу отвергают.
2) При конкурирующей гипотезе Н1:  >
>  критическую точку Uкр находим по таблице функции Лапласа из условия Φ(Uкр) = (1 – 2α)/2. Если Uнабл < Uкр, то принимается нулевая гипотеза. В противном случае нулевую гипотезу отвергают.
критическую точку Uкр находим по таблице функции Лапласа из условия Φ(Uкр) = (1 – 2α)/2. Если Uнабл < Uкр, то принимается нулевая гипотеза. В противном случае нулевую гипотезу отвергают.
3) При конкурирующей гипотезе Н1:  <
<  критическую точку Uкр находим по таблице функции Лапласа из условия Φ(Uкр) = (1 – 2α)/2. Если Uнабл > –U кр, то принимается нулевая гипотеза. В противном случае нулевую гипотезу отвергают.
критическую точку Uкр находим по таблице функции Лапласа из условия Φ(Uкр) = (1 – 2α)/2. Если Uнабл > –U кр, то принимается нулевая гипотеза. В противном случае нулевую гипотезу отвергают.
Предположим теперь, что дисперсии обеих генеральных совокупностей неизвестны, а известны только их исправленные выборочные оценки  и
и  , а выборки имеют небольшой объем (меньше 30). Предполагается, что дисперсии двух генеральных совокупностей одинаковы. В этом случае нужно вычислить наблюдаемое значение критерия
, а выборки имеют небольшой объем (меньше 30). Предполагается, что дисперсии двух генеральных совокупностей одинаковы. В этом случае нужно вычислить наблюдаемое значение критерия
 (3.4)
(3.4)
1) При конкурирующей гипотезе Н1:  ≠
≠  критическую точку Tкр(α, n1+n2–2) находим по таблице критических точек распределения Стьюдента (приложение 2) при n1+n2–2 степенях свободы и вероятности α. Если |Tнабл|< Tкр, то принимается нулевая гипотеза. В противном случае нулевую гипотезу отвергают.
критическую точку Tкр(α, n1+n2–2) находим по таблице критических точек распределения Стьюдента (приложение 2) при n1+n2–2 степенях свободы и вероятности α. Если |Tнабл|< Tкр, то принимается нулевая гипотеза. В противном случае нулевую гипотезу отвергают.
2) При конкурирующей гипотезе Н1:  >
>  критическую точку Tкр(2α, n1+ n2 – 2) находим по таблице критических точек распределения Стьюдента при n1+n2–2 степенях свободы и вероятности 2α. Если Tнабл < Tкр, то принимается нулевая гипотеза. В противном случае нулевую гипотезу отвергают.
критическую точку Tкр(2α, n1+ n2 – 2) находим по таблице критических точек распределения Стьюдента при n1+n2–2 степенях свободы и вероятности 2α. Если Tнабл < Tкр, то принимается нулевая гипотеза. В противном случае нулевую гипотезу отвергают.
3) При конкурирующей гипотезе Н1:  <
<  критическую точку Tкр(2α, n1 + n2 – 2) находим по таблице критических точек распределения Стьюдента при n1+n2–2 степенях свободы и вероятности 2α. Если Tнабл > –T кр, то принимается нулевая гипотеза. В противном случае нулевую гипотезу отвергают.
критическую точку Tкр(2α, n1 + n2 – 2) находим по таблице критических точек распределения Стьюдента при n1+n2–2 степенях свободы и вероятности 2α. Если Tнабл > –T кр, то принимается нулевая гипотеза. В противном случае нулевую гипотезу отвергают.
4. Регрессионный и корреляционный анализ.
Зависимость между переменными величинами, когда каждому значению одной переменной может соответствовать множество значений другой переменной, имеющее определенное распределение, называется статистической. Статистические связи между переменными изучаются методами корреляционного и регрессионного анализа. Основной задачей регрессионного анализа является установление формы и изучение зависимости между переменными, корреляционного анализа – выявление связи между случайными переменными и оценка ее тесноты. В регрессионном анализе рассматривается зависимость случайного результативного признака y от неслучайных факторных признаков x1, x2,..., xn. В случае единственного факторного признака x различают следующие виды регрессий: линейную, гиперболическую, показательную, степенную, логарифмическую, параболическую и т.д. Предположим, что для оценки параметров регрессии взята выборка, содержащая n пар значений (xi, yi), где i = 1, 2, …, n. Оценкой предложенных выше уравнений регрессии являются выборочные уравнения регрессии:
- линейное  ;
;
- гиперболическое  ;
;
- показательное 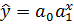 ;
;
- степенное 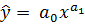 ;
;
- логарифмическое  ;
;
- параболическое 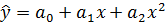 ,
,
где параметры a0, a1, a2 являются точечными оценками соответствующих параметров исходного уравнения и могут быть найдены на основе метода наименьших квадратов.
Сущность метода наименьших квадратов заключается в нахождении параметров модели a0, a1, при которых минимизируется сумма квадратов отклонений эмпирических (фактических) значений результативного признака от теоретических, полученных по выборочному уравнению регрессии
 .
.
Для нахождения параметров a0, a1 линейного уравнения регрессии  решается система уравнений
решается система уравнений
 (4.1)
(4.1)
Для параболического уравнения регрессии 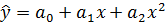 система уравнений для нахождения параметров a0, a1, a2 имеет вид
система уравнений для нахождения параметров a0, a1, a2 имеет вид
 (4.2)
(4.2)
Все предложенные выше виды нелинейных регрессий (кроме параболической) могут быть сведены к линейной путем какой-либо замены переменной. Для гиперболической регрессии вводится переменная x′= 1/x, для логарифмической регрессии x′= lnx, уравнения показательной и степенной регрессии предварительно логарифмируют.
Регрессионную модель удобно представлять графически. Для этого на координатной плоскости откладываются точки Pi (xi, yi), (i = 1, 2, …, n) (рис. 4.1). Полученный график называется диаграммой рассеивания.

Рис. 4.1. Диаграмма рассеивания
Построив диаграмму рассеяния, можно подобрать вид уравнения регрессии. На рис. 4.1 для одних и тех же экспериментальных точек построены линейная и показательная регрессии. Видим, что экспериментальные точки располагаются ближе к линии  , чем к прямой. Следовательно, можно сделать вывод, что показательная регрессия более адекватно описывает фактические данные, чем линейная.
, чем к прямой. Следовательно, можно сделать вывод, что показательная регрессия более адекватно описывает фактические данные, чем линейная.
Однако по графику можно только приближенно сделать вывод о качестве той или иной модели. Для более точной оценки адекватности (значимости) уравнения регрессии на уровне значимости α вычисляют наблюдаемое значение случайной величины
 , (4.3)
, (4.3)
где остаточная дисперсия  и дисперсия уравнения регрессии
и дисперсия уравнения регрессии  находятся по формулам
находятся по формулам
 ,
,  (4.4)
(4.4)
Далее находим критическое значение критерия F(α, 1; n – 2) по таблице критических точек распределения Фишера (приложение 4) при k1=1, k2 = n – 2 степенях свободы и уровне значимости α. Если Fнабл > F(α; 1; n – 2), то уравнение регрессии признается значимым, в противном случае уравнение регрессии признается незначимым, т.е. статистически подтверждается отсутствие линейной связи между факторным и результативным признаком.
Рассмотрим более подробно линейное уравнение регрессии. В качестве универсального показателя тесноты связи между величинами x и y используется выборочный линейный коэффициент корреляции
 (4.5)
(4.5)
Здесь sx и sy – средние квадратические отклонения соответствующих признаков (факторного и результативного).
Линейный коэффициент корреляции изменяется в пределах –1 ≤ r ≤ 1. Если r > 0, то связь между переменными x и у прямая, если r < 0, то связь между переменными x и у обратная. При r = 0 связь между переменными отсутствует. При |r| = 1 связь между x и у функциональная, т.е. наблюдаемые значения располагаются точно на прямой.
Пусть вычисленное значение r≠ 0. Проверим гипотезу H0 об отсутствии линейной корреляционной связи между переменными, т.е. H0: ρ= 0 при альтернативной гипотезе H1: ρ ≠ 0. Для проверки этой гипотезы на уровне значимости α вычисляют наблюдаемое значение критерия
 . (4.6)
. (4.6)
Критическое значение критерия T(1–α, n–2) находят по таблице критических точек распределения Стьюдента (приложение 2) для числа степеней свободы n – 2 и уровня значимости α. Если Tнабл < T(α, n – 2), то гипотеза H0 принимается, в противном случае гипотеза H0 отвергается, т.е. коэффициент корреляции признается существенно отличающимся от нуля.
По уравнению линейной регрессии можно получить точечный и интервальный прогнозы.
Точечный прогноз заключается в получении прогнозного значения уp, которое определяется путем подстановки в уравнение регрессии  соответствующего (прогнозного) значения xp
соответствующего (прогнозного) значения xp
 .
.
Интервальный прогноз заключается в построении доверительного интервала прогноза, т. е. нижней и верхней границ уpmin, уpmax интервала, содержащего точную величину для прогнозного значения  . Доверительный интервал всегда определяется с заданной вероятностью (степенью уверенности), соответствующей принятому значению уровня значимости α. Предварительно вычисляется стандартная ошибка прогноза
. Доверительный интервал всегда определяется с заданной вероятностью (степенью уверенности), соответствующей принятому значению уровня значимости α. Предварительно вычисляется стандартная ошибка прогноза 
 (4.7)
(4.7)
где 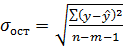 ,
,
затем строится доверительный интервал прогноза, т. е. определяются нижняя  и верхняя
и верхняя  границы интервала прогноза
границы интервала прогноза
 ,
,
где  , значение t находят по таблице критических точек распределения Стьюдента для числа степеней свободы n–2 и уровня значимости α.
, значение t находят по таблице критических точек распределения Стьюдента для числа степеней свободы n–2 и уровня значимости α.
5. Моделирование временных рядов и прогнозирование
Временным рядом (рядом динамики, динамическим рядом) называется упорядоченная во времени последовательность численных показателей{(yi,ti), i=1,2,...,n}, характеризующих уровни развития изучаемого явления в последовательные моменты или периоды времени.
Величины yi называются уровнями ряда, а ti – временными метками (моменты или интервалы наблюдения). Обычно рассматриваются временные ряды с равными интервалами между наблюдениями, в качестве значений ti берутся порядковые номера наблюдений и временной ряд представляется в виде последовательности  , где n – количество наблюдений.
, где n – количество наблюдений.
Целью исследования временного ряда является выявление закономерностей в изменении уровней ряда и построении его модели в целях прогнозирования и исследования взаимосвязей между явлениями.
Моделирование тенденции временного ряда начинается с проверки наличия тенденции. Для этого наиболее широко применяются метод сравнения средних и метод Фостера-Стюарта.
Для получения ряда с меньшим разбросом уровней, что в ряде случаев позволяет на основе визуального анализа сделать вывод о наличии тенденции, применяется сглаживание временного ряда.
Сглаживание временного ряда по методу скользящей средней заключается в замене исходных уровней ряда yt сглаженными значениями y′t, которые получаются как среднее значение определенного числа уровней исходного ряда, симметрично окружающих значение yt. В результате получается временной ряд y′t, меньше подверженный колебаниям.
Для вычисления сглаженных значений y′t по методу простой скользящей средней используются следующие формулы:
1) Нечетный интервал сглаживания g = 2p+1 (интервал сглаживания – количество исходных уровней ряда (yt), используемых для сглаживания):
 (5.5)
(5.5)
где уt – фактическое значение уровня исходного ряда в момент t; y′t – значение скользящей средней в момент t; 2р+1- длина интервала сглаживания. Формула (5.5) при интервалах сглаживания g = 3 и g = 5 принимает вид

2) Четный интервал сглаживания g = 2p:
 (5.6)
(5.6)
Формула (5.6) при интервалах сглаживания g = 2 и g = 4 принимает вид

При использовании скользящей средней с длиной активного участка g = 2p+1 первые и последние р уровней ряда сгладить нельзя, их значения теряются. Для восстановления потерянных значений временного ряда можно использовать следующий прием:
а) Вычисляется средний прирост ∆у на последнем активном участке 

где g – длина активного участка.
б) Определяются значения последних р=(g–1)/2 уровней сглаженного временного ряда с помощью последовательного прибавления среднего абсолютного прироста ∆у к последнему сглаженному значению y′n–p

Аналогичная процедура применяется для восстановления первых р уровней временного ряда.
Аналитическим выравниванием временного ряда называют нахождение аналитической функции ŷ = f(t), характеризующей основную тенденцию изменения уровней ряда с течением времени. Сама функция f(t) носит название кривой роста.
Чаще всего в качестве кривой роста применяются следующие функции:
- линейная  ; (5.7)
; (5.7)
- парабола второго и более высоких порядков
- 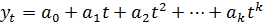 ; (5.9)
; (5.9)
- гиперболическая  ; (5.10)
; (5.10)
- экспонента 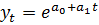 ; (5.11)
; (5.11)
- показательная  ; (5.12)
; (5.12)
- степенная  . (5.13)
. (5.13)
Построение таких функций аналогично построению уравнений парной регрессии (линейной или нелинейной) с учетом того, что в качестве зависимой переменной используются фактические уровни временного ряда yt, а в качестве независимой переменной моменты времени t = 1,2,..., n.
СОДЕРЖАНИЕ КОНТРОЛЬНОЙ РАБОТЫ
Контрольная работа состоит из трех заданий, выполняемых по индивидуальному варианту. Во всех заданиях значение N1-последняя цифра зачетной книжки, N2-предпоследняя цифра зачетной книжки.
Задача 1.
Размер обработанных на некотором станке деталей может быть рассмотрен как случайная величина Х, распределенная по нормальному закону. Для контроля качества деталей было произведено 50 измерений. Результаты измерений приведены в табл. 1
1) Провести группировку данных, разбив варианты на 8 интервалов.
2) Для сгруппированного ряда построить гистограмму частот.
3) Найти выборочную среднюю, выборочную дисперсию, исправленную выборочную дисперсию, исправленное выборочное среднеквадратическое отклонение случайной величины Х.
4) Построить доверительный интервал для генеральной средней и генерального среднеквадратического отклонения с заданным уровнем доверительной вероятности γ=0,95.
5) Проектный размер детали должен быть равен а (табл. 2). При уровне значимости α=0,05 проверить утверждение производителя о совпадении размера произведенных деталей с проектным размером.
Таблица1
| N1 | ||||||||||
| i | xi | |||||||||
| 6,42+N2 | 3,23+N2 | 4,43+N2 | 4,04+N2 | 4,20+N2 | 1,38+N2 | 4,25+N2 | 0,94+N2 | 3,14+N2 | 6,63+N2 | |
| 2,74+N2 | 2,05+N2 | 2,27+N2 | 2,71+N2 | 4,31+N2 | 0,73+N2 | 2,27+N2 | 3,57+N2 | 2,44+N2 | 5,16+N2 | |
| 9,28+N2 | 4,56+N2 | 3,18+N2 | 2,88+N2 | 4,39+N2 | 0,36+N2 | 3,86+N2 | 2,69+N2 | 4,13+N2 | 8,22+N2 | |
| 6,66+N2 | 2,50+N2 | 5,84+N2 | 3,42+N2 | 4,58+N2 | 6,59+N2 | 2,44+N2 | 1,78+N2 | 1,83+N2 | 7,66+N2 | |
| 4,66+N2 | 2,54+N2 | 3,38+N2 | 6,31+N2 | 4,67+N2 | 4,43+N2 | 2,64+N2 | 0,72+N2 | 1,63+N2 | 2,47+N2 | |
| 1,41+N2 | 3,18+N2 | 4,62+N2 | 4,12+N2 | 5,92+N2 | 1,68+N2 | 3,64+N2 | 2,06+N2 | 2,92+N2 | 10,99+N2 | |
| 10,86+N2 | 2,78+N2 | 3,87+N2 | 3,81+N2 | 4,98+N2 | 0,79+N2 | 2,72+N2 | 2,95+N2 | 3,63+N2 | 7,36+N2 | |
| 7,79+N2 | 2,83+N2 | 4,09+N2 | 3,82+N2 | 5,34+N2 | 1,02+N2 | 3,16+N2 | 5,12+N2 | 1,09+N2 | 9,48+N2 | |
| 5,47+N2 | 2,98+N2 | 9,62+N2 | 3,94+N2 | 5,38+N2 | 1,14+N2 | 3,19+N2 | 0,73+N2 | 4,27+N2 | 6,75+N2 | |
| 6,33+N2 | 3,07+N2 | 2,21+N2 | 3,96+N2 | 5,68+N2 | 1,30+N2 | 3,25+N2 | 8,20+N2 | 3,16+N2 | 4,70+N2 | |
| 6,42+N2 | 3,07+N2 | 4,55+N2 | 1,78+N2 | 5,84+N2 | 1,43+N2 | 3,26+N2 | 5,75+N2 | 2,84+N2 | 9,01+N2 | |
| 11,45+N2 | 2,71+N2 | 3,55+N2 | 3,78+N2 | 4,72+N2 | 0,46+N2 | 2,66+N2 | 8,27+N2 | 1,77+N2 | 6,40+N2 | |
| 6,55+N2 | 1,94+N2 | 4,73+N2 | 4,12+N2 | 5,94+N2 | 1,74+N2 | 4,76+N2 | 8,26+N2 | 1,48+N2 | 9,64+N2 | |
| 8,52+N2 | 3,26+N2 | 5,07+N2 | 4,25+N2 | 6,12+N2 | 2,15+N2 | 3,51+N2 | 4,65+N2 | 3,03+N2 | 10,10+N2 | |
| 6,64+N2 | 3,40+N2 | 8,33+N2 | 4,28+N2 | 6,36+N2 | 4,90+N2 | 2,23+N2 | 2,91+N2 | 1,89+N2 | 2,47+N2 | |
| 4,24+N2 | 3,49+N2 | 5,32+N2 | 4,31+N2 | 6,37+N2 | 2,58+N2 | 4,51+N2 | 4,17+N2 | 2,42+N2 | 6,13+N2 | |
| 6,86+N2 | 3,49+N2 | 5,35+N2 | 4,36+N2 | 6,98+N2 | 2,74+N2 | 3,78+N2 | 7,56+N2 | 3,62+N2 | 9,60+N2 | |
| 7,95+N2 | 3,51+N2 | 6,33+N2 | 4,48+N2 | 7,25+N2 | 3,05+N2 | 4,08+N2 | 3,29+N2 | 1,39+N2 | 10,03+N2 | |
| 6,98+N2 | 3,51+N2 | 7,32+N2 | 6,75+N2 | 7,52+N2 | 3,13+N2 | 4,54+N2 | 7,23+N2 | 3,69+N2 | 10,22+N2 | |
| 7,48+N2 | 3,62+N2 | 5,64+N2 | 4,87+N2 | 7,56+N2 | 3,13+N2 | 3,37+N2 | 7,43+N2 | 1,88+N2 | 11,26+N2 | |
| 7,69+N2 | 3,70+N2 | 5,64+N2 | 4,91+N2 | 7,56+N2 | 3,17+N2 | 4,19+N2 | 4,86+N2 | 2,94+N2 | 7,72+N2 | |
| 7,74+N2 | 3,82+N2 | 5,73+N2 | 5,03+N2 | 8,02+N2 | 3,20+N2 | 5,14+N2 | 8,70+N2 | 1,96+N2 | 5,79+N2 | |
| 5,24+N2 | 5,82+N2 | 7,24+N2 | 6,68+N2 | 8,21+N2 | 3,25+N2 | 3,35+N2 | 7,67+N2 | 2,39+N2 | 8,60+N2 | |
| 7,84+N2 | 3,84+N2 | 5,92+N2 | 6,72+N2 | 8,54+N2 | 3,34+N2 | 4,07+N2 | 3,75+N2 | 3,92+N2 | 9,10+N2 | |
| 6,91+N2 | 3,87+N2 | 5,94+N2 | 5,31+N2 | 8,65+N2 | 3,57+N2 | 3,70+N2 | 5,06+N2 | 2,58+N2 | 5,70+N2 | |
| 7,97+N2 | 3,89+N2 | 5,99+N2 | 5,34+N2 | 8,69+N2 | 3,61+N2 | 4,27+N2 | 9,00+N2 | 3,52+N2 | 9,03+N2 | |
| 8,44+N2 | 4,02+N2 | 6,02+N2 | 5,45+N2 | 8,84+N2 | 3,80+N2 | 4,50+N2 | 5,57+N2 | 2,99+N2 | 7,61+N2 | |
| 6,64+N2 | 4,21+N2 | 6,15+N2 | 5,49+N2 | 8,97+N2 | 3,85+N2 | 4,12+N2 | 6,06+N2 | 3,48+N2 | 8,64+N2 | |
| 8,58+N2 | 4,24+N2 | 6,20+N2 | 5,58+N2 | 9,01+N2 | 3,94+N2 | 3,40+N2 | 5,75+N2 | 2,89+N2 | 7,16+N2 | |
| 9,09+N2 | 4,33+N2 | 6,28+N2 | 5,58+N2 | 9,12+N2 | 4,18+N2 | 5,00+N2 | 5,89+N2 | 3,84+N2 | 8,09+N2 | |
| 3,77+N2 | 4,43+N2 | 5,53+N2 | 5,64+N2 | 9,25+N2 | 4,25+N2 | 3,91+N2 | 4,83+N2 | 3,26+N2 | 6,47+N2 | |
| 9,63+N2 | 4,55+N2 | 6,50+N2 | 5,62+N2 | 9,26+N2 | 0,20+N2 | 4,03+N2 | 3,89+N2 | 2,75+N2 | 8,17+N2 | |
| 9,96+N2 | 2,09+N2 | 6,59+N2 | 6,76+N2 | 9,48+N2 | 4,45+N2 | 2,44+N2 | 6,50+N2 | 3,21+N2 | 6,54+N2 | |
| 13,55+N2 | 4,60+N2 | 10,59+N2 | 5,84+N2 | 9,56+N2 | 4,56+N2 | 5,58+N2 | 5,76+N2 | 2,30+N2 | 7,09+N2 | |
| 10,51+N2 | 4,75+N2 | 6,79+N2 | 5,92+N2 | 9,61+N2 | 2,49+N2 | 4,00+N2 | 6,04+N2 | 4,88+N2 | 5,48+N2 | |
| 10,80+N2 | 4,80+N2 | 6,82+N2 | 5,94+N2 | 9,68+N2 | 6,30+N2 | 3,40+N2 | 3,95+N2 | 3,40+N2 | 8+N2 | |
| 13,46+N2 | 4,82+N2 | 3,35+N2 | 6,02+N2 | 9,84+N2 | 4,92+N2 | 5,33+N2 | 5,92+N2 | 2,54+N2 | 7,23+N2 | |
| 11,02+N2 | 4,84+N2 | 5,47+N2 | 6,18+N2 | 9,87+N2 | 5,04+N2 | 5,89+N2 | 6,72+N2 | 5,69+N2 | 9,38+N2 | |
| 16,92+N2 | 4,84+N2 | 7,69+N2 | 6,24+N2 | 9,92+N2 | 5,34+N2 | 4,49+N2 | 7,17+N2 | 2,28+N2 | 12,34+N2 | |
| 11,34+N2 | 4,88+N2 | 7,69+N2 | 6,29+N2 | 9,94+N2 | 8,74+N2 | 3,77+N2 | 6,05+N2 | 3,29+N2 | 7,91+N2 | |
| 4,91+N2 | 4,91+N2 | 7,76+N2 | 3,61+N2 | 9,97+N2 | 6,13+N2 | 4,16+N2 | 5,80+N2 | 2,61+N2 | 6,31+N2 | |
| 11,71+N2 | 5,02+N2 | 8,13+N2 | 6,38+N2 | 10,07+N2 | 6,21+N2 | 4,94+N2 | 7,15+N2 | 2,40+N2 | 7,34+N2 | |
| 11,83+N2 | 5,10+N2 | 8,21+N2 | 6,54+N2 | 10,16+N2 | 6,24+N2 | 4,34+N2 | 6,22+N2 | 3,56+N2 | 9,34+N2 | |
| 11,89+N2 | 5,29+N2 | 5,31+N2 | 5,15+N2 | 10,17+N2 | 4,61+N2 | 3,40+N2 | 5,92+N2 | 4,16+N2 | 7,81+N2 | |
| 12,91+N2 | 5,37+N2 | 8,88+N2 | 6,68+N2 | 10,25+N2 | 6.40+N2 | 5,61+N2 | 4,17+N2 | 2,41+N2 | 6,63+N2 | |
| 4,99+N2 | 5,42+N2 | 4,27+N2 | 6,72+N2 | 10,28+N2 | 0,17+N2 | 4,25+N2 | 7,02+N2 | 3,81+N2 | 9,06+N2 | |
| 13,54+N2 | 5,42+N2 | 10,68+N2 | 5,27+N2 | 10,28+N2 | 6,71+N2 | 4,78+N2 | 5,76+N2 | 2,51+N2 | 7,43+N2 | |
| 10,37+N2 | 5,49+N2 | 9,73+N2 | 6,74+N2 | 11,24+N2 | 7,87+N2 | 6,06+N2 | 7,20+N2 | 2,37+N2 | 9,14+N2 | |
| 15,92+N2 | 5,62+N2 | 6,67+N2 | 4,62+N2 | 11,32+N2 | 8,19+N2 | 4,35+N2 | 4,06+N2 | 3,32+N2 | 9,39+N2 | |
| 11,21+N2 | 3,83+N2 | 9,67+N2 | 5,73+N2 | 11,34+N2 | 5,57+N2 | 3,75+N2 | 3,92+N2 | 2,06+N2 | 7,73+N2 |
Таблица 2
| N | ||||||||||
| a | 10+N2 | 4+N2 | 6+N2 | 8+N2 | 8+N2 | 4+N2 | 4+N2 | 8+N2 | 3+N2 | 9+N2 |
Задача 2
Была исследована зависимость случайной величины Y от величины Х. В результате 10 испытаний были получены следующие результаты (табл. 3). По этим данным:
1) Построить диаграмму рассеяния.
2) Построить линейное уравнение регрессии.
3) Построить показательное уравнение регрессии.
4) Для построенных моделей проверить адекватность по F-критерию.
5) По модели с наименьшей остаточной дисперсией вычислить прогнозируемое значение y* при заданном значении x* (табл. 4).
6) Вычислить выборочный линейный коэффициент корреляции.
7) При уровне значимости α=0,05 проверить значимость коэффициента корреляции.
Таблица 3
| N1 | i | ||||||||||
| xi | 2,41 | 5,72 | 6,46 | 7,21 | 7,62 | 7,93 | 8,13 | 8,39 | 10,45 | 11,83 | |
| yi | 69,07 | 94,81 | 97,66 | 99,93 | 99,50 | 99,94 | 99,75 | 99,84 | 93,98 | 85,01 | |
| xi | 2,08 | 3,28 | 3,28 | 3,50 | 4,06 | 4,70 | 4,85 | 4,99 | 5,09 | 5,88 | |
| yi | 51,63 | 59,62 | 58,77 | 59,31 | 59,31 | 59,60 | 58,18 | 58,01 | 58,43 | 52,80 | |
| xi | 2,69 | 3,12 | 3,88 | 5,94 | 6,79 | 6,89 | 7,19 | 7,37 | 7,39 | 12,00 | |
| yi | 28,35 | 33,78 | 40,44 | 50,14 | 48,72 | 48,04 | 47,48 | 46,03 | 44,70 | 41,21 | |
| xi | 3,07 | 3,48 | 4,46 | 5,20 | 5,20 | 5,40 | 6,40 | 7,40 | 7,53 | 10,35 | |
| yi | 63,99 | 65,59 | 66,49 | 71,77 | 67,27 | 68,67 | 67,74 | 58,16 | 58,68 | 60,99 | |
| xi | 5,24 | 5,32 | 6,46 | 6,49 | 6,79 | 6,83 | 7,22 | 7,86 | 11,12 | 11,77 | |
| yi | 37,76 | 40,84 | 44,86 | 43,61 | 43,05 | 42,46 | 45,45 | 45,03 | 54,10 | 52,85 | |
| xi | 2,27 | 2,43 | 2,78 | 3,57 | 3,63 | 3,73 | 4,31 | 4,55 | 5,88 | 6,22 | |
| yi | 73,23 | 80,45 | 77,35 | 82,86 | 88,74 | 83,85 | 82,69 | 80,94 | 75,10 | 75,73 | |
| xi | 2,47 | 3,85 | 4,34 | 4,35 | 4,47 | 4,59 | 4,79 | 5,16 | 5,42 | 5,88 | |
| yi | 12,78 | 15,73 | 20,87 | 19,90 | 22,00 | 20,80 | 22,78 | 20,73 | 19,45 | 20,99 | |
| xi | 4,44 | 4,94 | 5,97 | 6,28 | 6,31 | 6,94 | 7,40 | 7,40 | 8,50 | 9,17 | |
| yi | 8,43 | 8,50 | 8,39 | 8,34 | 8,24 | 8,16 | 8,32 | 8,39 | 8,23 | 8,19 | |
| xi | 1,07 | 1,08 | 1,72 | 1,83 | 1,83 | 1,86 | 1,88 | 2,52 | 2,53 | 2,69 | |
| yi | 6,33 | 6,18 | 6,03 | 8,07 | 7,52 | 7,69 | 6,08 | 6,90 | 6,12 | 7,63 | |
| xi | 2,49 | 3,28 | 4,49 | 4,73 | 5,18 | 6,30 | 6,62 | 6,83 | 6,90 | 7,89 | |
| yi | 21,48 | 19,28 | 24,22 | 20,32 | 29,14 | 24,64 | 28,03 | 26,91 | 26,26 | 28,68 |
Таблица 4
| N1 | ||||||||||
| x* |
Задача 3.
На основе приведенных в таблице 5 данных о производстве продукции (в млн. руб.):
1. Проведите сглаживание уровней ряда с помощью трехчленной скользящей средней.
2. Проведите аналитическое выравнивание и выразите общую тенденцию роста каждого вида продукции соответствующими математическими уровнями, определите выровненные уровни ряда динамики и нанесите их на график с фактическими данными.
3. По построенному тренду сделайте прогноз по выпуску продукции на 2013 год.
Таблица5
| N1 | годы | |||||||||
| 1036,3 | 1062,2 | 1072,4 | 1127,6 | 1151,1 | 1148,3 | 1152,5 | 1134,5 | 1191,7 | 1233,0 | |
| 126,6 | 130,8 | 135,7 | 140,1 | 120,7 | 160,6 | 171,7 | 172,5 | 180,6 | 184,0 | |
| 1736,3 | 2762,2 | 3772,6 | 1827,6 | 2851,1 | 3848,3 | 1853,5 | 2834,5 | 3891,7 | 1933,0 | |
| 290,4 | 342,2 | 291,1 | 254,7 | 321,3 | 356,5 | 287,4 | 320,2 | 310,8 | 386,4 | |
| 115,2 | 126,7 | 157,5 | 188,3 | 222,4 | 178,2 | 215,6 | 258,0 | 201,7 | 147,6 | |
| 100,1 | 108,5 | 119,6 | 128,7 | 135,0 | 141,7 | 102,3 | 135,2 | 142,4 | 134,8 | |
| 290,8 | 380,5 | 430,4 | 510,2 | 498,2 | 407,2 | 398,4 | 420,6 | 485,2 | 506,3 | |
| 133,2 | 148,4 | 160,6 | 172,0 | 198,2 | 230,5 | 205,6 | 184,2 | 196,6 | 210,8 | |
| 100,5 | 122,6 | 134,0 | 142,4 | 155,8 | 161,4 | 195,2 | 140,8 | 185,5 | 164,2 | |
| 120,4 | 218,3 | 322,4 | 380,9 | 450,4 | 424,3 | 398,5 | 436,2 | 441,0 | 402,8 |
ТЕХНОЛОГИЯ ВЫПОЛНЕНИЯ КОНТРОЛЬНОЙ РАБОТЫ
Задача 1.
Некоторый технологический процесс характеризуется выходным параметром, который может быть рассмотрен как случайная величина Х. Было проведено 50 измерений этого параметра (табл. 6).
1) Провести группировку данных, разбив варианты на 8 интервалов.
2) Для сгруппированного ряда построить гистограмму частот.
3) Найти выборочную среднюю, выборочную дисперсию, исправленную выборочную дисперсию, исправленное выборочное среднеквадратическое отклонение случайной величины Х.
4) Построить доверительный интервал для генеральной средней и генерального среднеквадратического отклонения с заданным уровнем доверительной вероятности γ = 0,95.
5) При уровне значимости α = 0,05 проверить утверждение, что среднее значение величины Х соответствует проектному значению a = 25.
Таблица 6
| i | xi | i | xi | i | xi | i | xi | i | xi |
| 19,71 | 23,21 | 24,33 | 25,58 | 26,93 | |||||
| 19,83 | 23,26 | 24,36 | 25,59 | 27,18 | |||||
| 20,6 5 | 23,43 | 24,49 | 25,68 | 27,52 | |||||
| 21,1 4 | 23,49 | 24,78 | 25,75 | 28,13 | |||||
| 21,1 8 | 23,59 | 24,78 | 26,42 | 28,23 | |||||
| 21,3 3 | 23,73 | 25,08 | 26,43 | 28,51 | |||||
| 22,2 8 | 23,8 | 25,09 | 26,49 | 29,44 | |||||
| 22,4 5 | 23,89 | 25,27 | 26,52 | 29,56 | |||||
| 22,4 8 | 24,16 | 25,52 | 26,65 | 29,61 | |||||
| 23,1 5 | 24,26 | 25,57 | 26,68 | 30,39 |
Решение
1. Проведем группировку исходных данных. Найдем разность между наибольшим и наименьшим значениями признака xmax – xmin = 30,39 – 19,71 = 10,68. Тогда длина интервала составит h = 10,68/8 = 1,335 ≈ 1,4. Выберем границы интервалов (табл. 7).
Таблица 7
| i | Интервал | Середина интервала xi | Частота ni | Относительная частота wi= ni/n |
| 19,7-21,1 | 20,4 | 0,06 | ||
| 21,1-22,5 | 21,8 | 0,12 | ||
| 22,5-23, 9 | 23,2 | 0,18 | ||
| 23,9-25,3 | 24,6 | 0, 2 | ||
| 25,3-26,7 | 0,24 | |||
| 26,7-28,1 | 27,4 | 0,06 | ||
| 28,1-29,5 | 28,8 | 0,08 | ||
| 29,5-30, 9 | 30,2 | 0,06 | ||
| Σ |
2. Построим для сгруппированного ряда гистограмму частот.

3. Найдем выборочную среднюю  по формуле (2.2)
по формуле (2.2)



Найдем выборочную дисперсию Dв по формуле (2.4)


Найдем исправленную выборочную дисперсию по формуле (2.5)
 .
.
Найдем исправленное выборочное среднеквадратическое отклонение случайной величины Х

4. Построим доверительный интервал для генеральной средней с уровнем доверительной вероятности γ = 0,95. Так как значение генеральной дисперсии неизвестно, пользуемся формулой (2.10). Найдем значение t1–γ,n–1 = t0,05;49 по таблице критических точек распределения Стьюдента (приложение 2) при уровне вероятности α = 0,05 и числе степеней свободы k = n – 1 = 49. Получаем t0,05;49 = 2,01. Далее находим точность оценки
 .
.
Согласно (2.8), доверительный интервал для генеральной средней имеет вид 
 . Подставляя значения, получаем, что с вероятностью 0,95 выполнено
. Подставляя значения, получаем, что с вероятностью 0,95 выполнено  .
.
Построим доверительный интервал для генерального среднеквадратического отклонения с заданным уровнем доверительной вероятности γ = 0,95. Найдем значение  по таблице критических точек распределения χ2 (приложение 3) при уровне вероятности (1 + γ)/ 2 = 0,975 и числе степеней свободы k = n – 1 = 49. Получаем
по таблице критических точек распределения χ2 (приложение 3) при уровне вероятности (1 + γ)/ 2 = 0,975 и числе степеней свободы k = n – 1 = 49. Получаем  = 31,55, следовательно,
= 31,55, следовательно,  =5,62. Найдем значение
=5,62. Найдем значение  по таблице критических точек рас- пределения χ2 при уровне вероятности (1 – γ)/2 = 0,025 и числе степеней свободы k = n – 1 = 49. Получаем
по таблице критических точек рас- пределения χ2 при уровне вероятности (1 – γ)/2 = 0,025 и числе степеней свободы k = n – 1 = 49. Получаем  = 70,22, следовательно,
= 70,22, следовательно,  = 8,38. Согласно (2.11), доверительный интервал для генерального среднеквадратического отклонения имеет вид
= 8,38. Согласно (2.11), доверительный интервал для генерального среднеквадратического отклонения имеет вид

Подставляя значения, получаем, что с вероятностью 0,95 выполнено

или 
5. При уровне значимости α = 0,05 проверим утверждение, что среднее значение величины Х соответствует проектному значению a = 25. Так как выборка имеет большой объем (n = 50 > 30), то для проверки нулевой гипотезы Н 0: x = а в качестве критерия проверки можно принять случайную величину U, определенную по формуле (3.1). При этом в качестве генерального среднеквадратического отклонения σ можно принять выборочное значение s.
Вычислим наблюдаемое значение критерия
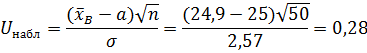
Конкурирующей является гипотеза Н 1: x ≠ а, поэтому критическую точку U кр находим по таблице функции Лапласа (приложение 1) из условия Φ(U кр) = (1 – α)/2 = 0,475. Получаем U кр=1,96. Так как | U набл| < U кр, то нет оснований отвергнуть нулевую гипотезу. Следовательно, утверждение, что среднее значение выходного параметра Х соответствует проектному значению, является статистически обоснованным.
Задача 2
Была исследована зависимость случайной величины
Date: 2016-08-30; view: 565; Нарушение авторских прав