Применение команд обработки данных к векторам и матрицам

Команда max(V) выдает значение максимального по значению элемента вектора V. Аналогично, команда min(V) извлекает минимальный элемент вектора V.

Команды mean(V) и std(V) выдают, соответственно, среднее значение и среднеквадратическое отклонение вектора V.

Команда сортировки sort(V) формирует вектор, элементы которого распределены в порядке возрастания их значений.

Команда sum(V) возвращает сумму элементов вектора V.

Команда prod(V) выдает произведение всех элементов вектора V.

Команда cumsum(V) формирует вектор того же типа и размера, любой элемент которого является суммой всех предыдущих элементов вектора V (вектор кумулятивной суммы).

Команда cumprod(V) создает вектор, элементы которого являются произведением всех предыдущих элементов вектора V.

Команда diff(V) выдает вектор, имеющий размер на единицу меньший, чем размер вектора V, элементами которого является разность между соседними элементами вектора V.

Применение описанных команд проиллюстрировано ниже на одном и том же векторе V:

>> V=[1.1.5.1.1.4]

V =

1.0000 0.1000 0.5000 0.1000 0.1000 0.4000

>> disp(length(V))

>> disp(max(V))

>> disp(min(V))

0.1000

>> disp(mean(V))

0.3667

>> disp(std(V))

0.3559

>> disp(sort(V))

0.1000 0.1000 0.1000 0.4000 0.5000 1.0000

>> disp(sum(V))

2.2000

>> disp(prod(V))

2.0000e-004

>> disp(cumsum(V))

1.0000 1.1000 1.6000 1.7000 1.8000 2.2000

>> disp(cumprod(V))

1.0000 0.1000 0.0500 0.0050 0.0005 0.0002

>> disp(diff(V))

-0.9000 0.4000 -0.4000 0 0.3000

Часто необходимо знать не только значение минимального или максимального элемента в массиве, но и его индекс (порядковый номер). Если указать второй выходной параметр, то можно получить дополнительную информацию о первом индексе элемента, значение которого является максимальным или минимальным:

>> [M,n]=max(V)

M =

n =

>> [M,n]=min(v)

M =

0.1000

n =

Для того, чтобы упорядочить вектор V по убыванию, также используем команду sort:

>> R=-sort(-V)

R =

1.0000 0.5000 0.4000 0.1000 0.1000 0.1000

Вызов sort с двумя выходными аргументами приводит к образованию массива индексов соответствия элементов упорядоченного и исходного массивов:

>> [R,ind]=sort(V)

R =

0.1000 0.1000 0.1000 0.4000 0.5000 1.0000

ind =

2 4 5 6 3 1

Применение команд обработки данных к некоторым последовательно расположенным элементам вектора не представляет труда. Например, произведение элементов вектора V со второго по шестой вычисляется так:

>> P=prod(V(2:6))

P =

2.0000e-004

Сумма элементов вектора V с четными индексами находится следующим образом:

>> ind=2:2:length(V);

>> s=sum(V(ind))

s =

0.6000

Если вектор V состоит из комплексных чисел, команды max(V) и min(V) выдают максимальный и минимальный по модулю элемент. Команда sort упорядочивает комплексный вектор по модулю, а компоненты с равными модулями располагаются в порядке возрастания фаз.

Команды max, min, mean, std, sort, sum, prod, cumsum, cumprod, diff могут применятся к матрицам. Если M матрица, то команда max(M) извлекает максимальный элемент каждого столбца:

>> A=[7 1 -1;3 4 -4; 2 3 4]

A =

7 1 -1

3 4 -4

2 3 4

>> m=max(A)

m =

7 4 4

Если указать два выходных параметра, то получим номера строк c максимальными элементами:

>> [m,n]=max(A)

m =

7 4 4

n =

1 2 3

Если в качестве второго входного параметра sum указать 2, то cуммирование произойдет по строкам. Например:

>> M=[1 2;3 4; 5 6]

M =

1 2

3 4

5 6

>> disp(sum(M,2))

Для вычисления суммы всех элементов матрицы требуется дважды применить sum:

>> disp(sum(sum(M)))

Пример:

Для матрицы

A =.

размера 6×6 вычислить величину

.

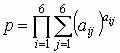Решение:

>> A=[1.5 -1 1.4 1

1 -5 -2 1 1 -2

-2.5 -1 1 -1 2

-4.3 1.2.1 -3

-2 1 1.4 1 -1

1 -2 1 1.7 1];

>> p=prod(sum(A.^A,2))

p =

2.2183e+003

Подробнее о командах обработки данных можно узнать в разделе datafun справочной системы MATLAB.

Date: 2016-08-30; view: 209; Нарушение авторских прав