
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Основные формулы для определения скоростей и ускорений точек звеньев
|
|
ЛЕКЦИЯ 3
Краткое содержание
Определение скоростей и ускорений точек звеньев при поступательном, вращательном и плоскопараллельном движениях. Планы скоростей и ускорений. Принцип подобия в планах скоростейи ускорений. Примеры кинематического исследования механизмов.
Теоретические предпосылки определения скоростей и ускорений
Основные формулы для определения скоростей и ускорений точек звеньев механизмов приведены в таблице 3.1.
Планы скоростей и ускорений
Планом скоростей (ускорений) называется диаграмма, на которой от некоторого центра (полюса) в масштабе отложены векторы скоростей (ускорений) точек тела.
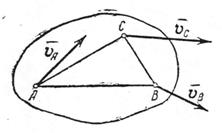
Рассмотрим тело, совершающее плоскопараллельное движение (рис.3.1).
Для плоскопараллельного движения скорости точек определяются по формулам:
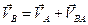 ,
,  ,
, 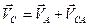 (3.1)
(3.1)
где 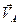 ,
, 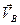 ,
, 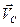 - абсолютные скорости точек А, В, С;
- абсолютные скорости точек А, В, С;
 ,
, 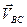 ,
,  - относительные скорости.
- относительные скорости.
План скоростей получим, если в выбранном масштабе 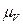 (
( ) отложим от полюса
) отложим от полюса 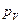 отрезки
отрезки 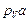 ,
,  и
и  , параллельные векторам скоростей
, параллельные векторам скоростей 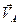
 ,
, 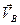 ,
, 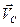 . Отрезки находятся по формулам:
. Отрезки находятся по формулам: 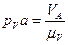 ,
, 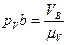 ,
, 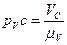 .
.

|
|
В результате построения плана скоростей получен треугольник авс (рис.3.2),который подобен треугольнику АВС. Относительных скоростей  ,
, 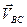 и
и  находятся по формулам:
находятся по формулам: 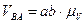
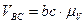 ,
, 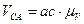 .
.
Рис.3.1 Рис.3.2
Сформулируем принцип подобия в плане скоростей:
В плане скоростей векторы относительных скоростей точек жесткого звена образуют фигуру, подобную звену, повернутую на угол 90° в сторону угловой скорости звена.
Следствие.
Пользуясь принципом подобия, достаточно на плане скоростей построить векторы скоростей только двух точек жесткого звена. Скорость же любой третьей точки определится путем построения фигуры или линии подобной данному звену.
Аналогично формулируется принцип подобия в плане ускорений.
Основные формулы для определения скоростей и ускорений точек звеньев
Таблица 3.1
| № | Вид движения | Скорость | Ускорение |
Поступательное
(ползун по стойке)
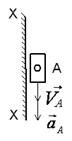
| Все точки звена имеют одинаковую скорость 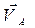 , вектор который направлен вдоль траектории движения точки A. , вектор который направлен вдоль траектории движения точки A.
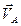 II Х-Х II Х-Х
| Все точки звена имеют одинаковые ускорения 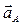 . Если вектор ускорения . Если вектор ускорения 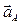 направлен в сторону направлен в сторону 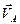 , то движение равноускоренное, если вектор ускорения , то движение равноускоренное, если вектор ускорения  направлен в противоположнyю сторону направлен в противоположнyю сторону 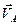 , то движение равнозамедленное. , то движение равнозамедленное.
 II Х -Хx II Х -Хx
| |
Вращательное вокруг неподвижной оси
(кривошип или коромысло относительно стойки)
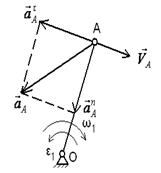
| Скорость точки А
 Вектор
Вектор 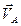 направлен перпендикулярно ОА, в сторону угловой скорости направлен перпендикулярно ОА, в сторону угловой скорости 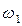 . .
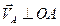
| Полное ускорение точки А
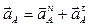 Нормальное ускорение
Нормальное ускорение  = =  Вектор
Вектор 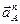 направлен по радиусу АО к центру вращения О. направлен по радиусу АО к центру вращения О.
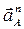 II OA.
Касательное ускорение II OA.
Касательное ускорение 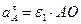 Вектор
Вектор  направлен перпендикулярно АО в сторону углового ускорения направлен перпендикулярно АО в сторону углового ускорения 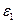
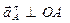
| |
Звено совершает плоскопараллельное движение
(шатун)
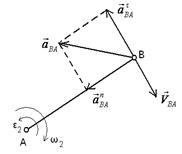
| Скорость точки В
 Относительная скорость
Относительная скорость
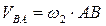 Вектор
Вектор 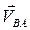 направлен перпендикулярно к ВА в сторону угловой скорости направлен перпендикулярно к ВА в сторону угловой скорости 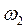 . .
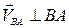
| Ускорение точки В
 Относительное ускорение
Относительное ускорение
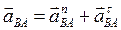 Нормальное ускорение
Нормальное ускорение
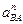 = =  Вектор
Вектор 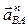 направлен параллельно АВ (от точки В к точке А) направлен параллельно АВ (от точки В к точке А)
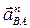 II ВА
Касательное ускорение II ВА
Касательное ускорение
 Вектор
Вектор  направлен перпендикулярно АВ направлен перпендикулярно АВ
  ВА ВА
|
Пример 3.1
Date: 2016-07-25; view: 390; Нарушение авторских прав