
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Прочностные расчеты механических систем
|
|
Прочность – это способность конструкции сопротивляться силовому воздействию без разрушения. Расчетным, количественным критерием прочности является механическое напряжение, возникающее в наиболее нагруженных точках системы. Напряжение – это сила, действующая на элементарной площадке, отнесенная к площади этой площадки. Единицы измерения напряжения – Паскаль (Па), т.е Н/м2 и Мега-Паскаль (МПа), т.е. Н/мм2.
Различают нормальное σ и касательное τ напряжения. Действующее напряжение должно быть меньше предельно допускаемого напряжения ([σ] или [ τ ]) для данного материала в данных условиях нагружения.
Для решения задачи о прочности конструкции нужно знать приложенные к ней силы и размеры соответствующих деталей. Наиболее просто найти силы, действующие на элементы статически определимой фермы.
Задание 4
Рассчитать на прочность ферму, показанную на рисунке 5, характеризующуюся параметрами, приведенными в таблице 4.

Рисунок 5 - Ферма
Таблица 4 - Варианты к заданию 4
| Переменные параметры | |||||||||
| β, град. | Последняя цифра шифра | ||||||||
| F, Н | Предпоследняя цифра шифра | ||||||||
| Постоянные параметры | |||||||||
| α =90о; L =1м; d2 =30мм; [σ] = 200 МПа (сталь) |
Для выполнения задания необходимо:
1) рассчитать силы, действующие на стержни 1 и 2. Для этого нужно рассмотреть равновесие сил (рисунок 6 а), действующих в узле (шарнире) В. В векторной форме это уравнение выглядит так: F + R1 + R2 =0, (рисунок 6 б)
в проекциях на оси X и Y:
- R1 + R2 sin (β) =0,
R2 cos (β) - F=0.
Откуда находим:
R2= F / cos ( β ),
R1= R2 sin ( β ).

а б
Рисунок 6 – Силы, действующие в узле В фермы
2) проверить выполнение условия прочности стержня 2, испытывающего сжатие (проверочный расчет) для этого:
- найти действующее напряжение по формуле:

 .
.
- сравнить его с допускаемым напряжением [σ];
- сделать вывод о выполнении условия прочности;
3) определить параметры сечения стержня 1, испытывающего растяжение (проектный расчет):
площадь сечения
S1 = π d12/4 = R1 / [σ];
откуда  .
.
Ответ привести в мм.
Задание 5
Выполнить проектный прочностной расчет консольной балки, показанной на рисунке 7, и характеризующуюся параметрами, приведенными в таблице 5, для случаев ее изготовления из (рисунок 8): а) квадратного прутка (b=h), б) прямоугольного прутка (b=2·h), в) двутавра (№), г) круглого прутка (d), д) трубы (dо= 0,8d). Сравнить массы полученных конструкций.

Рисунок 7 – Консольная балка

а) б) в) г) д) е)
Рисунок 8 – Возможные сечения консольной балки
Таблица 5 – Варианты к заданию 5
| Переменные параметры | |||||||||
| Сравнить варианты | Последняя цифра шифра | ||||||||
| а-б | а-в | а-г | а-д | б-в | б-г | б-д | в-г | в-д | г-д |
| F, Н | Предпоследняя цифра шифра | ||||||||
| Постоянные параметры | |||||||||
| L=1м; [σ] = 200 МПа (сталь); плотность стали ρ =7,8 г/мм3 |
На балку действуют внешний силовой фактор – сосредоточенная сила F (таблица 5). Наиболее «опасный» внутренний силовой фактор, возникающий в теле балки, – изгибающий момент Mu. График (эпюра) изменения Mu вдоль оси балки показан на рисунке 6. Величины моментов Mu, действующих в сечениях консольной балки, нагруженной сосредоточенной силой F, пропорциональны этой силе и расстоянию Z от точки приложения силы до соответствующего сечения (Mu = FZ). То сечение рассматриваемой балки, в котором Mu приобретает наибольшие по абсолютной величине значение («опасное» сечение) непосредственно примыкает к заделке. В нем действует изгибающий момент:
Mu мах = FL.
Изгиб вызывает искривление балки. В результате, ее слой, примыкающий к верхней поверхности, растягивается, слой у нижней поверхности сжимается, а слой, расположенный в центре («нейтральный» слой), не изменяет своей длины. Напряжения [σ], распределяются по сечению балки, пропорционально деформации соответствующих слоев (рисунок 8 е). Максимальная величина напряжений при изгибе может быть рассчитана по формуле:
 ,
,
где Wx – осевой момент сопротивления сечения.
Осевые моменты сопротивления Wx и площади сечений, показанных на рисунке 8, определяют по формулам:
прямоугольник: 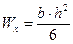 ; S = b·h;
; S = b·h;
квадрат  ; S =h2;
; S =h2;
круг:  ; S = πd 2/4;
; S = πd 2/4;
кольцо:  ; S = π (d 2–d0) /4;
; S = π (d 2–d0) /4;
двутавр – смотри рисунок 9 и таблицу 6. Заметим, что именно двутавр обеспечивает наилучшее сопротивление изгибу.

Рисунок 9 – Параметры сечения двутавра
Таблица 5 – Характеристики двутавров
| Номер балки | Масса G 1метр кг | h, мм | b, мм | s, мм | t, мм | R, мм | r, мм | Площадь сечения S, мм2 | Момент сопротив ления Wх, мм3 | |
| 9,46 | 4,5 | 7,2 | 7,0 | 2,5 | 12,0·102 | 39,7·103 | ||||
| 11,5 | 4,8 | 7,3 | 7,5 | 3,0 | 14,7·102 | 58,4·103 | ||||
| 13,7 | 4,9 | 7,5 | 8,0 | 3,0 | 17,4·102 | 81,7·103 | ||||
| 15,9 | 5,0 | 7,8 | 8,5 | 3,5 | 20,2·102 | 109·103 | ||||
| 18,4 | 5,1 | 8,1 | 9,0 | 3,5 | 23,4·102 | 143·103 | ||||
| 18а | 19,9 | 5,1 | 8,3 | 9,0 | 3,5 | 25,4·102 | 159·103 | |||
| 21,0 | 5,2 | 8,4 | 9,5 | 4,0 | 26,8·102 | 184·103 | ||||
| 20а | 22,7 | 5,2 | 8,6 | 9,5 | 4,0 | 28,9·102 | 203·103 | |||
| 24,0 | 5,4 | 8,7 | 10,0 | 4,0 | 30,6·102 | 232·103 | ||||
| 22а | 25,8 | 5,4 | 8,9 | 10,0 | 4,0 | 32,8·102 | 254·103 | |||
| 27,3 | 5,6 | 9,5 | 10,5 | 4,0 | 34,8·102 | 289·103 | ||||
| 24а | 29,4 | 5,6 | 9,8 | 10,5 | 4,0 | 37,5·102 | 317·103 | |||
| 31,5 | 6,0 | 9,8 | 11,0 | 4,5 | 40,2·102 | 371·103 | ||||
| 27а | 33,9 | 6,0 | 10,2 | 11,0 | 4,5 | 43,2·102 | 407·103 | |||
| 36,5 | 6,5 | 10,2 | 12,0 | 5,0 | 46,5·102 | 472·103 | ||||
| 30а | 39,2 | 6,5 | 10,7 | 12,0 | 5,0 | 49,9·102 | 518·103 | |||
| 42,2 | 7,0 | 11,2 | 13,0 | 5,0 | 53,8·102 | 597·103 | ||||
| 48,6 | 7,5 | 12,3 | 14,0 | 6,0 | 61,9·102 | 743·103 | ||||
| 57,0 | 8,3 | 13,0 | 15,0 | 6,0 | 72,6·102 | 953·103 | ||||
Для выполнения задания необходимо:
1) рассчитать максимальный изгибающий момент, (Н мм):
Mu мах= FL;
2) рассчитать осевой момент сопротивления в опасном сечении, (мм3):
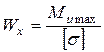 ;
;
3) рассчитать характерный размер сечения балки для выбранных вариантов формы сечения, используя формулы, связывающие этот размер с Wx, или определить № двутавра по таблице 5.
Изобразить сечения в масштабе;
4) рассчитать площадь сечения S и массу G (G = S·L·ρ, кг) балки для выбранных вариантов формы ее сечения.
Задание 6
Выполнить ориентировочный проектный расчет вала (рисунок 10) на прочность и рассчитать шпонку. Значения параметров приведены в таблице 7.



1 – вал; 2 – втулка; 3 – шпонка.
Рисунок 10 – Соединение вала с полумуфтой призматической шпонкой
Таблица 7 – Варианты задания 6
| Переменные параметры | |||||||||
| Крутящий момент Т, Нм | Последняя цифра шифра | ||||||||
| Предпоследняя цифра шифра | |||||||||
| Количество шпонок | |||||||||
| Материал колеса | сталь | чугун | сталь | чугун | сталь |
1 Расчет вала. На первом этапе проектирования диаметр d (мм) консольного участка вала редуктора определяем расчетом на чистое кручение по пониженным допускаемым напряжениям [τ]:
 ,
,
где Т · 103 – вращающий момент, передаваемый валом, Н·мм;
[τ]= 15…30 МПа, допускаемые касательные напряжения. Меньшие значения относятся к входным валам, большие к выходным.
Например, для Т = 500 Н·м (Т = 500 Нмм) и [τ]= 20 МПа диаметр вала:
 (округляем до целого).
(округляем до целого).
Длину конца вала ориентировочно принимаем L = 1,5d = 75 мм.
2 Выбор шпонки. Для обеспечения соединения полумуфты с валом (рисунок 10) нужно выбрать призматическую шпонку по диаметру d вала и определить ее длину l, исходя из данных, приведенных в таблице 8.
Таблица 8 - Размеры шпонок и пазов по (ГОСТ 23360-84)
| Диаметр вала d, мм | Размеры сечения шпонок | Глубина паза | ||
| Ширина b, мм | Высота h,мм | Вал t1, мм | Втулка t2, мм | |
| от 6 до 8 | 1,2 | 1,0 | ||
| св. 8-10 | 1,8 | 1,4 | ||
| св. 10-12 | 2,5 | 1,8 | ||
| св. 12-17 | 2,3 | |||
| св. 17-22 | 3,5 | 2,8 | ||
| св. 22-30 | 3,3 | |||
| св. 30-38 | 3,3 | |||
| св. 38-44 | 3,3 | |||
| св. 44-50 | 5,5 | 3,8 | ||
| св. 50-58 | 4,3 | |||
| св. 58-65 | 4,4 | |||
| св. 65-75 | 7,5 | 4,9 | ||
| св. 75-85 | 5,4 | |||
| св. 85-95 | 5,4 | |||
| св. 95-110 | 6,4 |
Примечание: Длины призматических шпонок (мм) выбирают из ряда (по ГОСТ 23360-84): 6; 8; 10; 12; 14; 16; 18; 20; 22; 25; 28; 32; 36; 40; 45; 50; 56; 63; 70; 80; 90; 100; 110; 125; 140; 160; 180; 200; 220; 250; 280; 320.
В рассматриваемом примере диаметр вала d =50 мм, L = 75 мм. По таблице 8 определяем размеры шпонки и шпоночных пазов вала и полумуфты.
Сечение шпонки: b =14 мм, h = 9 мм.
Глубина паза вала: t1 = 5,5 мм.
Глубина паза ступицы: t2 = 3,8 мм.
Длина l = 70 мм (l < L, концы шпоночного паза не должны подходить к краям посадочного участка вала ближе 2 – 5мм).
3 Проверочный расчет шпонки
Крутящий момент передается боковыми гранями шпонки. При этом на них возникают напряжения смятия σсм, а в продольном сечении шпонки – напряжения среза τср.
Условие прочности шпоночного соединения на смятие: 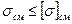 .
.
Допускаемое напряжение смятия [σ]см при ориентировочных расчетах для стальной ступицы (втулки) принимают [σ]см=150-200 МПа, для чугунной – [σ]см= 70-100 МПа.
Действующее напряжение смятия определяется по формуле:
σсм= F1/ Sсм ,
где F1 – окружная сила на поверхности вала, (H), приложенная к одной
шпонке. F1= Т/(d/2) · z;
z – количество шпонок;
Sсм – площадь смятия, мм2. Sсм= (0,94 h – t1) lp;
lp = l-b – рабочая длина шпонки со скругленными торцами, мм.
В рассматриваемом примере при z=1:
F1 = 500·103/ 25 = 20000 Н;
lp = 70 -14= 56 мм;
Sсм=(0,94·9 – 5,5)·56=170 мм2;
σсм= 20000/170= 112 H/мм2.
112 <150 H/мм2. Условие прочности шпонки на смятие выполнено.
Условие прочности шпонки на срез: τср  [τ]ср ,
[τ]ср ,
где [τ]ср – допускаемое напряжение среза. При ориентировочных расчетах для стальной шпонки можно принять [τ]ср = 90 МПа.
Действующее напряжение среза τср определяется по формуле:
τср = F1/ Sср ,
где Sср – площадь среза (Sср= b·lp).
В рассматриваемом примере получаем:
Sср = 14·56 = 785 мм2;
τср = 20000/785=25,5 Н/мм2.
25,5 < 90 H/мм2, следовательно условие прочности шпонки на срез выполнено.
По результатам расчета изобразить в масштабе поперечное сечение вала со шпонкой (подобно сечению А-А на рисунке 10).
СПИСОК ЛИТЕРАТУРЫ
1 Теория механизмов и машин / К. В. Фролов, С. А. Попов, А. К. Мусатов [и др.]; под ред. К. В. Фролова. – М.: Высш. шк., 2001. – 496 с.
2 Прикладная механика: учебник для вузов / В. В. Джамай, Ю. Н. Дроздов, Е. А. Самойлов [и др.]; под ред. В. В. Джамая. – М.: Дрофа, 2004. – 414 с.
3 Артоболевский, И.И. Теория механизмов и машин [Текст] /И.И. Артоболевский.: – М.: Наука, 1990. – 638 с.
Глеб Юрьевич Волков
Лариса Николаевна Тютрина
Дмитрий Алексеевич Курасов
ПРИКЛАДНАЯ МЕХАНИКА
Задачи и методические указания
к выполнению контрольных работ
для студентов направлений:
140400.62, 220400.62, 220700.62,
221700.62, 222000.62
Редактор Е.А. Могутова
Подписано впечать Формат 60 х 84 1/16 Бумага 65 г/м2
Печать цифровая Усл.печ.л. 1,5 Уч-изд.л 1,5
Заказ Тираж 25
РИЦ Курганского государственного университета
640000, г. Курган, ул. Советская, 63/4
Курганский государственный университет.
Date: 2016-07-25; view: 492; Нарушение авторских прав