Главная Случайная страница


Полезное:

Как сделать разговор полезным и приятным Как сделать объемную звезду своими руками Как сделать то, что делать не хочется? Как сделать погремушку Как сделать так чтобы женщины сами знакомились с вами Как сделать идею коммерческой Как сделать хорошую растяжку ног? Как сделать наш разум здоровым? Как сделать, чтобы люди обманывали меньше Вопрос 4. Как сделать так, чтобы вас уважали и ценили? Как сделать лучше себе и другим людям Как сделать свидание интересным?


Категории:

АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника






Элементы математической статистики

 

Решение типового варианта

Задание I

В результате эксперимента получены данные, записанные в виде статистического ряда:

Требуется:

1). записать значения результатов эксперимента в виде вариационного ряда;

2). найти размах варьирования и разбить его на ряд частичных интервалов;

3). построить полигон частот, гистограмму относительных частот и график эмпирической функции распределения;

4). найти числовые характеристики выборки (математическое ожидание, дисперсию, среднее квадратическое отклонение);

5). приняв в качестве нулевой гипотезу : генеральная совокупность, из которой извлечена выборка, имеет нормальное распределение, проверить её, критерием Пирсона при уровне значимости ;

6). найти доверительные интервалы для математического ожидания и среднего квадратичного отклонения при надежности .

 

44,8 46,2 45,6 44,0 46,4 45,2 46,7. 45,4 45,3 46,1
44,3 45,3 45,6 46,7 44,5 46,0 45,7 45,0 46,4 45,9
44,4 45,4 46,1 43,4 46,5 45,9 43,9 45,7 47,1 44,9
43,8 45,6 45,2 46,4 44,2 46,5 45,7 44,7 46,0 45,8
44,3 45,5 46,7 44,9 46,2 46,7 44,6 46,0 45,4 45,0
45,4 45,3 44,1 46,6 44,8 45,6 43,7 46,8 45,2 46,1
44,5 45,4 45,1 46,2 44,2 46,4 45,7 43,9 47,2 45,0
43,9 45,6 44,9 44,5 46,2 46.7 44,3 46,1 47,7 45,8
45,6 45,2 44,2 46,0 44,7 46,5 43,5 45,4 47,1 44,0
46,2 44,2 45,5 46,0 45,7 46,4 44,6 47,0 45,2 46,9

 


Решение:

1). Располагаем значение результатов эксперимента в порядке возрастания, т.е. записываем вариационный ряд:

 

43,4 43,5 43,7 43,8 43,9 43,9 43,9 44,0 44,0 44,1
44,2 44,2 44,2 44,3 44,3 44,3 44,4 44,5 44,5 44,5
44,6 44,6 44,7 44,7 44,8 44,8 44,8 44,9 44,9 44,9
45,0 45,0 45,1 45,2 45,2 45,2 45,2 45,2 45,3 45,3
45,3 45,4 45,4 45,4 45,4 45,4 45,4 45,5 45,5 45,6
45,6 45,6 45,6 45,6 45,7 45,7 45,7 45,7 45,7 45,7
45,8 45,8 45,9 45,9 46,0 46,0 46,0 46,0 46,0 46,0
46,1 46,1 46,1 46,1 46,2 46,2 46,2 46,2 46,2 46,4
46,4 46,4 46,4 46,4 46,5 46,5 46,5 46,6 46,7 46,7
46,7 46,7 46,7 46,8 46,9 47,0 47,1 47,1 47,2 47,7

 

2). Находим размах варьирования: .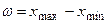

Иногда для определения данных интервала используют формулу , где - объем выборки. За величину частичного интервала принимается некоторое удобное число, ближайшее к полученному . Число таких интервалов определяется формулой . В качестве границы первого интервала можно выбрать значение . Тогда границы следую­щих частичных интервалов вычисляем по формуле , где принимает значения от 1 до .

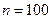В нашем примере . Объём выборки , тогда . Примем за . Следовательно, разобьем наш вариационный ряд на интервалов.

Находим середины интервалов: . Подсчитываем число значений результатов эксперимента, по­павших в каждый интервал, т.е. находим частоты интервалов .Далее вычисляем относительные частоты и их плотности . Все полученные результаты помещаем в таблицу (табл. 1).

Таблица 1.

Номер частичного ин­тервала i Границы интервала Середина интервала Частота интер­вала Относитель­ная частота Плотность относитель- ной частоты
  43,40 – 43,96 43,68   0,07 0,13
  43,96 – 44,52 44,24   0,13 0,23
  44,52 – 45,08 44,80   0,12 0,21
  45,08 – 45,64 45,36   0,22 0,39
  45,64 – 46,20 45,92   0,25 0,45
  46,20 – 46,76 46,48   0,14 0,25
  46,76 – 47,32 47,04   0,06 0,11
  47,32 – 47,88 47,60   0,01 0,02
  –   –  

 

3). Строим полигон частот – ломанную линию, отрезки которой соединяют точки , , …, (рис. 1) и гистограмму относительных частот – ступенчатую фигуру, состоящую из прямоугольников, основаниями которой служат частичные интервалы, длиною , а высоты равны плотности относительной частоты (рис.2).

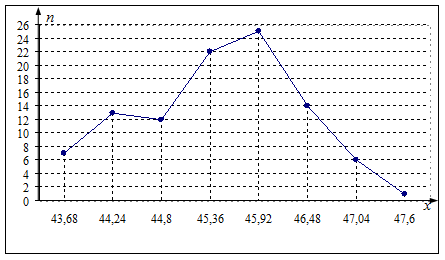
Рис. 1. Полигон частот

 

Рис.2. Гистограмма относительных частот

Найдем значения эмпирической функции распределения (функции распределения выборки) – функции, определяющей для каждого значения относительную частоту события .

Итак, по определению,

,

где - число вариант, меньших ; - объём выборки.

, , ,

, , ,

, , .

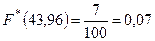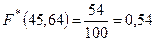Строим график эмпирической функции распределения (рис. 3).

Рис. 3. График эмпирической функции распределения

 

4). Находим выборочное среднее: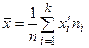

и выборочную дисперсию: .

Для этого составляем расчетную таблицу (табл. 2).

Таблица 2.

 

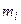
Границы интервала Середина интервала Частота интер­вала
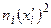
  43,40 – 43,96 43,68   305,76 1907,94 13355,60
  43,96 – 44,52 44,24   575,12 1957,18 25443,31
  44,52 – 45,08 44,80   537,60 2007,04 24084,48
  45,08 – 45,64 45,36   997,92 2057,53 45265,65
  45,64 – 46,20 45,92   1148,00 2108,65 52716,16
  46,20 – 46,76 46,48   650,72 2160,39 30245,47
  46,76 – 47,32 47,04   282,24 2212,76 13276,57
  47,32 – 47,88 47,60   47,60 2265,76 2265,76
  –   4544,96 –  

Из нее получаем: , , .

Несмещённой называют статистическую оценку , математическое ожидание которой равно оцениваемому параметру при любом объёме выборки.

Смещённой называют оценку, математическое ожидание которой не равно оцениваемому параметру.

Выборочная дисперсия является смещенной оценкой гене­ральной дисперсии, а исправленная дисперсия - несмещенной оценкой:

, .

5). Критерием согласия называют критерий проверки гипотезы о предполагаемом законе неизвестного распределения. Имеется несколько критериев согласия: («хи квадрат») К. Пирсона, Колмагорова, Фишера, Смирнова и др.

По условию задачи нам необходимо использовать критерий Пирсона, правило применения которого сводится к следующему:

1. вычислить теоретические частоты, затем наблюдаемое значение критерия по формуле ;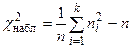

2. по таблице критических точек распределения , по заданному уровню значимости и числу степеней свободы , где – число интервалов, найти критическую точку ;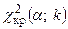

3. если – нет оснований отвергать нулевую гипотезу;

если 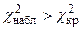– нулевую гипотезу отвергают.

Согласно критерию Пирсона необходимо сравнить эм­пирические и теоретические частоты. Эмпирические частоты даны. Найдем теоретические частоты. Для этого пронумеруем ,т.е. перейдем к случайной величине и вычислим концы ин­тервалов: и . Наи­меньшее значение положим стремящимся к , а наибольшее – , стремящимся к . Результаты занесем в таблицу (табл. 3). Число наблюдений в отдельных интервалах должно быть достаточно большим (рекомендуется иметь в каждом интервале не менее 5-10 наблюдений). Если в отдельных интервалах очень малы, следует объединить интервалы. Длины интервалов могут быть различными. В соответствии с этим число исходных интервалов может быть уменьшено. Так как , то последний девятый интервал объединим с восьмым и получим интервал с частотой .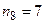

Таблица 3.

Границы интервала Границы интервала
  43,40 44,96 – -0,49 -1,31
  43,96 44,52 -0,49 -0,93 -1,31 -1,02
  44,52 45,08 -0,93 -0,37 -1,02 -0,41
  45,08 45,64 -0,37 0,19 -0,41 0,21
  45,64 46,20 0,19 0,75 0,21 0,82
  46,20 46,76 0,75 1,31 0,82 1,44
  46,76 47,88 1,31 – 1,44
             

Находим теоретические вероятности и теоретические частоты: . Составляем расчетную таблицу (табл. 4). Значения функции берём из прил.1.

Таблица 4.

 

 

 

Границы интервала
  -1,31 -0,5000 -0,4049 0,0951 9,51
  -1,31 -1,02 -0,4049 -0,3461 0,0588 5,88
  -1,02 -0,41 -0,3461 -0,1591 0,1870 18,70
  -0,41 0,21 -0,1591 0,0832 0,2423 24,23
  0,21 0,82 0,0832 0,2939 0,2107 21,07
  0,82 1,44 0,2939 0,4251 0,1312 13,12
  1,44 0,4251 0,5000 0,0749 7,49
– – – –    

Вычислим наблюдаемое значение критерия Пирсона. Для этого составим расчетную таблицу (табл. 5). Последние два столбца служат для контроля вычислений по формуле:

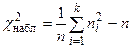
Таблица 5

 

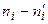
    9,51 -2,51 6,3001 0,6625   5,1525
    5,88 7,12 50,6944 8,6215   28,7415
    18,70 -6,70 44,89 2,4005   7,7005
    24,23 -2,23 4,9729 0,2052   19,9752
    21,07 3,93 15,4449 0,7330   29,6630
    13,12 0,88 0,7744 0,0590   14,9390
    7,49 -0,49 0,2401 0,0321   6,5421
    – – 12,7138 – 112,7138

 

Контроль: .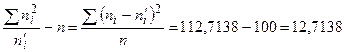

По таблице критических точек распределения (см. прил. 3), уровню значимости и числу степеней свободы 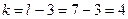( – число интервалов) нахо­дим: .

Так как , то гипотеза о нормальном распре­делении генеральной совокупности принимается.

 

6). Если случайная величина генеральной совокупности распределена нор­мально, то с надежностью можно утверждать, что математи­ческое ожидание случайной величины покрывается доверительным интервалом ,где – точностьоценки. Значение определяется из условия , т.е. .

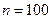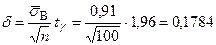В нашем случае: , , , , . Из прил.1 находим , . Доверитель­ным интервалом для будет . Доверитель­ный интервал, покрывающий среднее квадратичное отклоне­ние с заданной надежностью : ,где находится по данным и из прил. 2. При и 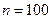имеем: . Доверительным интервалом для будет .

 

Задание II

Дана таблица распределения 100 заводов по производственным средствам (тыс. ден. Ед.) и по суточной выработке (т). Известно, что между и существует линейная корреляционная зависимость. Требуется:

1. найти уравнение прямой регрессии на ;

2. построить уравнение эмпирической линии регрессии и случайные точки выборки ;

4,5 6,0 7,5 9,0 10,5 12,0 13,5  
            — — —  
  — —       — — —  
  — — — —       —  
  — — — — —        
  — — — — —        
  — — — — —        
                 

Решение:

Для подсчёта числовых характеристик (выборочных средних и , выборочных средних квадратичных отклонени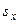й и и выборочного корреляционного момента ) составляем расчётную таблицу (табл.6). При заполнении таблицы осуществляем контроль по строкам и столбцам:

,

, ,

.

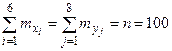Вычисляем выборочные средние и , ; :

, .

Выборочные дисперсии находим по формулам:

,

.

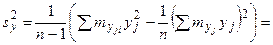
Корреляционный момент вычисляем по формулам:

.

Оценкой теоретической линии регрессии является эмпирическая линия регрессии, уравнение которой имеет вид:

,

где ; ; .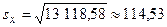

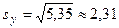Составляем уравнение эмпирической линии регрессии на :

,

.

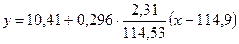Строим линию регрессии и случайные точки (рис.4).

Рис. 4.


Таблица 6.

                           
4,5 6,0 7,5 9,0 10,5 12,0 13,5  
              — — —     187,5    
    — —       — — —     223,5    
    — — — —       —     292,5    
    — — — — —           166,5    
    — — — — —           103,5    
    — — — — —           67,5    
                           
      67,5       148,5     — — — —
                    — — — —
  40,5   506,25   2866,5   2004,7     — — — —
                    — — — —

Задание I

В результате эксперимента получены данные, записанные в виде статистического ряда. Требуется:

1). записать значения результатов эксперимента в виде вариационного ряда;

2). найти размах варьирования и разбить его на ряд частичных интервалов;

3). построить полигон частот, гистограмму относительных частот и график эмпирической функции распределения;

4). найти числовые характеристики выборки (математическое ожидание, дисперсию, среднее квадратическое отклонение);

5). приняв в качестве нулевой гипотезу : генеральная совокупность, из которой извлечена выборка, имеет нормальное распределение, проверить её, критерием Пирсона при уровне значимости α =0,025;

6). найти доверительные интервалы для математического ожидания и среднего квадратичного отклонения при надежности γ = 0,99.

 

 

Задание II

Дана таблица распределения 100 заводов по производственным средствам (тыс. ден. Ед.) и по суточной выработке (т). Известно, что между и существует линейная корреляционная зависимость. Требуется:

1. найти уравнение прямой регрессии на ;

2. построить уравнение эмпирической линии регрессии и случайные точки выборки .

 

Вариант 1

1.1

17,1 21,4 15,9 19,1 22,4 20,7 17,9 18,6 21,8 16,1
19,1 20,5 14,2 16,9 17,8 18,1 19,1 15,8 18,8 17,2
16,2 17,3 22,5 19,9 21,1 15,1 17,7 19,8 14,9 20,5
17,5 19,2 18,5 15,7 14,0 18,6 21,2 16,8 19,3 17,8
18,8 14,3 17,1 19,5 16,3 20,3 17,9 23,0 17,2 15,2
15,6 17,4 21,3 22,1 20,1 14,5 19,3 18,4 16,7 18,2
16,4 18,7 14,3 18,2 19,1 15,3 21,5 17,2 22,6 20,4
22,8 17,5 20,2 15,5 21,6 18,1 20,5 14,0 18,9 16,5
20,8 16,6 18,3 21,7 17,4 23,0 21,1 19,8 15,4 18,1
18,9 14,7 19,5 20,9 15,8 20,2 21,8 18,2 21,2 20,1

2.1

2,2 3,6 5,0 6,4 7,8 9,2 10,6  
        — — — — —  
  —     — — — — —  
  — —       — — —  
  — — —       — —  
  — — — —       —  
  — — — — — —      
                 

Вариант 2

1.2

16,8 17,9 21,4 14,1 19,1 18,1 15,1 18,2 20,3 16,7
19,5 18,5 22,5 18,4 16,2 18,3 19,1 21,4 14,5 16,1
21,5 14,9 18,6 20,4 15,2 18,5 17,1 22,4 20,8 19,8
17,2 19,7 16,3 18,7 14,4 18,8 19,5 21,6 15,3 17,3
22,8 17,4 22,2 16,5 21,7 15,4 21,3 14,3 20,5 16,4
20,6 15,5 19,4 17,5 20,9 23,0 18,9 15,9 18,2 20,7
17,9 21,8 14,2 21,2 16,1 18,4 17,5 19,3 22,7 19,6
22,1 17,6 16,7 20,4 15,7 18,1 16,6 18,3 15,5 17,7
19,2 14,8 19,7 17,7 16,5 17,8 18,5 14,0 21,9 16,9
15,8 20,8 17,1 20,1 22,6 18,9· 15,6 21,1 20,2 15,1

2.2

2,3 3,8 5,3 6,8 7,3 8,8 10,3 11,8
  —       — — — —  
  —       — — — —  
  — —       — — —  
  — — — —       —  
  — — — — —     —  
  — — — — — —      
—                

Вариант 3

1.3

                   
                   
                   
                   
                   
                   
                   
                   
                   
                   

2.3

22,0 22,4 22,8 23,2 23,6 24,0 24,4 24,8
1,00       — — — — —  
2,20 — —     — — — —  
1,40 — —       — — —  
1,60 — — —       — —  
1,80 — — — —       —  
2,00 — — — — —        
                 

Вариант 4

1.4

9,4 7,9 0,3 6,8 4,2 11,9 7,8 1,7 5,1 8,8
8,7 11,1 7,7 1,8 5,5 10,5 4,3 3,8 1,4 11,2
1,1 7,3 3,7 4,4 11,8 8,6 1,9 5,6 10,1 8,4
10,0 11,6 5,2 2,1 5,7 4,8 7,4 0,8 4,7 3,6
8,3 7,6 0,7 7,3 3,4 11,4 5,7 9,9 2,2 7,2
2,3 4,7 9,7 11,3 5,8 4,9 3,3 0,5 7,5 4,6
5,0 0,4 8,9 7,1 9,6 11,5 5,9 9,0 5,3 2,4
9,5 5,9 1,0 9,1 2,5 6,0 8,2 3,2 10,9 6,1
10,2 2,6 4,5 3,1 6,2 11,7 6,3 0,2 7,0 9,2
1,2 6,4 11,9 6,9 8,1 6,5 2,9 6,2 4,4 10,3

2.4

21,0 21,3 21,6 21,9 22,2 22,5 22,8 23,1
0,90       — — — — —  
1,05 —       — — — —  
1,20 — —       — — —  
1,35 — — —       — —  
1,50 — — — —       —  
1,65 — — — — —        
                 

Вариант 5

1.5

1,6 4,4 10,9 6,4 4,0 2,8 5,2 1,2 7,6 3,4
2,9 5,3 1,7 7,7 6,9 10,1 5,4 4,1 8,8 6,5
6,6 4,2 5,5 0,5 8,9 4,5 1,8 5,6 7,8 3,0
1,9 10,2 7,9 2,5 5,7 3,1 6,7 4,3 0,6 9,0
6,8 3,2 4,4 9,1 10,3 6,0 7,9 6,9 8,0 2,0
7,0 10,7 8,1 2,1 5,8 6,4 0,3 4,5 9,2 3,3
7,6 9,3 3,4 4,6 5,0 3,8 5,9 8,2 2,2 7,1
2,3 0,8 7,2 8,3 11.1 6,5 3,5 9,4 10,8 4,7
4,8 6,1 3,6 9,5 8,4 2,4 6,2 7,3 5,7 0,9
7,4 8,5 5,8 1,1 5,9 4,9 3,7 9,6 2,6 6,1

 

2.5

               
1,0       — — — — —  
1,3 —
<== предыдущая | следующая ==>
по согласованию с преподавателями. | 

Date: 2016-07-25; view: 3705; Нарушение авторских прав; Помощь в написании работы --> СЮДА...


mydocx.ru - 2015-2024 year. (0.012 sec.) Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав - Пожаловаться на публикацию