Обнаружение и анализ эллиптически- и циркулярно-поляризованного света

Обнаружение особенностей эллиптически-поляризованного света связано с известными трудностями.

Применив для анализа света какое-нибудь поляризационное устройство, мы получим следующие результаты. Сквозь поляризатор пройдет только часть света, соответствующая компоненте колебаний пропускаемых им; нетрудно видеть, что амплитуда прошедшего света зависит от ориентации главной плоскости поляризатора NN по отношению к осям эллипса.

Амплитуда А равна половине длины стороны прямоугольника, параллельной NN. в который вписан эллипс. При повороте николя поворачивается и прямоугольник.

Амплитуда будет максимальной (А = b); когда плоскость NN совпадает с большой осью эллипса, и минимальной (А = а), если она параллельна малой оси. Поэтому при вращении поляризатора мы получим частичное затемнение или просветление поля, т. е. будет наблюдаться та же картина, как и при исследовании поляризатором частично поляризованного света. В частности, если свет поляризован по кругу, т. е. а = b, то вращение поляризатора совсем не будет влиять на интенсивность проходящего света, т. е. мы увидим ту же картину, как и при исследовании поляризатором естественного света. Таким образом, анализ при помощи поляризатора не позволяет отличить эллиптически-поляризованный свет от частично поляризованного, а циркулярно-поляризованный — от естественного.

Для полного анализа необходимо превратить эллиптически- или циркулярно-поляризованный свет в плоскополяризованный, анализ которого легко выполняется при помощи поляризационной призмы.

Способ получения плоскополяризованного света из излучения эллиптической или круговой поляризацией ясен из рассмотрения соотношений, приведенных в предыдущем пункте. Достаточно компенсировать разность фаз φ между перпендикулярными компонентами, доведя ее до π или 2π (или до нуля). Для этой цели можно заставить изучаемый свет пройти через вспомогательную кристаллическую пластинку подходящей толщины или ориентации.

а. Применение пластинки в 1/4 волны для компенсации разности фаз. В эллиптически-поляризованном световом пучке между компонентами, направленными вдоль главных осей эллипса (а в циркулярно-поляризованном— между компонентами, направленными вдоль двух произвольно выбранных взаимно перпендикулярных диаметров), существует разность фаз π/2. Заставляя иследуемый свет пройти через пластинку в 1/4λ, мы добавим к этой разности ±π/2, т. е. скомпенсируем имеющуюся разность фаз, обращая ее в нуль или в π. Таким образом, исследуемый свет превращается в плоскополяризованный, в чем можно убедиться при помощи обычного поляризатора. Для указанной цели в случае циркулярно-поляризованного пучка можно ориентировать пластинку в 1/4λ, как угодно; в случае эллиптически-поляризованного пучка надо ориентировать ее так, чтобы главные направления пластинки совпадали с главными осями эллипса, определенными предварительно при помощи поляризатора. Таким образом, анализ выполняется при помощи пластинки в 1/4λ и поляризатора. Указанным приемом можно также определить направление вращения (правая и левая поляризации), для чего необходимо лишь предварительно знать, какое из двух колебаний в использованной пластинке в 1/4λ, распространяется с большей скоростью.

б. Применение компенсаторов для анализа эллиптически-поляризованного света. Для полного количественного анализа эллиптически-поляризованного света надо знать форму и расположение эллипса по отношению к любым направлениям, т. е. разность фаз двух взаимно перпендикулярных компонент любого направления.

Для этой цели служат приборы, способные скомпенсировать до нуля (или дополнить до я) любую разность фаз. Такие приборы называются компенсаторами. В качестве примера рассмотрим компенсатор Бабине. Он состоит из двух клиньев, обычно из кварца, вырезанных так, что оси их ориентированы под прямым углом друг к другу.

Свет, проходящий в разных местах через компенсатор, получает ту или иную добавочную разность хода между двумя компонентами колебаний светового вектора в зависимости от разности толщин клиньев в данном месте. Обозначив толщину в первой половине клина через d₁, а во второй — через d₂ найдем, что добавочная разность хода между компонентами (одной — лежащей в плоскости чертежа и другой — перпендикулярной к нему) равна

.

Таким образом, в компенсаторе из положительного кристалла (n_e > n_o) свет, проходящий по линии, где d₁ > d₂, приобретает добавочную разность хода; по линии, где d₁ = d₂, первоначальная разность хода остается неизменной; по линии, где d₁ < d₂ разность хода уменьшается.

Эллиптически-поляризованный свет, проходя через определенные места компенсатора, дополняющие разность фаз компонент, параллельных главным плоскостям компенсатора, до 0, 2π, 4π и т. д., обращается в линейно-поляризованный свет одного направления. Легко видеть, что такие участки компенсатора расположены на равных расстояниях друг от друга. Если за компенсатором В поставить поляризатор N, ориентированный соответствующим образом, то все эти места окажутся темными (ряд темных равноотстоящих полос, параллельных ребру компенсатора). При другой ориентации поляризатора можно получить ряд темных равноотстоящих полос, соответствующих местам компенсатора, где дополняющая разность фаз доводит начальную разность фаз до π, Зπ, 5π и т. д.

Зная толщину клиньев и материал, из которого они сделаны, можно рассчитать (или предварительно проградуировать) добавляемую разность фаз и таким образом определить разность фаз, которая характеризовала данный эллиптический свет. Часто клинья делают подвижными друг относительно друга и тогда вычисление ведется по сдвигу клиньев, приводящему к определенному расположению полос, например, к появлению темной полосы в центре поля (на кресте окуляра). Для практической работы удобнее компенсаторы, вся поверхность поля зрения которых представляет область одной и той же добавочной фазы, причем последнюю можно по желанию изменять.

Так как при всех методах количественного исследования поляризованного света требуется определение угла поворота (поляризатора, пластинки в 1/4λ или компенсатора), то обычно поляризационные приборы снабжаются оправами с хорошими угловыми делениями.

Вращение плоскости поляризации

Вещества, обладающие способностью вращать плоскость поляризации, называют оптически активными. Этот эффект наблюдается у ряда кристаллических и аморфных тел. Начнем наше рассмотрение с анализа экспериментального материала.

1. Опыты с кварцем. Классическим объектом для демонстрации вращения плоскости поляризации служит одноосный кристалл. Схема опыта представлена на рис.Поляризатор и анализатор установлены так, что они не пропускают излучения (скрещены). После введения пластинки кварца толщиной d поле просветляется. Свет распространяется вдоль оптической оси кварца, и, следовательно, двойное лучепреломление отсутствует. Повернув анализатор на угол φ, снова получаем темноту, что доказывает наличие в данном случае именно поворота плоскости поляризации, а не какого-то другого явления (например, при возникновении эллиптической поляризации было бы невозможно погасить свет вращением анализатора). Опыт показывает, что разные образцы кварца вращают плоскость поляризации вправо или влево (если смотреть навстречу световому лучу). Таким образом, различают правое вращение (по часовой стрелке) и левое вращение (против часовой стрелки). Не пытаясь пока объяснить этот процесс, укажем, что кристаллы правовращающего и левовращающего кварца отличаются по своей форме и являются зеркальным отображением друг друга.

Опыт дает , причем коэффициент , т.е. сильно зависит от длины волны падающего на кристалл света. (Так, при d = 1 мм имеем φ_желт≈20°, а φ_фиол≈50°). Следовательно, вращение плоскости поляризации света кварцем — это эффект, который легко наблюдается.

2. Опыты с аморфными веществами (сахар, камфара, патока, никотин и др.). Опыт ставится так же, как и в предыдущем случае, но вместо кварца между поляризаторами вводят кювету с оптически активным веществом. Если обозначить длину кюветы через d, а концентрацию вещества — через с, то из опыта получается , где [α] —- постоянная вращения для данного вещества, сильно зависящая от длины волны () и слабо — от температуры образца. Постоянная вращения [α] практически не зависит от агрегатного состояния вещества.

Подобные опыты лежат в основе метода определения концентрации оптически активного вещества при измерении угла вращения плоскости поляризации. Метод имеет многочисленные приложения. В частности, им пользуются

для нахождения концентрации сахара в

производственных

растворах и биологических

объектах (кровь, моча).

Интерпретация вращения плоскости поляризации

была дана впервые Френелем, показавшим, что оно в какой-то степени аналогично двойному лучепреломлению. При изложении сущности формальной теории Френеля прежде всего установим, что любое линейно поляризованное колебание можно разложить на два круговых колебания с правым и левым вращением. Это ясно из геометрического построения, приведенного на рис. Действительно, сумма двух векторов («левого» и «правого») равна удвоенной проекции любого из них на диаметр, т.е. вектору, направление которого постоянно, а модуль изменяется по периодическому закону с частотой ω. Это и есть линейно поляризованное колебание.

Френель предположил, что в оптически активном веществе скорость распространения волны с правым вращением отлична от скорости распространения волны с левым вращением, т.е. u_пр≈u_лев. В связи с этим все оптически активные вещества можно подразделить на «правые» (u_пр>u_лев) и «левые» (u_пр<u_лев).

Рассмотрим, что произойдет с линейно поляризованной волной, распространяющейся в оптически активной среде. Разложим исходную волну Е на две, поляризованные по правому и левому кругу, скорости распространения которых в данном веществе не равны. Очевидно, что время, необходимое каждой волне для прохождения одного и того же отрезка в исследуемой активной среде, окажется различным. Следовательно, векторы Е_пр и Е_лев повернутся на различные углы φ_пр и φ_лев.

Для того чтобы результирующее колебание осталось линейно поляризованным, неизбежно должна повернуться плоскость симметрии. Для определения направления колебаний в результирующей линейно поляризованной волне нужно сложить две поляризованные по кругу волны после прохождения ими равного пути в оптически активной среде, т.е. найти плоскость симметрии, которая (рис.) должна разделить пополам разность углов φ_пр и φ_лев. Очевидно, что плоскость колебания вектора Е в результирующей плоскополяризованной волне повернется по отношению к направлению колебаний в исходной волне на угол

.

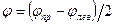Нетрудно получить основные соотношения для угла поворота плоскости поляризации в привычных обозначениях электромагнитной теории.

Основные соотношения для угла поворота плоскости поляризации:

.

Итак, можно считать, что в рамках феноменологической электромагнитной теории света вращение плоскости поляризации получило объяснение. Однако эта теория не способна объяснить почему скорость волны в правовращающем веществе отлична от ее скорости в левовращающем.

Если попытаться ответить на этот вопрос с позиций молекулярной теории, то надо предположить, что вращение плоскости поляризации связано с асимметрией строения оптически активного вещества. В случае кристаллов главной причиной различия скоростей следует считать асимметрию внешней формы (отсутствие центра симметрии). Об этом говорит различие кристалла правого и левого кварца по внешнему виду. Для аморфных однородных тел нужно связать исследуемое явление со строением сложных молекул активной среды.

Этот вопрос был подробно рассмотрен М. Борном (1915), который показал, что описанный выше эффект можно объяснить, если учесть взаимодействие электромагнитного поля с веществом в пределах одной молекулы. При построении теории принималось во внимание, что все оптически активные вещества существуют в двух модификациях, характеризующихся правым и левым вращением плоскости поляризации, и рассматривались сложные асимметричные молекулы с пространственной структурой, не имеющие ни центра симметрии, ни плоскости симметрии.

Механизм магнитного вращения плоскости поляризации.

В рамках излагаемой теории можно исчерпывающе истолковать классические эксперименты Фарадея, впервые наблюдавшего вращение плоскости поляризации в оптически неактивном веществе, помещенном в продольное магнитное поле. Рассмотрим основные результаты таких экспериментов и объясним их с позиций электронной теории.

Опыт проводят по схеме, представленной на рис. Между скрещенными поляризаторами вводят оптически неактивное вещество (например, стержень из стекла специального сорта – флинта), помещенное внутри катушки с большим количеством витков Т или между полюсами мощного магнита с просверленными наконечниками.

При включении электрического тока внутри катушки возникает продольное магнитное поле и на экране наблюдается светлое пятно — свет от внешнего источника S проходит через скрещенные поляризаторы. Вращением анализатора Р₂ можно убедиться, что в данном случае действительно плоскость поляризации поворачивается на некоторый угол φ. При повороте анализатора на угол φ свет не проходит через систему. Угол φ пропорционален напряженности магнитного поля Нвнеш и пути света I в исследуемом веществе:

Коэффициент называют постоянной Верде. Он не одинаков для разных оптических материалов и невелик. Поэтому требуются сильные поля, чтобы эффект был значителен. Обычно в качестве вращающего вещества используют специальные сорта стекла. Коэффициент зависит от длины волны исследуемого света, поэтому для количественных измерений нужно монохроматизировать излучение источника с помощью какого-нибудь фильтра.

Важной особенностью эффекта является его малая инерционность (время установления меньше 10-9 с), а также независимость от направления луча. Отсюда следует, что угол вращения в данном веществе определяется направлением магнитного поля Н_внеш. Последнее свойство (отличающее вращение в магнитном поле от естественного вращения) позволяет увеличить суммарный угол поворота плоскости поляризации системой отражений, на что указывал сам Фарадей.

При изучении явления следует иметь в виду, что в данном случае, как и в предыдущих задачах, нужно рассчитать действие электромагнитной волны на излучающий электрон. При изучении дисперсии вещества учитывалось лишь действие вектора Е, так как в формуле Лоренца второй член в 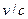раз меньше первого. Но при истолковании эффекта Фарадея необходимо учесть действие внешнего поля Н_внеш, которое во много раз больше напряженности магнитного поля электромагнитной волны. Следовательно, пренебречь уже нельзя.

Пусть все остальные исходные предпосылки полностью соответствуют задаче о вычислении смещения квазиупругосвязанного электрона в поле световой волны. В качестве вынуждающей силы здесь будет фигурировать не произведение qE, а сила Лоренца, которую в данном случае следует записать в виде

Во всех последующих выкладках будем считать Н_внеш = В_внеш Это приближение вполне законно, так как в опытах по искусственному вращению используют прозрачные тела, у которых, как правило, .

На первой стадии рассмотрения эффекта Фарадея пренебрежем затуханием колебаний. Известно, что такое приближение законно вдали от линии поглощения.

Пусть Н_внеш направлено вдоль оси Z и в этом же направлении распространяется световая волна. Напряженность ее электрического поля Е и смещение электрона r лежат в плоскости ХУ, перпендикулярной оси Z. Дифференциальное уравнение осциллирующего электрона в этом случае

Далее, вводя обозначение ,

Следовательно,

Напомним, что исходную линейно поляризованную волну всегда можно разложить на две распространяющиеся в том же направлении циркулярно - поляризованные волны. В этом и заключается физический смысл проведенной математической операции – переход от вещественных уравнений к комплексному уравнению. Если в результате решения уравнения окажется, что показатели преломления для двух циркулярно - поляризованных волн не равны, то будет доказано наличие поворота плоскости поляризации суммарной волны, получающейся в результате сложения двух циркулярно поляризованных волн после прохождения ими в веществе некоторого пути при наличие продольного магнитного поля.

Итак,

,

Решение уравнения ищем в виде:

Находим,

.

Дальнейшие выкладки очевидны:

,

Данная формула содержит решение сформулированной задачи. Для волны, распространяющейся в исследуемой среде, получены два значения показателя преломления: n_пр и n_лев — доказан поворот плоскости поляризации, непосредственно связанный с наличием продольного магнитного поля Н_внеш. Для получения в явном виде измеряемых на опыте величин запишем

Обозначим 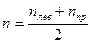и, пренебрегая 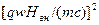, получим:

и далее:

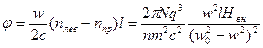
Сравнив это соотношение с экспериментальной формулой, получаем выражение для постоянной Верде в эффекте Фарадея:

При (электронные полосы поглощения лежат в ультрафиолетовой области спектра) можно пренебречь в знаменателе последнего выражения и в согласии с экспериментом получить зависимость постоянной Верде от частоты ρ~ ~ .

Вполне понятна также упоминавшая особенность искусственного вращения: угол поворота не зависит от направления светового пучка и полностью определяется направлением внешнего магнитного поля. Это следует как из формулы, так и из постановки данной задачи, при которой рассматривается не направление Н в электромагнитной волне, а направление Н_внеш внешнего магнитного поля. Можно записать константу Верде в виде:

Представляет интерес искусственное вращение плоскости поляризации при освещении образца излучением, частота которого близка к частоте поглощения исследуемого вещества, т.е. когда затуханием колебаний нельзя пренебречь. Эта задача осложнена тем, что до сего времени мы не интересовались, что происходит со спектральной линией, если источник света или поглощающая среда помещены в магнитное поле. Как было впервые установлено в 1896 г. Зееманом, при этом линия расщепляется на несколько компонент (эффект Зеемана). Число таких компонент, взаимное расположение и относительная интенсивность определяются структурой энергетических уровней, при переходах между которыми возникла исследуемая спектральная линия, и существенно зависят от напряженности приложенного магнитного поля. Эффект Зеемана — важное для спектроскопии и атомной физики явление, которое до конца объясняется с позиций квантовой механики.

При некотором наиболее простом строении атомных уровней возникает нормальный эффект Зеемана, который был объяснен с позиций электронной теории Лоренцем, получившим вместе с Зееманом за это открытие Нобелевскую премию по физике в 1902 г. При нормальном эффекте Зеемана линия расщепляется на две компоненты, если наблюдение ведется вдоль поля (рис. а), или на три компоненты, если оно проводится перпендикулярно линиям напряженности магнитного поля (рис. б). Опыт показывает, что смещенные компоненты поляризованы по правому и левому кругам, а несмещенная линейно поляризована.

Получим этот результат из представлений электронной теории, а затем используем его для изучения изменения показателя преломления вблизи спектральной линии, расщепившейся на две компоненты в продольном магнитном поле. Это позволит истолковать эффект вращения плоскости поляризации вблизи линии поглощения. Хотя нас интересует расщепление линии поглощения, рассмотрим более простой случай — расщепление линии испускания. Рассчитаем, как изменится частота колебаний упруго связанного электрона при действии на него магнитного поля Н_внеш, направленного вдоль оси Z. Положим Е = 0, так как будет рассчитываться лишь изменение движения электрона при наложении внешнего магнитного поля:

В направлении оси Z электрон колеблется так же, как и раньше, — составляющая векторного произведения вдоль оси Z равна нулю. Вводя обозначение , получим в плоскости XY:

Решением такого уравнения, описывающего круговое колебание, служит выражение вида . В результате получаем уравнение, из которого и определим искомое изменение частоты:

Легко показать, что второй член здесь мал по сравнению с двумя другими. Положим . В этом приближении получаем окончательный результат:

Мы установили, что при данной постановке опыта (наблюдение ведется вдоль внешнего магнитного поля) линия испускания расщепится на две поляризованные по кругу компоненты, смещенные относительно ω₀ на величину ±Δω. В центре, где при Н = 0 находилась бы исследуемая спектральная линия, не будет наблюдаться никакого излучения.

Аналогично расщепляется линия поглощения при прохождении света сквозь исследуемое вещество в направлении линий напряженности внешнего магнитного поля. Это позволяет установить, как изменяется разность показателей преломления, определяющая угол вращения плоскости поляризации вблизи расщепленной в продольном магнитном поле линии поглощения. Проще всего провести такую оценку графически. Для этого воспользуемся графиком изменения показателя преломления вблизи линии поглощения. Сместив этот график вправо и влево на qН_внеш/(2тс), получим две дисперсионные кривые: А₁В₁С₁D₁ и А₂В₂С₂D₂ (рис.). Затем вычтем ординаты одной кривой из ординат другой и определим результирующую кривую, характеризующую изменение угла поворота плоскости поляризации вблизи линии поглощения.

В результате такого построения выявляются два интересных результата. Во-первых, в узком спектральном интервале вблизи линии поглощения дважды меняется знак эффекта Фарадея; угол вращения плоскости поляризации имеет один знак вне интервала ω₀±Δω и другой знак внутри этого интервала частот. Во-вторых угол вращения вблизи линии поглощения может быть очень большим, так как в исследуемой области происходит резкое изменение показателя преломления и коэффициента поглощения и разность (n_лев — n_пр) может принимать большие значения.

Опыт подтверждает выводы этой простой теории, и вращение плоскости поляризации парами металлов и другими веществами широко используется в современной атомной физике для определении атомных констант, а также для ряда других весьма тонких измерений.

Список использованной литературы.

Г.С. Ландсберг, Оптика – изд. 5-е, перераб. и доп. – М.: «Наука», 1976г.

Н.И. Калитиевский, Волновая оптика: Учеб. пособие для вузов. – 3-е изд., перераб. и доп. – М.: Высш. шк., 1995. – 463 с.: ил.

Date: 2016-07-25; view: 1316; Нарушение авторских прав