Тема лекции 3 Кручение прямого цилиндрического стержня.

Конспект лекции

1.4 Чистый сдвиг. Чистым сдвигом называется такой случай плос­кого напряженного состояния, при котором в окрест­ности данной точки можно выделить элементарный параллелепипед с боковыми гранями, находящимися под действием одних лишь касательных напряжений (рис. 1.10).

Определим нормальные и касательные напряжения на площадке п—п, про­ходящей через точку О и составляющей угол α с вертикальной исходной площадкой (рис. 1.10):

(1.4.1)

(1.4.2)

Из выражения (1.4.2) видно, что касательные напря­жения, показанные на рис. 1.10, по абсолютной вели­чине больше касательных напряжений по любым другим площадкам, проходящим через точку О (так как cos2 при и по абсолютной величине меньше единицы).

Следовательно, касательные напряжения , дей­ствующие по боковым граням рассматриваемого параллелепипеда, являются экстремальными ( и ), а эти грани являются площадками сдвига и образуют с главными площадками углы, равные 45°.

Эти площадки сдвига отличаются от площадок сдвига в общем случае напряженного состояния тем, что по ним не действуют нормальные напряжения. В связи с этим их называют площад­ками чистого сдвига.

Из формулы (1.4.1) следует, что при =45° имеет максималь­ное значение, равное τ = τ_max (так как при этом sin 2 = sin 90° = 1), a при =-45°—

минимальное зна­чение, равное τ = –τ_max. Следо­вательно, при чистом сдвиге глав–

Рисунок 1.10 ные напряжения (т. е. экстремальные нормальные напряжения) и экстре­мальные

касательные напряжения по абсолютной величине равны друг другу. Подставим в выражение (1.4.1) значения углов a₁ и α₂ = α₁ + 90^○ соответствующие двум взаимно перпен­дикулярным площадкам и получаем, что при чистом сдвиге нормальные напряжения на любых двух взаимно перпендикулярных площадках равны друг другу по величине и противопо­ложны по знаку. Поэтому чистым сдвигом можно называть такое плоское напряженное состояние, при котором нормальные

напряжения на двух взаимно перпендикулярных площадках равны друг другу по величине и противоположны по знаку.

Таким образом, напряженное состояние чистого сдвига можно изобразить в виде:

а) элементарного параллелепипеда, боковые грани которого совмещены с площадками чистого сдвига и по которым действуют только касательные напряже­ния τ_max и τ_min;

б) элементарного параллелепипеда с боковыми гранями, совпадающими с главными площадками, по которым действуют только нормальные напряжения σ_max= τ_max и ;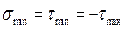

При чистом сдвиге полное напряжение р по любой площадке, как это следует из формул (1.4.1) и (1.4.2), равно по абсолютной величине напряже­нию τ_max.

Напряженное состояние, изображенное на рис 1.11, а, представляет собой чистый сдвиг. В этом состоянии длины ребер элементарного параллелепипеда не изменяются, а изменяются лишь углы между боковыми гранями: первоначально прямые углы становятся равными 90⁰ + и 90⁰- .

Каждая из граней параллелепипеда при деформации чистого сдвига перемещается относительно противоположной грани на величину АА' (рис.1.11, б), называемую абсолютным сдвигом. Отношение абсолютного сдвига к расстоянию между противополож­ными гранями называется относительным сдвигом, при малых деформациях оно равно углу сдвига —изменения первоначально прямых углов между боковыми гранями параллелепипеда. Абсолютный сдвиг выражается в мерах длины, а-относительный сдвиг является безразмерной величиной. Угол сдвига , как показывает опыт, прямо пропорционален касательным напряжениям. Эта зависимость между и , называемая законом Гука при сдвиге, выражается в виде

(1.4.3)

или

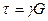(1.4.4)

Она справедлива при напряжениях, не превышающих предела пропорциональности материала.

Коэффициент пропорциональности G в формулах (1.4.3) и (1.4.4) называется модулем сдвига (или

модулем упругости второго рода).

Модуль сдвига является физической постоянной материала, характеризующей его жесткость (т. е. способность сопротивляться упругим деформациям) при сдвиге. Модуль сдвига G, как и модуль упругости Е, выражается в паскалях (Па), мегапаскалях (МПа) и т. д.

Деформации сдвига можно определять по фор­муле (1.4.3) не только при чистом сдвиге, но и в общем случае плоского напряженного состояния, когда по боковым граням параллелепипеда действуют не толь­ко касательные, но также и нормальные напряже­ния. Это является следствием того, что нормальные напряжения вызывают лишь поступательные переме­щения боковых граней параллелепипеда и не вызы­вают изменения его прямых углов.

1.5 Кручение прямого цилиндрического стержня. Кручение - это такой вид деформации бруса, при котором в его поперечных сечениях возникает единственный внутренний силовой фактор —

крутящий момент, обозначаемый М_к

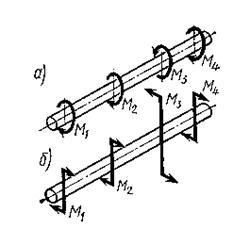Рисунок 1.12

1.5.1 Напряжения и деформации при кручении. Деформация кручения возникает при нагружении бруса па­рами сил, плоскости действия которых перпендикулярны его продольной оси. Моменты этих пар будем называть скручи­вающими моментами и обозначать М. На рис. 1.12, а изображен брус, работающий на кручение под действием приложенных к нему скручивающих моментов. Это условное

Рисунок 1.13

алгебраическая сумма скручивающих моментов равна нулю, т. е. брус находится в равновесии. На рис. 1.13, а,б изображен тот же брус в ортогональной проекции. При этом на рис. 1.13, а дан еще один способ условного изображения внешних моментов, часто при­меняемый в технической литературе; момент представлен в виде двух кружков. Кружок с точкой обозначает силу, направлен­ную на наблюдателя, а кружок с крестом - силу, направленную от наблюдателя.

Применяя метод сечений и рассматривая равновесие остав­ленной части (рис. 1.13, в, г), приходим к выводу, что внутренние силы, возникающие в поперечном сечении бруса, должны дать момент (крутящий момент), уравновешивающий внешние мо­менты, приложенные к оставленной части.

Итак, крутящий момент, возникающий в произвольном попе­речном сечении бруса, численно равен алгебраической сумме скручивающих моментов, приложенных к оставленной части.

При кручении бруса в его поперечных сечениях возникают только касательные напряжения. Для расчета на прочность, так же как и при растяжении (сжатии) бруса, надо найти его опасное сечение. В слу­чае, если размеры поперечного сечения по длине бруса по­стоянны, опасными будут сечения, в которых крутящий момент максимален. График, показывающий закон изменения крутя­щих моментов по длине бруса, называется эпюрой крутящих моментов. Построение этих эпюр принципиально ничем не от­личается от построения эпюр про­дольных сил и производится на основе сформулированного выше правила вычисления крутящих моментов. Для бруса, изображен­ного на рис. 1.13, а, б, эпюра М_к, представлена на рис. 1.13, д.

Знак крутящего момента не имеет физического смысла, но для определенности при построении эпюр условимся о следую­щем правиле знаков. Будем считать крутящий момент положи­тельным, если для наблюдателя, смотрящего на проведенное сечение, он представляется направленным по часовой стрелке. Соответствующий внешний момент направлен про­тив часовой стрелки.

Методами сопротивления материалов задача о напряжениях и перемещениях при круче­нии может

быть решена только для бруса круглого сплошного или кольцевого поперечного сечения.

Теория кручения бруса круглого поперечного сечения на­иболее часто используется при расчете различных валов. В ка­честве примера на рис. 1.14 показан так называемый трансмис­сионный вал с насаженными на него шкивами ременных передач.

Легко видеть, что под действием натяжений ремней вал по­мимо кручения испытывает и изгиб. Если пренебречь влиянием изгиба (так поступают при предварительном, ориентировочном расчете валов), расчетная схема вала будет иметь вид, пред­ставленный на рис. 1.15. Там же показана эпюра кру-

Рисунок 1.14 тящих мо­ментов.

При равномерном вращении вала алгебраическая сумма при­ложенных к нему вращающих моментов равна нулю.

Вращающие моменты, дей­ствующие на каждый из шкивов могут быть выражены через соответствующую мощность и угловую скорость по формуле, известной из курса теоретиче­ской механики:

М = Р/w, (1.5.1)

где М - момент, Нм; Р — мощность, Вт; w - угловая ско­рость, рад/с.

Вращающий момент может быть выражен также и через силы натяжения ветвей ремня. Например, для шкива I (рис. 1.14)

, (1.5.2)

где — диаметр шкива.

Для вычисления деформаций вала при кручении воспользу­емся формулой

dj = M dz / (GJ_p). (1.5.3)