Частотные критерии устойчивости [7, 8, 11].

Частотные методы исследования устойчивости основаны на связи расположения корней характеристического полинома (обозначим его функцией D(р) для любого типа систем) с годографом этого полинома на комплексной плоскости, т.е. с графиком комплексной функции D(jw) при изменении w от 0 до ∞. Это графоаналитические методы, позволяющие по виду частотных характеристик систем судить об их устойчивости. Их достоинство - в простой геометрической интерпретации, наглядности и в отсутствии ограничений на порядок дифференциального уравнения.

Принцип аргумента. Запишем характеристический полином в виде

D(p) = a₀ (p-p₁) (p-p₂)… (p-p_n) = 0,

Его корни: p_i = a_i + jw_i = |p_i| exp(j arg(p_i)), где arg(p_i) = arctg(w_i/a_i) + kp, |p_i| - значения модулей корней.

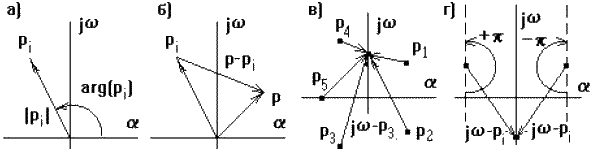Рис. 4.2.1.

Каждый корень можно изобразить вектором на комплексной плоскости (рис. 4.2.1а), тогда разность p - p_i изобразится разностью векторов (рис. 4.2.1б), где p - любое число.

Если изменять значение p произвольным образом, то конец вектора p - p_i будет перемещаться по комплексной плоскости, а его начало будет оставаться неподвижным, так как p_i - это конкретное неизменное значение. В частном случае, если на вход системы подавать гармонические колебания с различной частотой w, то p = jw, а характеристический полином принимает вид:

D(jw) = a₀ (jw - p₁) (jw - p₂)... (jw - p_n).

При этом концы векторов jw - p_i будут находиться на мнимой оси (рис. 4.2.1в). Если менять w от -∞ до +∞, то каждый вектор jw - p_i будет поворачиваться относительно своего начала p_i на угол +p для левых и -p для правых корней (рис. 4.2.1г).

Характеристический полином можно представить в виде

D(jw) = |D(jw)| exp(j arg(D(jw))),

где |D(jw)| = a₀ |jw-p₁| |jw-p₂|... |jw-p_n|, arg(D(jw)) = arg(jw-p₁) + arg(jw-p₂) +... + arg(jw-p_n).

Пусть из n корней m - правые, а n-m - левые, тогда угол поворота вектора D(jw) при изменении w от -∞ до ∞ равен

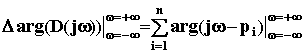= (n-m)p - mp,

или при изменении w от 0 до +∞:

= (n - 2m) (p/2). (4.2.1)

Отсюда вытекает правило: изменение аргумента вектора D при изменении частоты от -∞ до +∞ равно разности между числом левых и правых корней уравнения D(p) = 0, умноженному на p, а при изменении частоты от 0 до +∞ эта разность умножается на p/2.

Это и есть принцип аргумента. Он положен в основе всех частотных критериев устойчивости. Мы рассмотрим два наиболее распространенных критерия: критерий Михайлова и критерий Найквиста.

Критерий устойчивости Михайлова. Так как для устойчивой системы число правых корней m = 0, то угол поворота вектора D(jw) составит

= np/2. (4.2.2)

Рис. 4.2.2.

Система будет устойчива, если вектор D(jw) при изменении частоты от 0 до +∞ повернется на угол np/2. При этом конец вектора опишет кривую, называемую годографом Михайлова. Для построения годографа выражение (4.1.6) записывается с заменой p на jw в форме:

a₀pⁿ+a₁p^n-1+…+ a_n-1p+a_n = D(jw) = P(w) + jQ(w),

где P(w) - вещественная часть, как сумма всех членов характеристического уравнения, содержащих j в четных степенях, Q - мнимая часть выражения. Годограф начинается на положительной полуоси при D(0) = a_n, и, при изменении частоты от 0 до ∞, последовательно проходит против часовой стрелки n квадрантов комплексной плоскости, с уходом в бесконечность в n-ом квадранте (рис. 4.2.2а).

Если это правило нарушается (например, число проходимых кривой квадрантов не равно n, или нарушается последовательность прохождения квадрантов (рис. 4.2.2б)), то такая система неустойчива - это и есть необходимое и достаточное условие устойчивости по критерию Михайлова.

Критерий удобен своей наглядностью и используется, если известно уравнение замкнутой системы. Если кривая проходит вблизи начала координат, то система находится вблизи границы устойчивости и наоборот.

Рис. 4.2.3.

Критерий устойчивости Найквиста. Этот критерий основан на связи свойства устойчивости замкнутой системы с формой АФЧХ разомкнутой устойчивой системы. Разомкнутой системой являются все последовательно соединенные блоки от входа системы до точки замыкания обратной связи (рис. 4.2.3). Исследование разомкнутой системы проще, чем замкнутой, и его можно производить экспериментально.

Передаточная функция W_pc разомкнутой системы:

W_pс(jw) = K_pc(jw)/H_pc(jw),

с углом поворота фазы в соответствии с выражением (4.2.2):

D arg H_рс(jw) = np/2, 0 ≤ w ≤ ∞. (4.2.3)

АФЧХ замкнутой системы описывается выражением:

W_зс(jw)= W_pc(jw) /[1+ W_pc(jw)]. (4.2.4)

Обозначим знаменатель этого выражения через W₁(jw):

W₁(jw)=1+W_pc(jw)=1+K_pc(jw)/H_pc(jw)=H(jw)/H_pc(jw), (4.2.5)

где H(jw) = K_pc(jw) + H_pc(jw), характеристический полином замкнутой системы при р=jw.

В соответствии со свойствами передаточных функций порядок полинома Н(р) не превышает порядка полинома H_pc(p), т.к. H(p)=K_pc(p)+H_pc(p), а порядок полинома K_pc(p) меньше порядка полинома H_pc(p). Поэтому критерий Михайлова для замкнутой системы соответствует выражению:

D arg H(jw) = (n - 2m) (p/2), 0 ≤ w ≤ ∞. (4.2.6)

где m - число правых корней системы, имеющей в замкнутом состоянии характеристический полином Н(р)=0.

Из (4.2.5) следует:

D arg W₁(jw) = D arg H(jw) - D arg H_pc(jw).

C учетом (4.2.3):

D arg W₁(jw) = (n - 2m) (p/2) - np/2 = -mp. (4.2.7)

В устойчивой замкнутой системе правых корней в характеристическом уравнении нет, т. е. m=0, а, следовательно, условием устойчивости замкнутой системы будет:

D arg W₁(jw) = 0. (4.2.8)

Условие (4.2.8) выполняется только тогда, когда кривая W₁(jw) при изменении частоты от 0 до ∞ не охватывает начала координат комплексной плоскости. Действительно, только в этом случае результирующий поворот вектора W₁(jw) при изменении w от 0 до ∞ будет равен нулю, так как возрастание угла j(w), обусловленное движением вектора W₁(jw) в положительном направлении (против часовой стрелки), будет компенсироваться таким же убыванием j(w), обусловленным движением вектора W₁(jw) в отрицательном направлении (по часовой стрелке).

Как видно из (4.2.5), переход на комплексной плоскости от годографа вектора W₁(jw) к годографу вектора АФЧХ разомкнутой системы W_pс(jw) осуществляется сдвигом кривой W₁(jw) влево на -1, так как W_pc(jw) = W₁(jw) -1. С учетом этой операции, получаем следующую формулировку амплитудно-фазового критерия устойчивости Найквиста: линейная динамическая система, устойчивая в разомкнутом состоянии, устойчива и в замкнутом состоянии, если АФЧХ разомкнутой системы W_pс(jw) при изменении частоты от 0 до ∞ не охватывает на комплексной плоскости точку с координатами (-1; j0) (рис. 4.2.4, годограф 2).

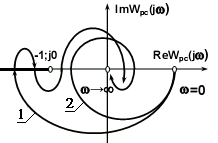Рис. 4.2.4.

Более общая формулировка критерия Найквиста относится к системам, имеющим так называемую АФЧХ второго рода (рис. 4.2.4, годограф 1), когда W_pс(jw) пересекает (неограниченное количество раз) вещественную ось левее точки Re W_pc(w) = -1. Будем считать положительным переход годографа через вещественную ось, если он совершается сверху вниз, и отрицательным, если он совершается снизу вверх. Для таких годографов критерий Найквиста формулируется в следующем виде: линейная динамическая система, устойчивая в разомкнутом состоянии, устойчива и в замкнутом состоянии, если при изменении частоты от 0 до +∞ разность между числом положительных переходов годографа АФЧХ разомкнутой системы через участок вещественной оси (-1; -∞) и числом отрицательных переходов равна нулю. Из этого условия видно, что система, устойчивая в разомкнутом состоянии и имеющая АФЧХ в форме кривой 1 на рис. 4.2.4, устойчива и в замкнутом состоянии.

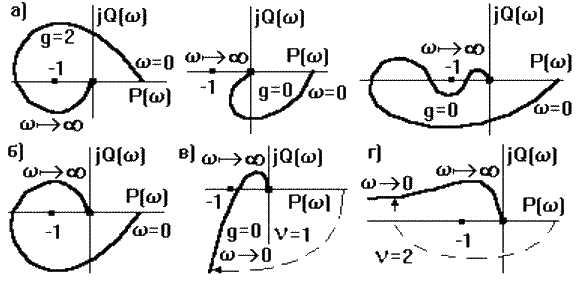Рис. 4.2.5.

На рис. 4.2.5а приведены АФЧХ разомкнутых САУ, устойчивых в замкнутом состоянии, на рис. 4.2.5б - замкнутая САУ неустойчива.

На рис. 4.2.5в и 4.2.5г показаны АФЧХ разомкнутых астатических САУ, соответственно устойчивых и неустойчивых в замкнутом состоянии. Их особенность в том, что АФЧХ при w ® 0 уходит в бесконечность. В этом случае при использовании критерия Найквиста ее мысленно замыкают на вещественную ось по дуге окружности бесконечно большого радиуса.

Критерий Найквиста нагляден. Он позволяет не только выявить, устойчива ли система, но и, в случае, если она неустойчива, наметить меры по достижению устойчивости.