Моделирование стандартных схем программ

1.4.1. Одноленточные автоматы

Конечный одноленточный (детерминированный, односторонний) автомат обнаруживают ряд полезных качеств, используемых в теории схем программ для установления разрешимости свойств ССП.

Одноленточный конечный автомат (ОКА) над алфавитом V задается набором

A = { V, Q, R, q₀, #, I } и правилом функционирования, общим для всех таких автоматов. В наборе А

V - алфавит;

Q - конечное непустое множество состояний (QÇV=Æ);

R - множество выделенных заключительных состояний (RÍQ);

q₀ - выделенное начальное состояние;

I - программа автомата;

# - «пустой» символ.

Программа автомата I представляет собой множество команд вида qа®q', в которой q,q'ÎQ, aÎV и для любой пары (q, a) существует единственная команда, начинающаяся этими символами.

Неформально ОКА можно представить как абстрактную машину, похожую на машину Тьюринга, но имеющую следующие особенности:

1) выделены заключительные состояния;

2) машина считывает символы с ленты, ничего не записывая на нее;

3) на каждом шаге головка автомата, считав символ с ленты и перейдя согласно программе в новое состояние, обязательно передвигается вправо на одну клетку;

4) автомат останавливается в том и только в том случае, когда головка достигнет конца слова, т.е. символа #.

Говорят, что автомат допускает слово a в алфавите V, если, начав работать с лентой, содержащей это слово, он останавливается в заключительном состоянии. Автомат A задает характеристическую функцию множества M_A допускаемых им слов в алфавите V, т. е. он распознает, принадлежит ли заданное слово множеству M_A если связать с остановкой в заключительном состоянии символ 1, а с остановкой в незаключительном состоянии – 0.

Наглядным способом задания ОКА служат графы автоматов. Автомат А представляется графом, множество вершин которого – множество состояний Q, и из вершины q в вершину q’ ведет дуга, помеченная символом а, тогда и только тогда, когда программа автомата содержит команду qа®q'. Работе автомата над заданным словом соответствует путь из начальной вершины q. Последовательность проходимых вершин этого пути – это последовательность принимаемых автоматом состояний, образ пути по дугам – читаемое слово. Любой путь в графе автомата, начинающийся в вершине q₀ и заканчивающийся в вершине q,ÎR, порождает слово, допустимое автоматом.

Пример 1.2. ОКА A = ({a, b}, {q₀, q₁, q₂, q₃}, {q₂}, q₀, #, I), допускающего слова {aⁿ b^m | n=1,2,...; m=1,2,...}, задается графом (рисунок 1.5). Программа I содержит команды:

q₀a®q₁; q₀b®q₃; q₁a®q₁; q₁b®q₂; q₂a®q₃; q₂b®q₂; q₃a®q₃; q₃b®q₃.

Автомат называется пустым, если М_А = Æ, Автоматы А1 и А2 эквивалентны, если М_А1 = М_А2. Для машины Тьюринга проблемы пустоты и эквивалентности неразрешимы, более того, они не являются частично разрешимыми. Ситуация меняется для конечных автоматов.

Для ОКА доказано:

1) Проблема пустоты ОКА разрешима.

Доказательство основано на проверке допустимости конечного множества всех слов, длина которых не превышает числа состояний ОКА - n. Если ни одно слово из этого множества не допускается, то ОКА «пуст».

2) Предположение о том, что минимальная длина допускаемого слова больше n отвергается на том основании, что оно может быть сведено к слову меньшей длины, путем выбрасывания участков между двумя повторяющимися в пути узлами.

3) Проблема эквивалентности ОКА разрешима.

Доказательство основано на использовании отношения эквивалентности двух состояний q и q': если состояния q и q' эквивалентны, то для всех aÎA состояния d(q, a) и d'(q', a) также эквивалентны. Формируемые пары не должны входить одновременно заключительное и незаключительное состояния.

1.4.2. Многоленточные автоматы

Многоленточный (детерминированный, односторонний) конечный автомат (МКА) задается так же, как ОКА. Отличие состоит в том, что множество состояний Q разбивается на n ³ 2 подмножеств (непересекающихся) Q₁,..., Q_n. «Физическая» интерпретация n - ленточного автомата отличается тем, что он имеет n лент и n головок, по головке на ленту. Если автомат находится в состоянии qÎQ_i, то i-я головка читает i-ю ленту так же, как это делает ОКА. При переходе МКА в состояние q'ÎQ_j (i¹j) i-я головка останавливается, а j-я начинает читать свою ленту. МКА останавливается, когда головка на одной из лент прочитает символ #.

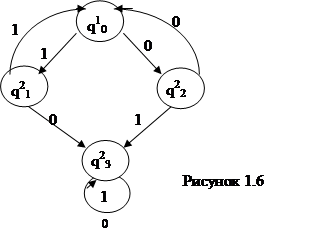Рассмотрим функционирование МКА с n=2 (рисунок 1.6) на примере сравнения пар слов в алфавите {1, 0} и допуске только совпадающих слов.

Здесь Q=Q₁UQ₂, где Q₁={q₀¹}; Q₂={q₁², q₂², q₃²}; R={q₀¹}; V={0, 1}, начальное состояние - q₀¹. МКА обрабатывает наборы слов (U₁, U₂), где слово U₁ записано на первой ленте, а U₂ - на второй. Допустимое множество наборов M_A -это все возможные пары одинаковых слов, т.е. наборы, где U₁ = U₂. Например, набор может быть (1101, 1101) и т.п.

В том случае, когда слова совпадают, МКА остановится в заключительном состоянии q₀¹ (именно в этом состоянии поступит символ #) и набор будет допущен. Если слова не совпадут хотя бы в одном символе, МКА перейдет в состояние q₃², из которого не выйдет до появления символа #, который и зафиксирует отсутствие совпадения слов, т.е. не допустит искаженный набор.

Доказывается разрешимость проблемы эквивалентности двухленточных автоматов.

1.4.3. Двухголовочные автоматы

Несмотря на то, что двухленточные и двухголовочные автоматы похожи друг на друга, их свойства сильно отличаются. Так, проблема пустоты разрешима для многоленточных автоматов и неразрешима для многоголовочных. Более того, в последнем случае она не является даже частично разрешимой. Проблема эквивалентности также не является частично разрешимой для многоголовочных автоматов. Однако проблема эквивалентности разрешима для двухленточных автоматов, и остается пока открытой для многоленточных автоматов с тремя и более лентами.

Двухголовочный конечный автомат (ДКА) имеет одну ленту и две головки, которые могут независимо перемещаться вдоль ленты в одном направлении. Множество состояний Q разбито на два непересекающихся множества. В состояниях Q₁ активна первая головка, а в состояниях Q₂ - вторая.

Двухголовочный автомат можно рассматривать как такой двухленточный автомат, который работает с идентичными словами на обеих лентах.

Приведем пример ДКА, который проверяет равенство двух последовательно записанных слов в алфавите V = {0, 1}. Признаком окончания каждого из слов сделаем вспомогательный символ *, не входящий в V. Автомат должен допускать только слова вида а * а *, где а Î V^*. Мы возьмем A = (V È {*}, Q₁ È Q₂, R, q₀¹, #, I), где Q₁ = {q₀¹, q₁¹, q₂¹, q₇¹} - множество состояний, в которых активна первая головка; Q₁ = {q₃², q₄², q₅², q₆²} - множество состояний, в которых активна вторая головка; R = { q₇¹} - множество, содержащее единственное заключительное состояние. Граф автомата показан на рисунке 1.7, на котором вместо многих «параллельных» дуг с разными

Рисунок 1.7. пометками нарисована одна дуга со всеми этими пометками.

Находясь в состоянии g₀¹, автомат передвигает первую головку к началу второго слова и, обнаружив его, переходит в состояние q₁¹. Если конец ленты # встречается раньше символа *, автомат переходит в незаключительное состояние q₆². Если же автомат приходит к состоянию q₁¹, он считывает поочередно символы второго слова первой головкой (состояние q₁¹), а символы первого слова — второй головкой (состояния q₃² и q₅²), сравнивая эти символы. Автомат возвращается каждый раз в состояние q₁¹, если символы одинаковы. Если же обнаружится несовпадение символов или первая головка встречает конец слова раньше символа *, автомат уходит в состояние q₆². Попав в это состояние, автомат не может выйти из него; перемещая вторую головку к концу слова на ленте, он достигает #, находясь в незаключительном состоянии, так что слово на ленте отвергается. Если первая головка достигнет конца второго слова, а вторая головка обнаружит, что первое слово тоже просмотрено до конца, то автомат перейдет в заключительное состояние q₇¹. В противном случае автомат перейдет в состояние q₆², отвергая слово.

Этот пример легко обобщить на случай произвольного алфавита V, увеличивая количество состояний множества Q.

Проблемы пустоты и эквивалентности.

Будем говорить, что ДКА моделирует работу машины Тьюринга над некоторым начальным словом, если автомат допускает единственное слово — конечный протокол paботы машины над ним.

Лемма (Розенберг). Существует алгоритм, который для любой машины Тьюринга и для любого начального слова строит двухголовочный автомат, моделирующий ее работу над этим словом.

Теорема. Проблема пустоты ДКА не является частично разрешимой.

Теорема. Проблема эквивалентности ДКА не является частично разрешимой.

Из неразрешимости проблемы пустоты немедленно следует неразрешимость проблемы эквивалентности, так как пустоту можно рассматривать как частный случай эквивалентности (например, эквивалентность фиксированному пустому автомату, пустой машине Тьюринга и т. д.). Если же проблема пустоты разрешима (частично разрешима), то проблема эквивалентности должна исследоваться независимо, так как в общем случае из разрешимости (частичной разрешимости) пустоты не следует разрешимость (частичная разрешимость) проблемы эквивалентности. Например, проблема пустоты разрешима для многоленточных автоматов, но проблема их эквивалентности открыта (для случая трех и более лент).

1.4.4. Двоичный двухголовочный автомат

Cтандартные схемы могут моделировать (в уточненном ниже смысле) двухголовочные автоматы, что позволяет свести проблему пустоты этих автоматов к проблеме пустоты схем. Такое моделирование можно осуществить более простым способом, если использовать специальный класс двухголовочных автоматов, а именно класс двоичных автоматов, работающих со словами над алфавитом {0, 1}. Следующая лемма устанавливает связь между классом всех двухголовочных автоматов и подклассом двоичных автоматов специального вида.

Лемма. Существует алгоритм преобразования двухголовочных автоматов в двоичные двухголовочные автоматы (ДДКА), сохраняющий пустоту автоматов (построенный двоичный автомат А_b пуст тогда и только тогда, когда пуст исходный автомат А).

Доказательство. Пусть ДКА А над алфавитом V = {a₁, a₂,...a_n} имеет множество состояний Q_А={q₁^k, q₂^k, …, q_k^k}, где верхний индекс (k = 1, 2) определяет номер активной головки. Преобразование этого автомата в двоичный начнем с кодировки символов и слов из V* словами в алфавите {0, 1} по следующему правилу:

код (#) = 0;

код (a_i) = 11....10 (i = 1, …, n);

код (aa_i) = код (a) код (a_i).

Так как символ # кодируется нулем, то любому непустому слову на ленте автомата А соответствует двоичное слово на ленте автомата А_b, оканчивающееся двумя нулями. Автомат останавливается, прочитав два нуля подряд (или 0, означающий пустое слово).

Автомат A преобразуется в двоичный автомат A_b так, как показано на графах рисунка 1.8. Каждый фрагмент графа А (рисунок 1.8, а) заменяется фрагментом (рисунок 1.8, б) для А_b.

После замены добавляются фрагменты (рисунок 1.8 в, г).

Множество состояний автомата А_b включает:

а) все старые состояния из Q_А;

б) для каждого старого состояния q_j^k n новых состояний, n - число символов алфавита V;

в) два новых состояния r₁¹ и r₂¹.

Заключительными состояниями автомата А являются заключительные состояния автомата А_b.

Вершины S_a (останов допускающий) и S_r (останов отвергающий) носят на графе вспомогательный характер в графе А_b.Они отмечают тот факт, что автомат прочитал два нуля подряд и остановился в заключительном состоянии (случай S_a) или в незаключительном состоянии (случай S_r).

Легко убедиться, что автомат А_ь допускает двоичное слово р тогда и только тогда, когда оно является двоичным кодом слова из V*, допускаемого автоматом А. Таким образом, из пустоты автомата А следует пустота автомата А_ь, и наоборот.

На рисунке 1.9, а приведен граф ДКА A допускающий только те слова в алфавите V = {a, b, c}, в которых символ a встречается не меньшее число раз, чем символы b и c, вместе взятые. Заключительное состояние R={q₀¹}. На рисунке 1.9, б приведен граф ДДКА, построенный по автомату А (10 – код символа a, 110 – код b, 1110 – код c).

По заданному ДДКА возможно построить ССП и наоборот, что позволяет решить задачу разрешимости (не разрешимости) свойств ССП, так как эта задача для ДДКА решена.

1.4.5. Построение схемы, моделирующей автомат

Двоичное слово b₁b₂ … b_n согласовано со свободной интерпретацией базиса B, если для любого i, 1£ i £ n, I(p) (‘fⁱa’) = b_i, где p - единственный предикатный символ базиса B.

Пример 1.3. Слово 101010100 согласовано с любой свободной интерпретацией I такой, что для всех i £ 9 I(p) (‘fⁱa’) = 1 если i нечетно и меньше 9, и I(p) (‘fⁱa’) = 0, если i четно или равно 9. Свободная интерпретация I такая, что для всех i I(p) (‘fia’) = 0, согласована с любым словом, не содержащим 1.

Для того чтобы свести проблему пустоты ДДКА к проблеме пустоты стандартных схем покажем, что для любого двоичного автомата А можно построить схему S, которая моделирует автомат А в следующем смысле. Если на ленту автомата А подано произвольное двоичное слово а, то программа (S, I), где I — любая свободная интерпретация базиса В, согласованная с а, останавливается в том и только в том случае, когда автомат допускает слово а.

Лемма. ДДКА пуст в том и только в том случае, если пуста моделирующая его стандартная схема.

Лемма. Для любого ДДКА можно построить моделирующую его стандартную схему.

Теорема (Лакхэм - Парк - Патерсон). Проблема пустоты, стандартных схем не является частично разрешимой.

Теорема (Лакхэм - Парк - Патерсон, Летичевекай). Проблема функциональной эквивалентности стандартных схем не является частично разрешимой.

Теорема (Лакхэм - Парк - Патерсон). Проблема тотальности стандартных схем частично разрешима.

Теорема (Патерсон). Проблема свободы, стандартных схем не является частично разрешимой.

Рекурсивные схемы

1.5.1. Рекурсивное программирование

Среди упомянутых выше методов формализации понятия вычислимой функции метод Тьюринга — Поста основан на уточнении понятия процесса вычислений, для чего используются абстрактные «машины», описанные в точных математических терминах. Другой подход (метод Черча — Клини) основан на понятии рекурсивной функции, рекурсивная функция задается с помощью рекурсивных определений. Рекурсивное определение позволяет связать искомое значение функции для заданных аргументов с известными значениями той же функции при некоторых других аргументах. Эта связь устанавливается с помощью универсального механизма рекурсии, дающего механическую процедуру поиска значений функции. Двум подходам к определению вычислимых функций соответствуют два метода программирования этих функций — операторное и рекурсивное программирование. При операторном методе программа представляет собой явно выписанную последовательность, описаний действий гипотетической вычислительной машины (последовательность операторов, команд и т. п.).

Язык Фортран — типичный представитель операторных языков. С другой стороны, рекурсивная программа — это совокупность рекурсивных определений, задающих рекурсивную функцию, для которой аргументами служат начальные данные программы, а значением — результат выполнения программы. Известный язык рекурсивного программирования — язык Лисп — предназначен для обработки символьной информации. В других зыках комбинируют оба метода программирования. Так, Паскаль — операторный язык с возможностью рекурсивного программирования, предоставляемой механизмом рекурсивных процедур и функций.

Примером рекурсивно определяемой функции является факториальная функция FACT: Nat → Nat:

FACT(х) = 1,если х = 0, FACT(х) = х ´ FACT(х — 1), если х > 0.

Операторные программы, вычисляющие значения этой функции, приведены в п. 1.1.3. Эту же функцию можно запрограммировать в некотором рекурсивном языке, базирующемся на механизме рекурсивных функций языка Паскаль:

FACT(a),

FACT(х) = if х = 0 then 1 else х ´ FACT(х - 1),

где а — некоторое целое неотрицательное число.

Выполнение этой программы для некоторого значения а(пусть а = 4) может быть осуществлено следующим образом. В обе части рекурсивного определения вместо хподставляется 4, после чего вычисляется правая часть определения. Вычисление правой части начинается с вычисления логического выражения. Если его значение 1 (истина), то вычисляется левое функциональное выражение (стоящее после то), а если его значение 0 (ложь) — вычисляется правое выражение (стоящее после else). Вычисление функционального выражения сводится к его упрощению, т. е. выполнению всех возможных вычислений. Если в упрощенном выражения остается вхождение символа определяемой функции FACT, то осуществляется переход к новому шагу выполнения программы. На этом шаге вхождение FACT(m), где m — значение внутри скобок после упрощения, заменяется левым ( т = 0) или правым ( m > 0) функциональным выражением, в котором все вхождения хзаменены на m. Упрощения продолжаются до тех пор, пока не будет получено выражение, не содержащее FACT(в нашем случае это выражение — число).

Вычисление рекурсивной программы может завершиться за конечное число шагов с результатом, равным значению запрограммированной функции для заданных аргументов (начальных значений переменных), но может и продолжаться бесконечно. В последнем случае значение функции не определено.

1.5.2. Определение рекурсивной схемы

Рекурсивная схема (РС) так же, как СПП определяется в некотором базисе. Полный базис РС, как и базис ССП, включает четыре счетных множества символов: переменные, функциональные символы, предикатные символы, специальные символы.

Множества переменных и предикатных символов ничем не отличаются от ССП. Множество специальных символов - другое, а именно: { if, то, else, (, ),, }. Отличие множества функциональных символов состоит в том, что оно разбито на два непересекающиеся подмножества: множество базовых функциональных символов и множество определяемых функциональных символов (обозначаются для отличия прописными буквами, например, F⁽¹⁾,G⁽²⁾, и т.д.).

В базисе РС нет множества операторов, вместо него – множество логических выражений и множество термов.

Простые термы определяются так же, как термы–выражения в СПП. Среди простых термов выделим базовые термы, которые не содержат определяемых функциональных символов, а также вызовы-термы вида F⁽ⁿ⁾(t₁,t₂,…t_n), где t₁,t₂,…t _n - простые термы, F⁽ⁿ⁾ - определяемый функциональный символ.

Логическое выражение - слово вида

p⁽ⁿ⁾(t₁,t₂,…t_n),

где p⁽ⁿ⁾ - предикатный символ, а t₁,t₂,…t_n - базовые термы.

Терм - это простой терм, или условный терм, т.е. слово вида if p then t₁ else t₂,

где p - логическое выражение, t₁, t₂ - простые термы, называемые левой и соответственно правой альтернативой.

Примеры термов:

− f(x, g(x, y)); h(h(a)) - базовые термы;

− f(F(x), g(x, F(y))); H(H(a)) - простые термы;

− F(x); H(H(a)) - вызовы;

− if p(x, y) then h(h(a)) else F(x) - условный терм.

Используется бесскобочная форма представления:

if pxy then hha else Fx - условный терм.

Расширим в базисе В множество специальных символов символом "=".

Рекурсивным уравнением, или определением функции F назовем слово вида

F⁽ⁿ⁾(x₁,x₂,…x_n) = t(x₁,x₂,…x_n),

где t(x₁,x₂,…x_n) - терм, содержащий переменные, называемые формальными параметрами функции F.

Рекурсивной схемойназывается пара (t, М), где t - терм, называемый главным термом схемы (или ее входом). М - такое множество рекурсивных уравнений, что все определяемые функциональные символы в левых частях уравнений различны и всякий определяемый символ, встречающийся в правой части некоторого уравнения или в главном терме схемы, входит в левую часть некоторого уравнения. Другими словами, в РС имеется определение всякой вызываемой в ней функции, причем ровно одно.

Примеры РС:

R_S1: F(x); F(x) = if p(x) then a else g(x, F(h(x))).

R_S2: A(b, c); A(x, y) = if p(x) then f(x) else B(x, y);

B(x, y) = if p(y) then A(g(x), a) else C(x, y);

C(x, y) = A(g(x), A(x, g(y))).

R_S3: F(x); F(x) = if p(x) then x else f(F(g(x)), F(h(x))).

Пара (R_S, I), где R_S - PC в базисе В, а I - интерпретация этого базиса, называется рекурсивной программой. При этом заметим, что определяемые функциональные символы не интерпретируются.

Протоколы выполнения программы (R_S1, I₁) и (R_S1, I₂), где I₁ и I₂ - интерпретации из п. 1.2.3 (рисунок 1.2, б, в), выглядят следующим образом: