Системы случайных величин

Случайные события

7. Случайным называется событие А, которое

А) может произойти, а может не произойти

Б) никогда не произойдет

В) обязательно произойдет

Г) произойдет только совместно с событием

8. События А и В называются зависимыми, если

А) сумма их вероятностей обязательно равна 1

Б) вероятности событий А и В не зависят друг от друга

В) вероятность наступления одного из событий зависит от появления или не появления другого

Г) они происходят одновременно

9. События А и В называются несовместными, если

А) вероятность наступления одного из событий зависит от появления или не появления другого

Б) появление одного из них исключает появление другого

В) сумма их вероятностей никогда не равна 1

Г) если одновременно они могут появиться только конечное число раз

10. Рассматривается пространство из N элементарных событий. Событию А благоприятствуют M элементарных событий. Классическая вероятность события А равна

А)

Б)

В)

Г)

11. Произведено n испытаний. Событие А произошло m раз. Относительная частота события А равна

А)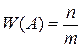

Б)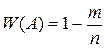

В)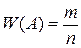

Г)

12. Вероятность любого события принадлежит отрезку

А) [1;2]

Б) [0;2]

В) [1;4]

Г) [0;1]

13. Сумма вероятностей событий, образующих полную группу, равна

А) 0

Б) 1/2

В) 1

Г) 4

14. Два события называются противоположными, если они

А) независимы

Б) не совместны

В) единственно возможны

Г) образуют полную группу событий

15. События образуют полную группу событий, если являются

А) независимыми

Б) единственно возможными и независимыми

В) несовместными и единственно возможными

Г) несовместными и равновозможными

16. Суммой событий А и В называется событие С,

которое происходит, если происходят:

А) только событие А

Б) только событие В

В) одно из событий А или В

Г) оба события А и В

17. Произведением событий А и В называется событие С,

которое происходит, если происходит:

А) только событие А

Б) только событие В

В) одно из событий А или В

Г) оба события А и В

18. Обязательным условием применения формулы

P(A + B)=P(A)+P(B)-P(AB)

является

А) независимость события А и В

Б) события А и В единственно возможны

В) события А и В противоположны

Г) совместность событий А и В

19. Обязательным условием применения формулы

P(A + B)=P(A)+P(B)

является

А) независимость события А и В

Б) несовместность событий А и В

В) события А и В единственно возможны

Г) совместность событий А и В

20. Вероятность P(A / B) это - …

А) вероятность события А при условии, что А и В противоположные события

Б) вероятность события А при условии, что А и В несовместные события

В) вероятность события А при условии, что событие В произошло

Г) произведение событий А и В

21. Обязательным условием применения формулы

P(AB)=P(A)P(B)

является

А) противоположность событий А и В

Б) независимость событий А и В

В) несовместность событий А и В

Г) зависимость событий А и В

22. Обязательным условием применения формулы

P(AB)=P(A)P()

является

А) противоположность событий А и В

Б) независимость событий А и В

В) несовместность событий А и В

Г) зависимость событий А и В

23. Формула полной вероятности имеет вид:

А)

Б)

В)

Г)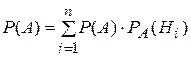

24. Вероятность появления события А m раз в n повторных независимых испытаниях при n <10 определяется

А) формулой Бернулли

Б) локальной теоремой Лапласа

В) интегральной теоремой Лапласа

Г) формулой Пуассона

25. Формула Бернулли имеет вид

А)

Б)

В)

Г)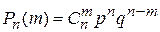

26. Наивероятнейшим числом наступлений события А в n независимых испытаниях называется

А) наибольшее число наступлений события А

Б) наибольшая вероятность наступления события А

В) число наступлений события А при наибольшем числе испытаний

Г) число наступлений события А, при котором вероятность наступления события А в n независимых испытаниях наибольшая

27. Формула для определения наивероятнейшего числа m ₀ имеет вид

А)

Б)

В)

Г)

28. Локальная теорема Лапласа позволяет вычислить

А) наивероятнейшее число наступлений события в n независимых испытаниях

Б) относительную частоту наступлений события в n независимых испытаниях

В) вероятность появления события m раз в n независимых испытаниях (n >10)

Г) вероятность отклонения числа появлений события m от числа независимых испытаний n

29. В локальной теореме Лапласа аргумент функции равен

А) В)

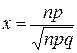Б) Г)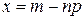

30. Интегральная теорема Лапласа позволяет вычислить

А) вероятность появления события A m раз в n испытаниях (n >10)

Б) вероятность появления события A в n испытаниях не менее а, но не более b раз (n >10)

В) наивероятнейшее число появлений события A в n независимых испытаниях (n >10)

Г) относительную частоту наступлений события A в n независимых испытаниях

31. В интегральной формуле Лапласа , аргумент равен

А)

Б)

В)

Г)

32. В интегральной формуле Лапласа , аргумент равен

А)

Б)

В)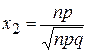

Г)

Случайные величины

33. Случайные величины делятся на

А) переменные и постоянные

Б) четные и нечетные

В) рациональные и нерациональные

Г) дискретные и непрерывные

34. Математическое ожидание дискретной случайной величины вычисляется по формуле

А)

Б)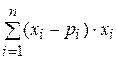

В)

Г)

35. Математическое ожидание случайной величины (с X+Y), где с =const, а X, Y - независимые случайные величины, равно:

А) c M(X)+M(Y)

Б) c M(X)-M(Y)

В) M(X)+M(Y)

Г)

36 Математическое ожидание постоянной величины С равно

А) С

Б) 1

В) 0

Г) не определено

37. Математическое ожидание произведения двух независимых случайных величин X и Y равно

А) M(X) + M(Y)

Б) M(X) - M(Y)

В)

Г)

38. Дисперсия дискретной случайной величины определяется по формуле:

А) В)

Б) Г)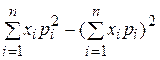

39. Дисперсия случайной величины (сX + Y), где c =const, а X, Y - независимые случайные величины, равно

А) c D(X)+D(Y)

Б) c ²D(X)+D(Y)

В) D(X)+D(Y)

Г) c D(X)-D(Y)

40. Дисперсия разности двух независимых случайных величин X и Y равна:

А) D (X)- D (Y)

Б) 0

В) D (X)+ D (Y)

Г)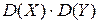

41. Дисперсия постоянной величины С равна

А) 1

Б) C

В) 0

Г) не определена

42. Математическое ожидание квадрата отклонения М (Х - М (Х))² равно

А) D (X)

Б) (Х)

В) M (X)

Г) V

43. Дисперсия от математического ожидания D (M (X)) равна

А) М (Х)

Б) 0

В) Х

Г) 1

44. Среднее квадратическое отклонение (х) случайной величины Х равно

А) D(X)

Б)

В)

Г) M(X)

45. Математическое ожидание M(X) непрерывной случайной величины X, заданной на интервале (a, b), определяется формулой:

А) M(x)= 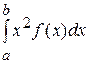В) M(x)=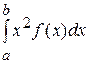

Б) M(x)= Г) M(x)=

46. Дисперсия D(X) непрерывной случайной величины, заданной на интервале (a, b), определяется формулой

А) D (X)= В) D (X)=

Б) D (X)= Г) D (X)=

47. Графическая форма задания закона распределения случайной величины - это

А) парабола

Б) прямая линия

В) окружность

Г) полигон

48. Табличная форма задания закона распределения случайной величины называется

А) суммой распределения

Б) интегралом распределения

В) рядом распределения

Г) полем распределения

49. Дискретная случайная величина принимает …:

А) только множество целых значений

Б) только множество положительных значений

В) все значения из интервала (-∞; +∞)

Г) конечное или бесконечное счетное множество значений

50. Непрерывная случайная величина принимает

А) множество целых значений

Б) множество рациональных значений

В) конечное множество значений

Г) любое значение из конечного или бесконечного интервала

51. Если X - непрерывная случайная величина, a и b - конкретные значения, то отсюда следует, что

А) Р(а≤Х<b) ≠ Р{а<Х≤b)

Б) Р(а<Х≤b) ≠ Р(а<Х<b)

В) Р(а<Х<b) ≠ Р(а≤Х≤b)

Г) Р(а≤X<b) = P(a≤X≤b) = P(a<X≤b) = P(a<X<b)

52. Если f (x) - плотность распределения, то равен

А) ∞

Б) -1

В) 0

Г) 1

53. Если f (x) - плотность распределения, то определяет

А) M(X)

Б) D(X)

В) (X)

Г) F(X)

54. Функция распределения случайной величины X задается формулой:

А)

Б)

В)

Г)

55. Дискретная случайная величина, выражающая число появления события А в n независимых испытаниях, проводимых в равных условиях и с одинаковой вероятностью появления события в каждом испытании, называется распределенной по …:

А) нормальному закону

Б) по закону Пуассона

В) биномиальному закону

Г) по показательному закону

56. Если случайная величина имеет биномиальное распределение, n - число независимых испытаний, а p - вероятность наступления события, то математическое ожидание вычисляется по формуле

А) M(X)= n

Б) M(X)= p

В) M(X)= npq

Г) M(X)= np

57. Если случайная величина имеет биномиальное распределение, n - число независимых испытаний, а p - вероятность наступления события, то дисперсия случайной величины вычисляется по формуле

А) D(X)= npq

Б) D(X) = np

В) D(X) = n-p

Г) D(X) = p

58. Математическое ожидание равномерно распределенной случайной величины вычисляется по формуле

А) M(X)=

Б) M(X)=

В) M(X)=

Г) M(X)= a + b

59. Дисперсия равномерно распределенной случайной величины вычисляется по формуле

А) D(X)=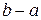

Б) D(X)=

В) D(X)=

Г) D(X)=

60. Вероятность попадания равномерно распределенной случайной величины в интервал [a,b] вычисляется по формуле:

А) P( ≤X≤ )=

Б) P( ≤X≤ )=

В) P( ≤X≤ )=

Г) P( ≤X≤ )=

61. Плотность распределения случайной величины с показательным распределением имеет вид:

А) f (x)= В) f (x)=

Б) f (x)= Г) f (x)=

62. Функция распределения случайной величины с показательным распределением имеет вид:

А) F (x)= В) F (x)=

Б) F (x)= Г) F (x)=

63. У показательного распределения математическое ожидание и среднее квадратическое отклонение

А) всегда различны

Б) всегда различаются на единицу

В) всегда равны

Г) всегда равны

64. Функция плотности нормального распределения с математическим ожиданием a и средне – квадратическим отклонением задается формулой:

А) В)

Б) Г)

65. График плотности нормального распределения называется

А) кривой Гаусса

Б) кривой Бернулли

В) кривой Пауссона

Г) кривой Лапласа

66. В точке x = a кривая Гаусса имеет

А) точку перегиба

Б) точку минимума

В) точку разрыва

Г) точку максимума

67. Точки и являются для кривой Гаусса

А) точками перегиба

Б) точками максимума

В) точками минимума

Г) точками разрыва

68. Параметрами нормального распределения являются:

А) математическое ожидание и среднеквадратическое отклонение

Б) функция распределения и функция плотности распределения

В) функция р (х) и Ф (х)

Г) дисперсия и среднеквадратическое отклонение

Системы случайных величин

69. Условная вероятность того, что случайная величина Y примет значение при условии, что определяется равенством

А)

Б)

В)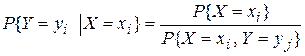

70. Дисперсией дискретной системы с.в. (X, Y) называется совокупность двух дисперсией DX и DY, определяемых равенствами

А)

Б)

В)

71. Дисперсией непрерывной системы с.в. (X, Y) называется совокупность двух дисперсией DX и DY, определяемых равенствами

А)

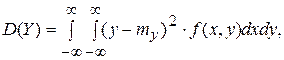
Б)

В)

72. Если (X, Y) – дискретная двумерная случайная величина, то корреляционный момент вычисляется по формуле

А) ,

Б)

В)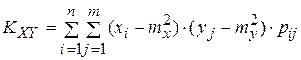

73. Если (X, Y) –непрерывная двумерная случайная величина, то корреляционный момент вычисляется по формуле

А)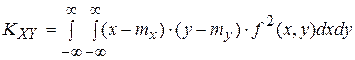

Б) ,

В)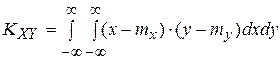

74. Если (X, Y) –непрерывная двумерная случайная величина, то корреляционный момент вычисляется по формуле

А)

Б)

В)

75. Коэффициент корреляции двух с.в. Х и У вычисляется по формуле

А)

Б)

В)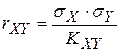

«Математическая статистика»

76. Генеральная совокупность – это …

А) вся исследуемая совокупность объектов

Б) совокупность случайно отобранных объектов

В) совокупность объектов, выбранных через определенный интервал

Г) совокупность из непересекающихся групп

77. Выборочная совокупность – это …

А) совокупность из непересекающихся групп

Б) совокупность случайно отобранных объектов

В) вся исследуемая совокупность объектов

Г) совокупность объектов, выбранных через определенный интервал

78. Объем выборки – это …

А) число, равное количеству объектов генеральной или выборочной совокупности

Б) число, равное среднему арифметическому объектов

В) число, равное максимальному значению совокупности

Г) число, равное минимальному значению совокупности

79. При повторном отборе зарегистрированные и обследованные единицы

А) вновь возвращаются в генеральную совокупность и снова могут принять участие в дальнейшем отборе

Б) в генеральную совокупность не возвращаются

В) в генеральную совокупность возвращаются, но принять участие в дальнейшем отборе не могут

Г) помечаются специальным знаком

80. При бесповторном отборе зарегистрированные и обследованные единицы

А) возвращаются в генеральную совокупность

Б) не возвращаются в генеральную совокупность

В) возвращаются в генеральную совокупность и могут принять участие в дальнейшем отборе

Г) либо возвращаются, либо не возвращаются в генеральную совокупность

81. Графическая форма задания закона распределения случайной величины - это

А) парабола

Б) прямая линия

В) окружность

Г) полигон

82. … – это наиболее часто встречающееся значение варианты.

А) медиана

Б) мода

В) размах варьирования

Г) среднее значение

83. … – это варианта, которая делит вариационный ряд на две равные части

А) медиана

Б) мода

В) размах варьирования

Г) среднее значение

84. … – это разность между наибольшей и наименьшей вариантой

А) медиана

Б) мода

В) размах варьирования

Г) среднее значение

85. Формула Стерджесса имеет вид …

А)

Б)

В)

Г)

86. Выборочная средняя вычисляется по формуле

А)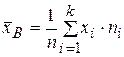

Б)

В)

87. Выборочная дисперсия вычисляется по формуле

А)

Б)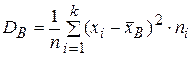

В)

88. Исправленная выборочная дисперсия вычисляется по формуле

А)

Б)

В)

89. Величина, характеризующая степень несимметричности рассеяния значений по одну и по другую сторону от средней называется …

А) эксцесс

Б) асимметрия

В) коэффициент изменчивости

Г) среднее квадратическое отклонение

90. … – это величина распределения выборки, которая характеризует остроту вершины полигона или гистограммы

А) эксцесс

Б) асимметрия

В) коэффициент изменчивости

Г) среднее квадратическое отклонение

91. Доверительный интервал – это интервал, в который с надежностью попадает

А) характеристика генеральной совокупности

Б) характеристика выборочной совокупности

В) значение изучаемого признака генеральной совокупности

Г) значение изучаемого признака выборочной совокупности

92. Надежностью оценки числовой характеристики генеральной совокупности называется

А) вероятность попадания этой характеристики в доверительный интервал

Б) отношение предельной ошибки выборки к средней ошибке

В) доверительный интервал

Г) точность оценки

93. Доверительный интервал для математического ожидания при известной дисперсии имеет вид

А)

Б)

В)

94. Доверительный интервал для математического ожидания при неизвестной дисперсии имеет вид

А)

Б)

В)

95. Статистические гипотезы

А) выдвигаются о выборочных совокупностях, а проверяются по генеральным совокупностям

Б) выдвигаются о выборочных совокупностях, а проверяются тоже по выборочным совокупностям

В) выдвигаются о генеральных совокупностях, а проверяются по выборочным совокупностям

Г) выдвигаются о генеральных совокупностях, а проверяются тоже по генеральным совокупностям

96. Проверяемая гипотеза обозначается

А) Н ₀

Б) H ₂

В) H ₁

Г) H ₃

97. Альтернативная (конкурирующая) обозначается через

А) H ₀

Б) H ₂

В) H ₃

Г) H ₁

98. При статистической проверке гипотез критические точки это

А) множество точек, образующих область принятия H ₀

Б) множество точек, образующих область принятия H ₁

В) точки, разделяющие область принятия гипотезы H₀ и область отвергания H ₀

Г) область существования H ₀

99. Множество всех значений критерия, при которых H ₀ отвергается, называется

А) областью определения

Б) областью принятия гипотезы

В) критической областью

Г) областью существования

100. Ошибка первого рода состоит в том, что

А) отвергается нулевая гипотеза , когда на самом деле она верна

Б) отвергается альтернативная гипотеза , когда на самом деле она верна

101. Ошибка второго рода состоит в том, что

А) отвергается нулевая гипотеза , когда на самом деле она верна

Б) отвергается альтернативная гипотеза , когда на самом деле она верна

102. При статистической проверке гипотез уровнем значимости 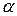называется:

А) вероятность допустить ошибку 1 – ого рода, т.е. принять правильную нулевую гипотезу

Б) вероятность допустить ошибку 1 – ого рода, т.е. отвергнуть правильную нулевую гипотезу

В) вероятность допустить ошибку 2 – ого рода, т.е. отвергнуть правильную нулевую гипотезу

Г) вероятность допустить ошибку 2 – ого рода, т.е. принять неправильную нулевую гипотезу

103. При статистической проверке гипотез мощностью критерия называют величину , то есть:

А) вероятность допустить ошибку 1 – ого рода, т.е. принять правильную нулевую гипотезу

Б) вероятность допустить ошибку 1 – ого рода, т.е. отвергнуть неправильную нулевую гипотезу

В) вероятность недопущения ошибки 2 – ого рода, т.е. отвергнуть правильную нулевую гипотезу

Г) вероятность допущения ошибку 2 – ого рода, т.е. принять неправильную нулевую гипотезу

104. Формула для вычисления 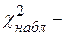выборочного значения статистики критерия имеет вид

А)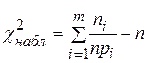

Б)

В)

105. Выборочный коэффициент корреляции вычисляется по формуле

А)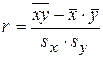

Б)

В)

106. Коэффициент корреляции принимает значения

А) от 0 до 1

Б) от -∞ до +∞

В) от 0 до +∞

Г) от -1 до 1

107. Если коэффициент корреляции равен 0, то … между признаками

А) существует положительная связь

Б) существует отрицательная связь

В) линейная связь отсутствует

Г) линейная связь присутствует

108. Корреляционная зависимость – это зависимость, проявляющаяся в том, что…

А) изменение одной из величин приводит к строго определенному изменению другой величины

Б) изменение одной из величин влечет изменение среднего значения другой

В) изменение одной из величин приводит к изменению другой величины в 2 раза

Г) изменение одной из величин влечет изменение другой в 2 раза

109. Выборочное уравнение прямой линии регрессии Y на X имеет вид

А)

Б)

В)

Г)

110. Выборочное уравнение прямой линии регрессии X на Y имеет вид

А)

Б)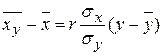

В)

Г)

Date: 2016-07-25; view: 268; Нарушение авторских прав