
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Пример решения транспортной задачи
|
|
Проиллюстрируем ход решения транспортной задачи на конкретном примере.
Пример. Решить транспортную задачу, определяемую следующей матрицей тарифов (табл. 3).
Таблица 3
| Потребители | Накопленный запас груза | ||||
| В 1 | В 2 | В 3 | |||
| Поставщики | А 1 | ||||
| А 2 | |||||
| А 3 | |||||
| Спрос |
Решение
1. Вычислим и сравним совокупные запасы груза у поставщиков и совокупный спрос потребителей: совокупные запасы груза 50 + 80 + 90 = 220,
а совокупный спрос 50 + 50 + 100 = 200. Таким образом, совокупные запасы больше совокупного спроса на 20 единиц. Чтобы их уравнять, нужно ввести фиктивного потребителя В 4 со спросом 20 единиц. Тарифы перевозок, связанных с фиктивным потребителем, примем равными нулю.
2. Построим распределительную таблицу (табл. 4). В правых верхних углах ее клеток запишем соответствующие тарифы перевозок.
Таблица 4
| Потребители | Накопленный запас груза | |||||
| В 1 | В 2 | В 3 | В 4 | |||
| Поставщики | А 1 | 1 | 7 | 2 | 0 | |
| А 2 | 3 | 11 | 5 | 0 | ||
| А 3 | 4 | 10 | 8 | 0 | ||
| Спрос |
3. Построим начальный план перевозок методом северо-западного угла. Загрузку табл. 4 начнем с клетки (1; 1), соответствующей поставщику А 1 с запасом груза 50 единиц и потребителю В 1 со спросом 50 единиц. Как видим, спрос и предложение совпали, поэтому данную клетку загрузим числом 50 (минимальным из двух чисел: 50 единиц запаса груза и 50 единиц спроса). Сравним теперь сумму 50 загрузок клеток в первой графе табл. 4
(в ней находится только что загруженная клетка (1; 1)) со спросом 50 в этой графе и увидим, что эта сумма не меньше соответствующего спроса (равна ему). Следовательно, следующая загружаемая клетка находится справа от только что загруженной клетки (1; 1) – это клетка (1; 2), соответствующая поставщику А 1 с остатком запаса груза 50 – 50 = 0 и потребителю В 1 со спросом 50. Минимальным из этих чисел (0) загрузим клетку
(1; 2) и определим следующую загружаемую клетку (табл. 5, 6).
Таблица 5
| Потребители | Накопленный запас груза | |||||
| В 1 | В 2 | В 3 | В 4 | |||
| Поставщики | А 1 | 1 | 7 | 2 | 0 | |
| А 2 | 3 | 11 | 5 | 0 | ||
| А 3 | 4 | 10 | 8 | 0 | ||
| Спрос |
Таблица 6
| Потребители | Накопленный запас груза | |||||
| В 1 | В 2 | В 3 | В 4 | |||
| Поставщики | А 1 | 1 | 7 | 2 | 0 | |
| А 2 | 3 | 11 | 5 | 0 | ||
| А 3 | 4 | 10 | 8 | 0 | ||
| Спрос |
Сравним сумму 0 загрузок клеток во второй графе (в ней находится только что загруженная клетка (1; 2)) со спросом 50 в данной графе и увидим, что данная сумма меньше соответствующего спроса. Следовательно, загружаемая клетка находится ниже только что загруженной клетки (1; 2) – это клетка (2; 2), соответствующая поставщику А 2 с запасом груза 80 единиц и потребителю В 2 с остатком спроса 50 – 0 = 50 единиц. Минимальным из этих чисел (50) загрузим клетку (2; 2). Сравним сумму 0 + 50 = 50 загрузок клеток второй графы, в которой находится только что загруженная клетка (2; 2), со спросом 50 в данной графе, увидим, что эта сумма не меньше соответствующего спроса (равна ему). Следовательно, загружаемая клетка находится справа от только что загруженной клетки (2; 2) – это клетка (2; 3), соответствующая поставщику А 2 с остатком запаса груза
80 – 50 = 30 единиц и потребителю В 3 со спросом 100 единиц. Минимальным из данных чисел (30) загрузим клетку (2; 3). Мы увидим, что сумма 30 загрузок всех клеток третьей графы, в которой находится только что загруженная клетка (2; 3), меньше спроса 100 в этой графе. Далее будем загружать клетку ниже только что загруженной клетки (2; 3), т. е. клетку
(3; 3), соответствующую поставщику А 3 с запасом груза 90 и потребителю В 3 с остатком спроса 100 – 30 = 70.
Минимальным из этих чисел (70) загрузим данную клетку. Так как сумма 30 + 70 = 100 загрузок всех клеток третьей графы, в которой находится только что загруженная клетка (3; 3), не меньше спроса 100 в этой графе (равна ей), то далее будем загружать клетку справа от клетки (3; 3), т. е. клетку (3; 4), соответствующую поставщику А 3 с остатком запаса груза 90 – 70 = 20 и потребителю В 4 со спросом 20. Следовательно, клетку (3; 4) загрузим числом 20, и на этом, очевидно, построение начального плана перевозок завершится (табл. 7).
Таблица 7
| Потребители | Накопленный запас груза | |||||
| В 1 | В 2 | В 3 | В 4 | |||
| Поставщики | А 1 | 1 | 7 | 2 | 0 | |
| А 2 | 3 | 11 | 5 30 | 0 | ||
| А 3 | 4 | 10 | 8 70 | 0 20 | ||
| Спрос |
Убедимся, что начальный план перевозок построен правильно. Для этого достаточно увидеть, что количество загруженных клеток равно  , сумма загрузок в каждой строке равна соответствующему запасу груза, а сумма загрузок в каждой графе равна соответствующему спросу.
, сумма загрузок в каждой строке равна соответствующему запасу груза, а сумма загрузок в каждой графе равна соответствующему спросу.
4. Для каждого поставщика  и каждого потребителя
и каждого потребителя 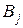 найдем потенциалы
найдем потенциалы  и
и  соответственно. Для этого решим составленную по определенным правилам систему линейных алгебраических уравнений. Первое уравнение данной системы имеет вид:
соответственно. Для этого решим составленную по определенным правилам систему линейных алгебраических уравнений. Первое уравнение данной системы имеет вид:  . Остальные уравнения составим по загруженным клеткам. По загруженной клетке (1; 1) с тарифом перевозок 1 (см. табл. 4) получается уравнение
. Остальные уравнения составим по загруженным клеткам. По загруженной клетке (1; 1) с тарифом перевозок 1 (см. табл. 4) получается уравнение  ; по загруженной клетке (1; 2) с тарифом перевозок 7 получаем уравнение
; по загруженной клетке (1; 2) с тарифом перевозок 7 получаем уравнение  ; аналогично по остальным загруженным клеткам: (2; 2) с тарифом 11, (2; 3) с тарифом 5, (3; 3) с тарифом 8 и, наконец, (3; 4) с тарифом 0 получаем соответственно уравнения
; аналогично по остальным загруженным клеткам: (2; 2) с тарифом 11, (2; 3) с тарифом 5, (3; 3) с тарифом 8 и, наконец, (3; 4) с тарифом 0 получаем соответственно уравнения  ,
,  ,
,  ,
,  .
.
Решая систему этих уравнений методом подстановки, получим:  ,
, 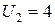 ,
, 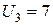 ,
,  ,
,  ,
, 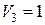 ,
,  . Найденные значения потенциалов
. Найденные значения потенциалов  и
и  удобно записать в распределительной таблице (табл. 8).
удобно записать в распределительной таблице (табл. 8).
Таблица 8
| Потребители | Накопленный запас груза | ||||||
| В 1 | В 2 | В 3 | В 4 | Ui | |||
| Поставщики | А 1 | 1 | 7 0 | 2 | 0 | ||
| А 2 | 3 | 11 50 | 5 | 0 | |||
| А 3 | 4 | 10 | 8 70 | 0 20 | |||
| Спрос | |||||||
| Vj | –7 |
5. Для каждой незагруженной клетки (i; j) вычислим разность 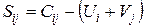 . В нашей распределительной таблице (см. табл. 8) не загружены клетки (1; 3), (1; 4), (2; 1), (2; 4), (3; 1) и (3; 2). Соответствующие им разности равны:
. В нашей распределительной таблице (см. табл. 8) не загружены клетки (1; 3), (1; 4), (2; 1), (2; 4), (3; 1) и (3; 2). Соответствующие им разности равны:
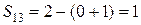 ;
;
 ;
;
 ;
;
 ;
;
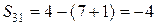 ;
;
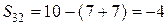 .
.
Как видим, среди этих разностей  есть отрицательные:
есть отрицательные:  ,
,  ,
, 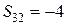 . Выберем из них максимальную по модулю, чтобы в соответствующей клетке поставить знак «+». Очевидно, что таких у нас две:
. Выберем из них максимальную по модулю, чтобы в соответствующей клетке поставить знак «+». Очевидно, что таких у нас две:  , соответствующая клетке (3; 1) с тарифом 4, и
, соответствующая клетке (3; 1) с тарифом 4, и 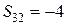 , соответствующая клетке (3; 2) с тарифом 10. Знак «+» поставим в той из этих клеток, в которой записан меньший тариф, т. е. в клетке (3; 1) (табл. 9).
, соответствующая клетке (3; 2) с тарифом 10. Знак «+» поставим в той из этих клеток, в которой записан меньший тариф, т. е. в клетке (3; 1) (табл. 9).
Таблица 9
| Потребители | Накопленный запас груза | ||||||
| В 1 | В 2 | В 3 | В 4 | Ui | |||
| Поставщики | А 1 | 1 | 7 0 | 2 | 0 | ||
| А 2 | 3 | 11 50 | 5 | 0 | |||
| А 3 | 4 + | 10 | 8 70 | 0 20 | |||
| Спрос | |||||||
| Vj | –7 |
6. Строим замкнутый контур по правилам, указанным в алгоритме метода потенциалов. Для этого из клетки (3; 1), помеченной знаком «+», «пойдем» по вертикали в загруженную клетку (1; 1); затем «пойдем» по горизонтали в загруженную клетку (1; 2), затем – по вертикали в загруженную клетку (2; 2), затем – по горизонтали в загруженную клетку (2; 3), затем – по вертикали в загруженную клетку (3; 3) и, наконец, по горизонтали вернемся в клетку (3; 1), помеченную знаком «+» (табл. 10).
Таблица 10
| Потребители | Накопленный запас груза | ||||||
| В 1 | В 2 | В 3 | В 4 | Ui | |||
| Поставщики | А 1 |  1 1
| 7 0 | 2 | 0 | ||
| А 2 | 3 | 11 50 | 5 | 0 | |||
| А 3 | 4 + | 10 | 8 70 | 0 20 | |||
| Спрос | |||||||
| Vj | –7 |
7. Обходя построенный замкнутый контур, например, по часовой стрелке, ставим в его углах поочередно знаки «–» и «+», учитывая, что в клетке (3; 1) уже стоит знак «+» (табл. 11).
Таблица 11
| Потребители | Накопленный запас груза | ||||||
| В 1 | В 2 | В 3 | В 4 | Ui | |||
| Поставщики | А 1 |  – 1 – 1
| + 7 0 | 2 | 0 | ||
| А 2 | 3 | –11 50 | + 5 | 0 | |||
| А 3 | 4 + | 10 | 8 70 – | 0 20 | |||
| Спрос | |||||||
| Vj | –7 |
8. Строим следующую распределительную таблицу, в которую без изменения перенесем из предыдущей таблицы, во-первых, все тарифы перевозок и, во-вторых, загрузки всех клеток, не помеченных знаками «+» и «–». Отметим, что во всех последующих распределительных таблицах можно не указывать запас груза, накопленный у поставщиков, а также спрос в пунктах потребления (табл. 12).
Обратите внимание на то, что в предыдущей таблице только одна загруженная клетка не была помечена знаками «+» и «–» – это клетка (3; 4);
в следующую таблицу мы перенесли без изменения загрузку 20 только данной клетки. Для вычисления новых загрузок клеток со знаками «+» и «–» рассмотрим загрузки клеток, помеченных знаком «–» в предыдущей таблице (загрузка 50 в клетке (1; 1), загрузка 50 в клетке (2; 2) и загрузка 70 в клетке (3; 3)), и среди данных загрузок выберем минимальную, т. е. 50. Ее в клетках со знаком «–» отнимем, а в клетках со знаком «+» прибавляем к имеющимся там загрузкам. Отметим, что в клетках (1; 1) и (2; 2) при вычитании получится нулевая загрузка. Следовательно, в одной из клеток мы нулевую загрузку в новой таблице писать не будем, а именно в клетке (2; 2), так как тариф клетки 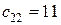 больше тарифа клетки (1; 1)
больше тарифа клетки (1; 1) 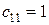 . В результате получим следующий (улучшенный) план перевозок (табл. 13).
. В результате получим следующий (улучшенный) план перевозок (табл. 13).
Таблица 12 Таблица 13
| Потребители | |||||
| В 1 | В 2 | В 3 | В 4 | ||
| Поставщики | А 1 | 1 | 7 | 2 | 0 |
| А 2 | 3 | 11 | 5 | 0 | |
| А 3 | 4 | 10 | 8 | 0 |
| Потребители | |||||
| В 1 | В 2 | В 3 | В 4 | ||
| Поставщики | А 1 | 1 | 7 | 2 | 0 |
| А 2 | 3 | 11 | 5 | 0 | |
| А 3 | 4 | 10 | 8 | 0 |
Для контроля правильности преобразования распределительной таблицы убедимся, что в новой таблице загруженных клеток столько же, сколько их было в предыдущей таблице – ровно 6.
9. Уже для новой распределительной таблицы находим потенциалы  и
и  всех поставщиков и потребителей. С этой целью решим систему линейных алгебраических уравнений:
всех поставщиков и потребителей. С этой целью решим систему линейных алгебраических уравнений:

составленную, во-первых, из уравнения  и, во-вторых, из уравнений
и, во-вторых, из уравнений 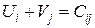 для загруженных клеток: (1; 1) с тарифом 1, (1; 2) с тарифом 7, (2; 3) с тарифом 5, (3; 1) с тарифом 4, (3; 3) с тарифом 8 и (3; 4) с тарифом 0. Значения потенциалов
для загруженных клеток: (1; 1) с тарифом 1, (1; 2) с тарифом 7, (2; 3) с тарифом 5, (3; 1) с тарифом 4, (3; 3) с тарифом 8 и (3; 4) с тарифом 0. Значения потенциалов  и
и  , являющиеся решением этой системы, запишем в распределительную таблицу (табл. 14).
, являющиеся решением этой системы, запишем в распределительную таблицу (табл. 14).
Таблица 14
| Потребители | Ui | |||||
| В 1 | В 2 | В 3 | В 4 | |||
| Поставщики | А 1 | 1 | 7 | 2 | 0 | |
| А 2 | 3 | 11 | 5 | 0 | ||
| А 3 | 4 | 10 | 8 | 0 20 | ||
| Vj | –3 |
10. Для каждой незагруженной клетки (i; j) вычислим разность 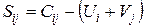 :
:
 ;
;
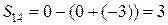 ;
;
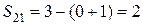 ;
;
 ;
;
 ;
;
 .
.
Отметим, что среди этих разностей  есть одна отрицательная –
есть одна отрицательная – 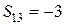 ; следовательно, в соответствующей клетке (1; 3) поставим знак «+». Затем построим замкнутый контур по указанным выше правилам; обходя данный контур, например, по часовой стрелке, поставим в его углах поочередно знаки «–» и «+» (табл. 15).
; следовательно, в соответствующей клетке (1; 3) поставим знак «+». Затем построим замкнутый контур по указанным выше правилам; обходя данный контур, например, по часовой стрелке, поставим в его углах поочередно знаки «–» и «+» (табл. 15).
Обратите особое внимание на следующие обстоятельства:
а) при построении замкнутого контура нам пришлось «пройти», не «поворачивая», через загруженные клетки (1; 2) и (2; 3), а также через незагруженные клетки (2; 1) и (3; 2); напомним, что указанными выше правилами это не возбраняется; нам было важно «поворачивать» каждый раз в загруженной клетке и «вернуться» в клетку (1; 3), из которой начали «движение»;
б) знаками «–» и «+» отмечены только угловые клетки построенного контура; «транзитные» клетки (как загруженные (1; 2), (2; 3), так и незагруженные (2; 1), (3, 2)) знаками «–» и «+» не отмечаются;
в) мы не стремимся к тому, чтобы замкнутый контур охватил все загруженные клетки – через загруженную клетку (3; 4), как видим, построенный замкнутый контур не проходит.
Таблица 15
| Потребители | Ui | |||||
| В 1 | В 2 | В 3 | В 4 | |||
| Поставщики | А 1 |  – 1 – 1
| 7 | 2 + | 0 | |
| А 2 | 3 | 11 | 5 | 0 | ||
| А 3 | 4 50 + | 10 | 8 20 – | 0 20 | ||
| Vj | –3 |
11. Построим следующую распределительную таблицу, в которую перенесем без изменений из предыдущей таблицы, во-первых, тарифы перевозок, во-вторых, загрузки 50, 80, 20 клеток (1; 2), (2; 3), (3; 4), не помеченных знаками «+» и «–» (табл. 16).
Таблица 16
| Потребители | |||||
| В 1 | В 2 | В 3 | В 4 | ||
| Поставщики | А 1 | 1 | 7 | 2 | 0 |
| А 2 | 3 | 11 | 5 | 0 | |
| А 3 | 4 | 10 | 8 | 0 |
Вычислим новые загрузки клеток, помеченных в предыдущей таблице знаками «+» и «–». Для этого, как обычно, среди загрузок 0 и 20 клеток (1; 1) и (3; 3), помеченных знаками «–» (см. табл. 15), выберем минимальную, т. е. 0. Эту минимальную загрузку 0 теперь нужно в клетках со знаком «–» отнять,
а в клетках со знаком «+» прибавить к имеющимся там загрузкам.
Поскольку в данном случае отнимается и прибавляется ноль, то на первый взгляд кажется, что в результате этих операций распределительная таблица не изменяется. Однако при строгом следовании изложенному выше алгоритму убедимся, что изменения в таблице все-таки происходят: во-первых, в незагруженной ранее клетке (1; 3) появится нулевая загрузка; во-вторых, в новой таблице в клетке (1; 1) нулевую загрузку, получающуюся при вычитании (об этом свидетельствует знак «–» в этой клетке в предыдущей таблице), писать не будем (табл. 17).
Таблица 17
| Потребители | |||||
| В 1 | В 2 | В 3 | В 4 | ||
| Поставщики | А 1 | 1 | 7 | 2 | 0 |
| А 2 | 3 | 11 | 5 | 0 | |
| А 3 | 4 | 10 | 8 | 0 |
12. Как и прежде, для новой распределительной таблицы найдем потенциалы  и
и  всех поставщиков и потребителей, решив систему линейных алгебраических уравнений:
всех поставщиков и потребителей, решив систему линейных алгебраических уравнений:
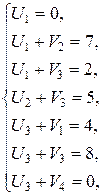
составленную, во-первых, из уравнения  , во-вторых, из уравнений
, во-вторых, из уравнений 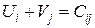 для каждой загруженной клетки: для клетки (1; 2) с тарифом 7, для клетки (1; 3) с тарифом 2, для клетки (2; 3) с тарифом 5, для клетки (3; 1) с тарифом 4, для клетки (3; 3) с тарифом 8 и для клетки (3; 4) с тарифом 0. Значения потенциалов
для каждой загруженной клетки: для клетки (1; 2) с тарифом 7, для клетки (1; 3) с тарифом 2, для клетки (2; 3) с тарифом 5, для клетки (3; 1) с тарифом 4, для клетки (3; 3) с тарифом 8 и для клетки (3; 4) с тарифом 0. Значения потенциалов  и
и  , являющиеся решением этой системы, запишем в распределительную таблицу (табл. 18).
, являющиеся решением этой системы, запишем в распределительную таблицу (табл. 18).
Таблица 18
| Потребители | Ui | |||||
| В 1 | В 2 | В 3 | В 4 | |||
| Поставщики | А 1 | 1 | 7 | 2 | 0 | |
| А 2 | 3 | 11 | 5 | 0 | ||
| А 3 | 4 | 10 | 8 | 0 20 | ||
| Vj | –2 | –6 |
13. Снова для каждой незагруженной клетки (i; j) вычислим разность 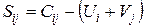 :
:
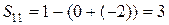 ;
;
 ;
;
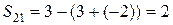 ;
;
 ;
;
 ;
;
 .
.
Клетку (3; 2), соответствующую отрицательной разности 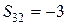 , пометим знаком «+». Затем построим замкнутый контур по указанным выше правилам, обходя этот контур, например, по часовой стрелке, поставим в его углах поочередно знаки «–» и «+» (табл. 19).
, пометим знаком «+». Затем построим замкнутый контур по указанным выше правилам, обходя этот контур, например, по часовой стрелке, поставим в его углах поочередно знаки «–» и «+» (табл. 19).
Таблица 19
| Потребители | Ui | |||||
| В 1 | В 2 | В 3 | В 4 | |||
| Поставщики | А 1 | 1 |  7
50 – 7
50 –
| 2 0 + | 0 | |
| А 2 | 3 | 11 | 5 | 0 | ||
| А 3 | 4 | 10 + | 8 20 – | 0 20 | ||
| Vj | –2 | –6 |
14. Построим следующую распределительную таблицу, в которую перенесем без изменений из предыдущей таблицы, во-первых, все тарифы перевозок, во-вторых, загрузки 80, 50, 20 клеток (2; 3), (3; 1), (3; 4), не помеченных знаками «+» и «–». Затем вычислим новые загрузки клеток со знаками «+» и «–». Для этого среди загрузок 50 и 20 клеток (1; 2) и (3; 3), помеченных знаком «–», выберем минимальную, т. е. 20. Выбранную минимальную загрузку 20 мы теперь в клетках со знаком «–» отнимем, а в клетках со знаком «+» прибавим к имеющимся там загрузкам. Отметим, что в клетке (3; 3) появится в результате вычитания нулевая загрузка, следовательно, в новой таблице в данной клетке нулевую загрузку писать не будем (табл. 20).
Таблица 20
| Потребители | |||||
| В 1 | В 2 | В 3 | В 4 | ||
| Поставщики | А 1 | 1 | 7 | 2 | 0 |
| А 2 | 3 | 11 | 5 | 0 | |
| А 3 | 4 | 10 | 8 | 0 |
15. Для новой таблицы найдем потенциалы  и
и  поставщиков и потребителей. Для этого решим систему линейных алгебраических уравнений:
поставщиков и потребителей. Для этого решим систему линейных алгебраических уравнений:
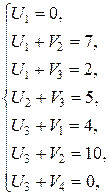
составленную, во-первых, из уравнения  , во-вторых, из уравнений
, во-вторых, из уравнений 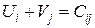 для каждой загруженной клетки (i; j): для клетки (1; 2) с тарифом 7, для клетки (1; 3) с тарифом 2, для клетки (2; 3) с тарифом 5, для клетки (3; 1) с тарифом 4, для клетки (3; 2) с тарифом 10, наконец, для клетки (3; 4) с тарифом 0. Значения потенциалов
для каждой загруженной клетки (i; j): для клетки (1; 2) с тарифом 7, для клетки (1; 3) с тарифом 2, для клетки (2; 3) с тарифом 5, для клетки (3; 1) с тарифом 4, для клетки (3; 2) с тарифом 10, наконец, для клетки (3; 4) с тарифом 0. Значения потенциалов  и
и  , являющиеся решением этой системы, укажем в распределительной таблице (табл. 21).
, являющиеся решением этой системы, укажем в распределительной таблице (табл. 21).
Таблица 21
| Потребители | Ui | |||||
| В 1 | В 2 | В 3 | В 4 | |||
| Поставщики | А 1 | 1 | 7 | 2 | 0 | |
| А 2 | 3 | 11 | 5 | 0 | ||
| А 3 | 4 | 10 | 8 | 0 20 | ||
| Vj | –3 |
16. Снова для каждой незагруженной клетки (i; j) вычислим разность 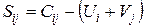 :
:
 ;
;
 ;
;
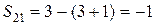 ;
;
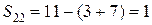 ;
;
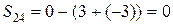 ;
;
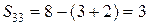 .
.
Клетку (2; 1), соответствующую отрицательной разности  , пометим знаком «+». Затем построим замкнутый контур по указанным выше правилам. Обратите особое внимание на вид этого контура (см. табл. 22). Обходя построенный контур в каком-нибудь направлении, поставим в его углах поочередно знаки «–» и «+».
, пометим знаком «+». Затем построим замкнутый контур по указанным выше правилам. Обратите особое внимание на вид этого контура (см. табл. 22). Обходя построенный контур в каком-нибудь направлении, поставим в его углах поочередно знаки «–» и «+».
Таблица 22
| Потребители | Ui | |||||
| В 1 | В 2 | В 3 | В 4 | |||
| Поставщики | А 1 | 1 |  – 7 – 7
| +2 | 0 | |
| А 2 |  + 3 + 3
| 11 | 5 80 – | 0 | ||
| А 3 | 4 50 – | 10 20 + | 8 | 0 20 | ||
| Vj | –3 |
Отметим, что клетка (2; 2) не является угловой для данного контура – в ней происходит лишь самопересечение линии контура, поэтому в клетке (2; 2) не ставим знак «+» или «–».
Построим следующую распределительную таблицу, в которую перенесем без изменений из предыдущей таблицы, во-первых, все тарифы перевозок, во-вторых, загрузку 20 клетки (3; 4), не помеченной знаком «+» или «–». Затем вычислим новые загрузки клеток со знаками «+» и «–». Для этого среди загрузок 30, 80, 50 клеток (1; 2), (2; 3), (3; 1), помеченных знаком «–», выберем минимальную, т. е. 30. Эту загрузку 30 мы теперь в клетках со знаком «–» отнимем, а в клетках со знаком «+» прибавим к имеющимся там загрузкам. При этом отметим, что в клетке (1; 2) появится в результате вычитания нулевая загрузка, следовательно, в новой таблице в данной клетке нулевую загрузку писать не будем (табл. 23).
Таблица 23
| Потребители | |||||
| В 1 | В 2 | В 3 | В 4 | ||
| Поставщики | А 1 | 1 | 7 | 2 | 0 |
| А 2 | 3 | 11 | 5 | 0 | |
| А 3 | 4 | 10 50 | 8 | 0 |
17. Для новой распределительной таблицы найдем потенциалы  и
и  поставщиков и потребителей. С этой целью решим систему линейных алгебраических уравнений:
поставщиков и потребителей. С этой целью решим систему линейных алгебраических уравнений:

составленную из уравнения  , а также уравнений
, а также уравнений 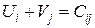 для каждой загруженной клетки (i; j): для клетки (1; 3) с тарифом 2, для клетки
для каждой загруженной клетки (i; j): для клетки (1; 3) с тарифом 2, для клетки
(2; 1) с тарифом 3, для клетки (2; 3) с тарифом 5, для клетки (3; 1) с тарифом 4, для клетки (3; 2) с тарифом 10 и для клетки (3; 4) с тарифом 0. Значения потенциалов  и
и  , являющиеся решением этой системы, укажем в распределительной таблице (табл. 24).
, являющиеся решением этой системы, укажем в распределительной таблице (табл. 24).
Таблица 24
| Потребители | Ui | |||||
| В 1 | В 2 | В 3 | В 4 | |||
| Поставщики | А 1 | 1 | 7 | 2 | 0 | |
| А 2 | 3 | 11 | 5 | 0 | ||
| А 3 | 4 | 10 | 8 | 0 20 | ||
| Vj | – 4 |
18. Для каждой незагруженной клетки (i; j) вычислим разность 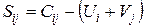 :
:
 ;
;
 ;
;
 ;
;
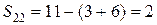 ;
;
 ;
;
 .
.
Как видим, все эти разности неотрицательны, следовательно, найден оптимальный план перевозок. Согласно ему, от поставщика А 1 потребителю В 3 нужно перевезти 50 единиц груза, от поставщика А 2 потребителям В 1 и В 3 – соответственно 30 и 50 единиц груза, а от поставщика А 3 потребителям В 1 и В 2 – 20 и 50 единиц груза соответственно. Учитывая, что В 4 – фиктивный поставщик (об этом нам напоминают нулевые тарифы в графе В 4), получаем, что 20 единиц груза (загрузка клетки (3; 4)) останутся невывезенными у поставщика А 3. Транспортные расходы при таком плане перевозок составят:
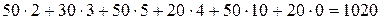
(сумма произведений загрузок клеток и соответствующих тарифов перевозок).
Date: 2016-07-25; view: 385; Нарушение авторских прав