Вероятность суммы событий.

Сформулируем и докажем правило вычисления вероятности суммы двух событий A и B.

Для этого разобьем каждое из множества элементарных событий, составляющих события A и B на две части: 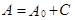; 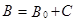, где

объединяет все элементарные события , входящие только в A и B, а C состоит из всех тех элементарных событий, которые одновременно входят и в A, и в B, ò. å. С = A × B.

Пользуясь определением вероятности и свойством 4, имеем:

P (A) ,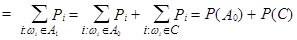

.

В то же время (свойство 4)

.

Последнее равенство известно, как теорема сложения вероятностей двух совместных событий. Для несовместных P (C)=0, поэтому P (A + B) = P (A) + P (B)

Пример 1. В некоторой игре можно выиграть или вещь, или деньги. Тогда пространство элементарных событий где ={вещь}, ={деньги}, ={проигрыш}. Пусть А ={выиграть вещь}, B ={выиграть деньги}, P (A) = 0,4; P (B) = 0,2; C ={выигрыш}=

P (A + B) = P (A) + P (B) = 0,6.

Пример 2. Банк «А» может обанкротиться с вероятностью 0,05, а банк «B» – с вероятностью 0,03 независимо от банка «А». Вычислить вероятность того, что хотя бы один банк обанкротится, если известно, что

P (C) = P (A) + P (B) – P (A×B) = 0,05 + 0,03 – 0,0015 = 0,08 – 0,0015 = 0,0785.

Обобщение последней суммы на случай более чем двух слагаемых приводит к громоздким вычислениям, поэтому используется окольный путь для вычисления вероятности суммы совместных событий. Воспользуемся тем, что сумма «хотя бы одно событие» и противоположное ему «ни одного» является событием достоверным, а вероятность достоверного события равна единице. Тогда вероятность суммы произвольных событий равна разности между единицей и вероятностью произведения противоположных им событий. Пусть являются совместными событиями. Используем свойство событий

и запишем

.

.

Пример. Акционер имеет 4 акции. Пусть событие (i= 1, 2, 3, 4) состоит в том, что i -ая акция обесценилась. Известно, что вероятности обесценивания акций равны соответственно 0,05, 0,10, 0,30, 0,04, а вероятность того, что одновременно не обесценятся все четыре акции равна 0,58. Найти вероятность того, что хотя бы одна акция обесценилась.

Решение: , ни одна акция не обесценится

,

.

Приведем сводную таблицу, которая содержит формулы для расчета (и численный пример) вероятности при независимых событиях A и B.

Событие	Вероятность	Пример P (A)=0,10; P (B)=0,01
Оба		P =0,001
Ни одного		P =0,999
Или А, или В, но не оба вместе		P =0,108
Или А, или В, или оба вместе		P =0,109
Ни А, ни В		P =0,891
Или оба, или ни одного		P =0,892
A, но не B		P =0,099

Date: 2016-07-25; view: 387; Нарушение авторских прав