Функции тангенс и котангенс.

Вопрос 1.

Функции синус и косинус.

Окружность радиуса r=1 с центром в начале координат называют единичной окружностью. Пусть точка P_α единичной окружности получена путем поворота точки P₀ на угол α радиан против часовой стрелки. Ордината точки P_α - это синус угла α, а абсцисса этой точки - косинус угла _α.

Далее и везде будем считать, что значения всех углов задано в радианах, если только специально не указаны другие единицы измерения. Таким образом, если написано α=1, то подразумевается, что угол α равен 1 рад.

Определение. Числовые функции, заданные формулами y=sin(x) и y=cos(x) называют соответсвенно синусом и косинусом (обозначают соответсвенно sin и cos).

Область определения этих функций - вся прямая действительных чисел. Область значения этих функций - отрезок [-1;1]:

D(sin)=D(cos)=R

E(sin)=E(cos)=[-1;1]

Функция sin(x) является нечетной функцией:

sin(-x)=-sin(x)

Функция cos(x) является четной функцией:

cos(-x)=cos(x)

Обе функции sin(x) и cos(x) являются периодическими с периодом T=2π:

sin(x+Tn)=sin(x)

cos(x+Tn)=cos(x), где n - любое целове число.

Функции тангенс и котангенс.

Числовые функции, заданные формулами y=tg(x) и y=ctg(x), называют соответственно тангенсом и котангенсом (и обозначают соответственно tg и ctg).

Областью определения функции тангенс является множество всех чисел x кроме тех, где cos(x)=0: x≠π/2+πn, где n - любое целое число.

Областью определения функции котангенс является множество всех чисел x кроме тех, где sin(x)=0: x≠πn, где n - любое целое число.

Проведем касательную l к единичной окружности в точке P₀. Пусть α - произволньое число, для тогорого cos(α)≠0. Тогда точка P_α(cos(α),sin(α)) не лежит на оси ординат, и, следовательно, прямая OP_α пересекает l в некоторой точке T_α с абсциссой 1. Необходимо найти ординату этой точки.

Заметим, что прямая OP_α проходит через точки О(0,0) и P_α(cos(α),sin(α)), поэтому она имеет уравнение y=xtg(α). Абсцисса T_α=1, из вышеприведенного уравнения прямой находит ординату T_α - tg(α).

Итак, ордината точки пересечения прямых OP_α и l равна tg(α). Прямую l иногда называют линией тангенсов.

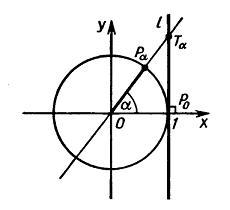
Нетрудно по аналогии показать, что абсцисса точки C_α пересечения прямой OP_α с касательной m к единичной окружности, проведенной через точку P_π/2, равно ctg(α) при sin(&alpha)≠0. Прямую m называют линией котангенсов.

Область значений тангенса (котангенса) - вся числовая прямая. Докажем это для функции tg.

Пусть y₀ - произвольное действительное число. Рассмотрим точку T(1,y₀). Следуя показанному выше, тангенс угла TOX равен y₀. Следовательно, функция tg принимает любое лействителньое значение.

Функции тангенс и котангенс обладают следующими свойствами:

1. tg(-x)=-tg(x), ctg(-x)=-ctg(x) - функции тангенс и котангенс являются нечетными функциями.

2. tg(x+πn)=tg(x), ctg(x+πn)=ctg(x), n - целое.

Вопрос 2.

Date: 2016-07-25; view: 590; Нарушение авторских прав