
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Информация и информатика.
|
|
Г.
§ Понятие информации.
Вся жизнь человека, так или иначе связана с накоплением и обработкой информации, которую он получает из окружающей среды, используя органы чувств.
Как научная категория, информация составляет предмет изучения для самых различных дисциплин. Это физика, информатика, математика, философия, кибернетика и др…
Несмотря на это, строгого определения, что такое информация пока не существует, а вместо него обычно используют понятие об информации. Понятие отличается от определения тем, что разные дисциплины в разных областях науки и техники вкладывают в него различный смысл с тем, чтоб оно в наибольшей степени соответствовало предметам и задачам в конкретной дисциплине.
Имеется много определений понятия информации.
С философской точки зрения – это отражение реального мира.
В частном или прикладном случае – это сведения, являющиеся объектом переработки.
Изначально смысл слова информация трактовался как нечто, присущее человеческому сознанию (знания, сведения, известия, передаваемые людьми устным, письменным или др. способом).
Затем смысл слова «информация» стал расширяться.
Под информацией стали понимать способность отображать одним реальным объектом другие, а сам факт отражения и означает присутствие в нём информации об отражаемом объекте. Иначе говоря, как только состояние одного объекта окажется в соответствии с состоянием другого объекта – это значит, что один объект отражает другой, т.е. содержит информацию о нём.
Напр: показание частотомера или напряжение на клеммах тахогенератора (динамо-машина) и скорость вращения вала электродвигателя.
Особенностью информации является то, что она проявляется при взаимодействии объектов. Причем обмен информации может совершаться не вообще между любыми объектами, а только между теми из них, которые образуют организованную систему (структуру), элементами которой могут быть как люди, так и например, человек и устройство или два устройства. Таким образом, понятие «информация» обычно предполагает наличие двух объектов: источника и приемника информации. От источника к приемнику информация передается в виде сигналов различной физической природы, которые распространяются в определенной среде.
Сигнал – это физический процесс, несущий сообщение или информацию о событии или состоянии объекта наблюдения.
Различают аналоговую и дискретную информацию.
Из вышесказанного следует:
- информация объективна, т.к. это свойство материи – отображение;
- информация проявляется в виде сигналов и лишь при взаимодействии объектов;
- одна и та же информация различными получателями может быть интерпретирована (понята) по разному, в зависимости от степени подготовленности «получателя».
Г.
§ Основные функции информации.
- познавательная (получение новой информации); Она реализуется через синтез, представление, хранение, восприятие.
- коммуникативная или функция общения; Она реализуется через передачу и распределение.
 - управленческая (сформировать необходимое или желаемое поведение управляемого объекта или системы, в которой получают информацию).
- управленческая (сформировать необходимое или желаемое поведение управляемого объекта или системы, в которой получают информацию).
§ Информационные процессы и системы.
В автоматических (технических) или автоматизированных (человек - машина) системах информация используется для выражения управляющих воздействий.
В таких системах можно выделить этапы прохождения информации, каждый из которых характеризуется определенными действиями. Последовательность действий, выполняемых с информацией, называется информационным процессом, а системы, которые их реализуют – называются информационными системами.
§ Основные этапы прохождения информации в системах.
1. Сбор;
2. Преобразование;
3. Передача;
4. Обработка;
5. Хранение;
6. Воспроизведение (отображение).
Первый этап: осуществляется целенаправленное извлечение и анализ информации об объекте или процессе. Основная цель → выделить полезную информацию от паразитной (щитов).
Второй этап: информация преобразуется (аналоговая → в цифровую; кодирование информации). В результате получается сигнал в удобной для пользователя форме.
Сигналы могут быть разной физической природы, но наиболее используемые: электрические, электромагнитные, оптические.
С появлением ЭВМ, как универсального преобразователя информации – появилось понятие данные и обработка данных.
Данными называют – набор фактов и сведений, занесённых на те или иные носители.
На этапе хранения информация записывается запоминающими устройствами, чаще всего полупроводниковые или магнитные носители.
Цель этапа отображения – представить информацию в желаемом для человека виде.
Управление и информация служат основными понятиями кибернетики.
Кибернетика (с греч. – искусство управления) – наука об общих законах получения, хранения, передачи, переработки информации.
Примеры кибернетических систем: какие-либо регуляторы, ЭВМ, человеческий мозг. Каждая такая система представляет собой множество взаимосвязанных объектов, способных воспринимать, запоминать, перерабатывать информацию или обмениваться ею.
Современная кибернетика состоит из ряда разделов, представляющих собой самостоятельные научные направления. Её основой являются: теория информации, теория алгоритмов, теория автоматов, теория управления.
Кибернетика разрабатывает общие принципы создания управления, а основным техническим средством является ЭВМ, поэтому развитие кибернетики жестко связано с развитием ЭВМ.
Понятие кибернетики, как научный термин, введено в первой половине 19-го века французским физиком – Ампером, который назвал кибернетику наукой, занимающейся изучением искусства управления обществом. А основоположником кибернетики, как технической науки, стал – Норберт Виннер, в 1948 году, после опубликования книги «Кибернетика или управление и связь в животном мире и машине».
§ Основные законы кибернетики.
1. Всякое управление – есть целенаправленные процесс;
2. Всякое управление – есть информационный процесс, который состоит из:
- сбора информации;
- обработки информации;
- хранения и передачи информации;
3. Всякое управление обычно осуществляется в замкнутом контуре.
§ ИНФОРМАТИКА.
Очень долго основным средством для обработки и передачи информации был человеческий мозг, язык и слух человека. Существенный скачок произошел с появление письменности. С появлением электричества появились: телефон, телеграф, радио. => Это позволило передавать и накапливать информацию в другом виде и большем объеме.
В 20-м веке произошло серьёзное развитие науки и промышленности. => Вырос объем поступаемой информации и человек оказался не в состоянии воспринимать и обрабатывать все для него предназначенное. Возникла необходимость классифицировать информацию, организовать её хранение, обеспечивать доступ и т.д.
Исследования, позволяющие разрешить эти проблемы стали называть – информатикой.
В этом смысле информатика – это научная дисциплина, изучающая структуру и общие свойства научной информации. Очень долго информатика являлась базой библиотечного дела. С появлением ЭВМ, появилась новая промышленная отрасль, средства и методы электронной обработки информации. ЭВМ стали обрабатывать числовую, текстовую, графическую … информацию.
В результате информация стала товаром. Её нужно принять, записать, преобразовать к удобному, для анализа, виду, затем обработать, а результаты представить в удобном, для исследования, виде.
Это и есть задачи, которые являются общими для всех наук при обработке информации с помощью ЭВМ, а научным фундаментом для их решения стала «новая» наука – информатика.
Г.
Французский термин – informatique → information и automatique, что означает – информационная автоматика или автоматизированная переработка информации. Отсюда информатика – это отрасль науки, которая изучает структуру и общие свойства научной информации, а так же вопросы, связанные с её сбором, хранением, поиском, переработкой, распространением и использованием в различных сферах нашей деятельности.
Как комплексная научная дисциплина, информатика связана с:
- философией и психологией, через учение об информации и теорию познания;
- математикой, через теорию математического моделирования, дискретную математику, математическую логику и теорию алгоритмов;
- лингвистикой, через учение о формальных языках и знаковых системах;
- кибернетикой, через теорию управления и теорию информации;
- физикой и химией, электроникой и радиотехникой, через «начинку» ЭВМ.
§ Количество и качество информации.
§ Уровни передачи информации.
При реализации информационных процессов для передачи информации используются различные знаки или символы естественного или искусственного языка, позволяющие выразить её в некоторой форме, называемой сообщением.
Сообщение – это форма представления информации в виде совокупности знаков, используемых для её передачи.
С точки зрения семиотики (науки, занимающейся исследованием свойств знаков и знаковых систем), сообщение может изучаться на 3-х уровнях:
- синтаксическом, где рассматривается внутренние свойства сообщений, т.е. отношение между знаками, отражающими структуру данной знаковой системы;
/* внешние свойства сообщений изучают на семантическом и прагматическом уровнях */
- семантическом, анализируются отношения между знаками и обозначаются ими или предметами, т.е. рассматривают смысловое содержание сообщения и его отношение к источнику информации;
- прагматическом, где рассматривается отношение между сообщением и его получателем, т.е. потребительское содержание сообщения.
§ Проблемы уровней передачи информации.
Проблемы синтаксического уровня касаются создания теоретических основ построения информационных систем с целью повышения их надежности и эффективности использования. Это чисто технические проблемы. Совершенствование методов передачи сообщений и их материальных носителей (сигналов).
Здесь рассматриваются проблемы доставки получателю сообщений, как совокупности знаков, учитывая при этом тип носителя и способ представления информации, скорость передачи и обработки, надежность и точность кодированной информации и абсолютно не волнует смысловое содержание сообщения и его целевое предназначение.
На этом уровне информацию обычно называют – данными, т.к. смысловая сторона сообщения не имеет никакого значения. Современная теория информации в основном исследует проблемы этого уровня.
Здесь есть понятие – количество информации, т.к. смысловое содержание информации не рассматривается, поэтому иногда говорят, что теория информации находится на синтаксическом уровне.
Теория информации – это раздел кибернетики, в котором математическими методами изучают способы измерения количества информации, содержащейся в каких-либо сообщениях, а так же изучают способы передачи информации.
Проблемы семантического уровня связаны с учетом смысла передаваемой информации. Здесь рассматривается смысловые связи, формируются понятия, выявляется смысл и содержание информации. Эти проблемы очень сложны, т.к. содержательная часть информации больше зависит от получателя, чем от семантического (отправителя) сообщения, представленного на каком-либо языке.
На прагматическом уровне интересуют последствия от получателя и использование информации потребителем. Проблема связана с определением ценности и полезности информации при выработке потребителем решения для достижения своей цели. Сложность заключается в том, что для различных получателей одна и та же информация может иметь разную ценность.
§ Мера информации.
Для каждого из рассмотренных выше уровней передачи информации существуют свои подходы к изменению количества и свои меры информации.
§ Меры информации синтаксического уровня.
Так как здесь оперируют с обезличенной информацией (не выражающей смыслового отношения к объекту), данная мера дает возможность оценки информационных потоков в различии, по своей природе, объектов – это системы связи и управления, вычислительные машины, живой организм и т. д.
Здесь вводят 2 параметра данных:
- объем информации (объемный подход - Vд);
- количество информации (вероятный или энтропийный подход - I).
§ Объемный подход.
Если принять символ за единицу, то объем сообщения равен количеству символов. Существуют разные алфавиты (СС).
V – количество символов.
Алфавиты систем исчисления:
в 10-ой: 1 разряд – 1 дит (4 бита);
в 2-ой: 1 разряд – 1 бит.
§ Энтропийный (вероятностный) подход.
Он основывается на том, что факт получения информации связан с уменьшением неопределенности (энтропии) системы. Отсюда количество информации в сообщении определяется как мера неопределенности состояния данной системы после получения сообщения.
Здесь под понятием «неопределенность» понимается - на сколько мало известно наблюдателю о данной системе. Получаемая информация снижает неопределенность (энтропию) системы. Таким образом при энтропийном подходе под информацией понимается количественная величина исчезнувшей, в ходе опыта, неопределенности.
В качестве меры неопределенности вводится энтропия H, а количество информации I=Hapr-Haps, где Hapr – априорная энтропия о состоянии системы, Haps – апостериорная система.
Априори – понятие, которое характеризует значение, предшествующее опыту и не зависимое от него.
Апостериори – понятие, которое характеризует значение, происходящее их опыта.
Допустим, в ходе испытания, имевшаяся неопределенность снята, получен корректный результат, тогда Haps=0 => I=Hapr.
Напр.: в качестве исследуемой системы рассмотрим дискретный источник информации, т. е. физическую систему, имеющую конечное состояние ({ai}=1, 2,…, n).
В теории информации все множество состояний системы называют абстрактным алфавитом или алфавитом источника сообщений (A={а1, а2,…, аn}).
Относительное состояние (ai) – буква или символ алфавита. Такая система, в каждый момент времени, может принять одно из этого множества состояний. Различие состояний реализуется в следствии выбора их источником, а выбор осуществляется хаотично. В общем случае источник характеризуется n – состояниями, каждое из которых имеет вероятность появления pi.

Меру неопределенности выбора состояния источников можно рассматривать и как меру количества информации, получаемой при полном устранении неопределенности относительно состояний источника. Эта мера должна удовлетворять ряду естественных условий, одним из которых является необходимость монотонного возрастания количества получаемой информации с увеличением возможности выбора, т. е. с увеличением числа N-возможных состояний источника, при этом, не дополненные состояния, вероятность появления которых равна 0, не должны учитываться, т. к. они не меняют неопределенность.
Из сказанного следует, что, казалось бы, за меру неопределенности можно было бы взять число состояний – N, предположив, что состояния равновероятностные, но это не так.
При N=1 (неопределенность отсутствует) – такая мера давала бы значение, равное 1, а должен быть 0. Поэтому, в качестве меры неопределенности источника с равновероятностным соотношением приняли log числа состояний. H=ln(N) (H(A)=ln(N))
В данном случае основание логарифма не имеет принципиального значения, а определяет масштаб или единицу измерения (биты – основание 2; наты – основание 1; диты – основание 10)
Эту формулу предложил американский ученый – Хартли, в начале 20-го века, т. к. в современной информационный технике используется двоичная система, то для изменения неопределенности обычно используют основание – 2 (H=log2(N)).
Напр.: для снятия неопределенности в ситуации из 2-х равновероятностных событий – нужен один опыт => 1 вид информации.
4 события – 2 бита;
8 событий – 3 бита.
Т. е. количество информации равно степени, в которую нужно возвести число 2, чтобы получить число, равновероятностных вариантов выбора. Эта мера позволяет решать определенные практические задачи, когда все возможные состояния источника – равновероятны, что практически никогда не бывает.
Американский ученый Шеннон обобщил понятие меры неопределенности (H) на случай разновероятностных событий. Эту меру, представляющую собой неопределенность, приходящуюся в среднем на одно состояние, называют энтропией дискретного источника информации.


т. к. двоичная система счисления (СС)
В случае равновероятностных событий (выборов), данная формула преобразуется в формулу Хартли.

Используя формулы Хартли и Шеннона, можно определить избыточность (D) алфавита источника сообщений (А), которое покажет на сколько рационально применяются символы данного алфавита.
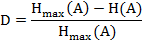

max возможная энтропия, определяемая по формуле Хартли, а H(A) – по формуле Шеннона
Суть данной меры заключается в том, что при равновероятностном выборе, ту же информационную нагрузку на знак можно обеспечить, используя алфавит меньшего объема, чем в случае с неравно вероятностным выбором.
Напр.: сравним русский и латинский алфавиты на основе определения вероятности использования букв.



Г.
§ Меры информации семантического уровня.
Для измерения смыслового содержания информации, т. е. её количества на семантическом уровне, наибольшее распространение получила тезаурусная мера, которая связывает семантические свойства информации со способностью пользователя принимать поступившее сообщение.
Действительно для получения и использования полученной информации, пользователь должен обладать определенным запасом знаний.
Полное незнание предмета не позволяет извлечь полезную информацию, для этого, по мере роста знаний о предмете, растет и количество информации.
Назовем имеющиеся у пользователя знания о предмете – тезаурусом (набор слов, понятий, названий объектов, связанных смысловыми связями), отсюда количество информации, содержащейся в некотором сообщении можно оценить степенью изменения индивидуального тезауруса, под воздействием данного сообщения.
Тезаурус – это совокупность сведений, которыми располагает пользователь или система.
В зависимости от соотношений между смысловым содержанием информации (S) и тезаурусом пользователя (Sp) изменяется и количество семантической информации IS, воспринимаемой пользователем. Графически это выглядит следующим образом:
Рассмотрим 2 случая:
Sp= 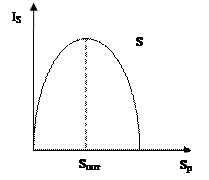 0 – пользователь не воспринимает информацию;
0 – пользователь не воспринимает информацию;
Sp=∞ - пользователь знает «все», то он тоже не получает нужной ему информации.
max количество информации потребитель приобретает при согласовании смыслового содержания информации с тезаурусом пользователя.
Таким образом количество семантической информации в сообщении является величиной относительной. Относительной мерой количества семантической информации может служить коэффициент содержательности (C), который равен отношению количества семантической информации к её объему. C=IC/Vi
§ Меры информации прагматического уровня.
Оно определяет полезность информации, для достижения пользователем поставленной цели. Это тоже относительная величина (Харкевич А. А.). Он предложил принять за меру ценности информации такое её количество, которое необходимо для достижения поставленной цели, т. е. рассчитать приращение информации для достижения поставленной цели.
I=log2p1-log2p2=log2p1/p2, где p2 – вероятность достижения цели до получения вероятности, а p1 – после получения информации.
 Ценность информации измеряется в битах.
Ценность информации измеряется в битах.
p2=1/2 p2=1/2 p2=1/2
p1=3/6 p1=1/6 p1=4/6
I=0 I=-1,58 I=0,42
Здесь приняты одинаковые значения числа исходов: 2 и 6. Исходное получение точки О. На основании полученной информации, происходит переход в точку 1. Цель обозначена – Х. Благоприятные исходы отображены линиями, идущими к цели. Ценность информации во всех 3-х случаях.
В примере б – получена отрицательная ценность информации, такую информацию, которая увеличивает исходную неопределенность и уменьшает вероятность достижения цели, называют дезинформацией, т. е. в примере б мы получили дезинформацию 1,58 двоичные единицы.
§ Качество информации.
Эффект применения и качество работы любых систем во многом определяется качеством информации, на основе которой вырабатывается управляющее воздействие.
Выделяют внутренние и внешние качества информации:
- внутренние – содержательность;
- внешние – защищенность.
Содержательность – это свойство, присущее, собственно, информации и сохраняющееся при переносе в другую систему.
Защищенность – это свойство, присущее информации, находящейся или используемой в определенной системе.
Содержательность – это совокупность сведений о конкретном объекте или системе. Она содержится в сообщениях, воспринимаемых получателем, и отражает семантическую емкость информации. Как правило, она используется для выработки управляющего воздействия. Содержательность определяется значимостью и кумулятивностью. Состояниями значимости является полнота и идентичность.
Полнота характеризуется мерой достаточности информации для решения определенных задач и принятия правильного решения. Эта мера – относительная, т. к. оценивается относительно, вполне определенной задачей.
Как неполная, так и избыточная информация – снижают эффективность принимаемых пользователем решений.
Идентичность – свойство, заключающееся в соответствии содержательной информации к состоянию объекта.
Кумулятивность – способность небольшим объемом информации отражать действительность.
У кумулятивности информации можно выделить два свойства:
- гомоморфизм;
- избирательность.
Гомоморфизм – свойство содержательной информации, связанное с достаточно полным отражением действительности, наименьшим количеством символов.
Избирательность – то же, что и гомоморфизм, но с учетом квалификации, опыта и других качеств потребителей информации.
Защищенность, присущая информации, находящейся или используемой только в определенной системе. Основное свойство – не допускать случайного или целенаправленного искажения. Это обеспечивается системой контроля и защиты информации в конкретной информационной системе. Это свойство можно подразделить на достоверность, конфиденциальность и сохранность.
Достоверность – степень соответствия, в пределах желаемой точности, информации её истинному значению.
Конфиденциальность – характеризуется достаточностью, так и скрытностью.
Достоверность характеризуется в возможности использования информации получателем или пользователем, с скрытность - степенью маскировки информации, и отражает способность противостоять раскрытию смысла информации (семантическая скрытность).
Требуемый уровень конфиденциальности достигается путем дополнительных преобразований информации.
Сохранность – характеризуется степенью готовности данных, в котором все данные стремятся к целевому использованию, и определяются системой контроля и защиты обеспечить постоянное наличие и своевременное предоставление информации, необходимой для решения каких-либо задач.
§ Виды и формы представления информации в информационных системах.
Всю окружающую нас информацию можно классифицировать по различным признакам.
Напр.: по признаку – область возникновения.
Информацию, отражающую процессы и явления неодушевленной природы, - называют элементарной или механической; процессы животного мира – биологической; человеческого рода – социальной.
Информация, используемая человеком (личная, специальная), может быть объективна и субъективна.
В автоматических информационных системах выделяют структурную (преобразующую) информацию объектов и систем, заключенных в структурах системы, её элементах управления, алгоритмах и программах переработки.
В содержательную (специальную, осведомляющую) систему они извлекаются, например, из сообщений или команд.
Структурная связана с качеством информационных процессов в системе, содержательная – с внешним целевым эффектом.
В настоящее время во всех вычислительных системах информация представляется в виде элементарных сигналов: аналоговых или дискретных.
Аналоговая – в вид одного сигнала, дискретная – в виде нескольких сигналов.
В аналоговой форме величины могут принимать любые значения в определенном диапазоне, и количество этих значений – бесконечновелико. Отсюда и название – аналоговая, непрерывная (нет разрывов между значениями). В дискретной форме – величины принимают не все возможные, а лишь определенные значения, количество значений дискретной величины всегдаконечно. Отсюда очевидно, что при создании (использовании) непрерывной формы представления информации, для создания электрической машины, потребуется меньшее количество устройств, т. к. каждая величина представляется одним, а не несколькими сигналами, но эти устройства будут сложнее, т. к. они должны уметь различать значительно большее число состояний сигналов.
Такая форма представления используется в аналоговых вычислительных машинах, которые в основном предназначены для решения задач моделирования, процессов и систем анализа и синтеза их работы, но из-за сложности тех-реализации таких устройств (напр.: для выполнения логических операций с непрерывным сигналом, длительного решения и точного суммирования последних), АВМ не могут эффективно решить задачи, связанные с хранением и обработкой больших объемов информации, что легко реализуется при использовании цифровой или дискретной формы представления, которая применяется в ЭВМ.
Г.
§ Представление информации в цифровых автоматах системы счисления.
Системы счисления (СС) – это совокупность приемов и правил, наименования и обозначения чисел, позволяющих установить взаимно-однозначное соответствие между любым числом и его представлением в виде конечного числа символов.
В любой СС выбирается алфавит, представляющий собой совокупность символов, слов или знаков. С его помощью, в результате неких операций можно представить любое количество.
Изображение любого количества – называется числом, а символы алфавита – цифрами. Символы должны быть разными и значение каждого должно быть известно.
Наиболее распространенные – десятичные СС (из пальцевого счета). Завезли её в Европу из Индии (арабы) => 0…9 – арабские цифры.
Существуют другие СС:
1 фут – 12 дюймов;
1 шиллинг – 12 пенсов.
Все СС подразделяются на: позиционные и непозиционные.
§ Непозиционные СС.
В них символы, обозначающие то или иное количество, не меняют своего значения в зависимости от места положения в изображении числа. Запись такого числа:

В такой СС (непозиционной) - относится римская. (I V X L(50) C(100) D(500) M(1000))
Правила записи в римской СС:
- если цифра справа <= цифре слева, то они складываются;
- если цифра слева < цифры справа, то левая вычитается из правой.
Это довольно сложный способ записи, поэтому сейчас используют позиционные системы.
§ Позиционные СС.
Здесь значение цифры определяется её местоположением в изображении числа => отсюда название позиционная.
Упорядоченный набор символов или цифр СС – называют её алфавитом (а0, а1, а2,…, аn).
Назовем p – основанием системы. Очевидно, что p=n+1, и такая СС называется p-ичной. Основание позиционное СС – это количество различных цифр, используемых для изображения чисел в данной СС. Наиболее привычная для нас – десятичная, в которой любое число можно представить в виде полинома {многочлена}.
Напр.: A=362,149=3*102+6*101+2*100+1*10-1…

Точка, отделяющая целую часть от дробной, служит для фиксации конкретных значений в каждой позиции, в этой последовательности чисел. {A=an,an-1…a0,a-1,a-2…} И, фактически, является началом отсчета.
В общем случае для задания p-ой СС необходимо определить основание – p и алфавит, состоящий из p – различных символов. За основание можно принять число от 0-ля до 9-и. при нехватке цифр, используют буквы латинского алфавита.
Наиболее распространенные СС: двоичная, восьмеричная, десятичная и шестнадцатеричная => возможно создание множества позиционных систем.

Арифметические действия:
Очевидно, чем меньше основание СС, тем больше разрядов необходимо для отображения числа.
Арифметические действия над числами в любой позиционной системе преобразуются по одним и тем же правилам. В любой позиционно СС с любым основанием p произведение над числом pm (m-целое) сводится просто к перенесению запятой умноженного на m – разрядов вправо или влево, в зависимости от знака m.
Dec: 1112…21(710)= 1110 2(1410)
СС используют для построения на их основе различных кодов в системах передачи, хранения и использования информации.
Код – это система условных знаков или символов для представления различной информации. Любому дискретному сообщению можно приписать какой-либо порядковый номер. Измерение аналоговой величины (сравнение её с обратными мерами) так же приводит к числовому представлению информации. Передача или хранение сообщений при этом сводится к передаче или хранению чисел, которые можно выразить в какой-либо СС. Таким образом, будет получен один из кодов, основанный на данной СС.
Каждому разряду можно поставить в соответствие какой-либо электрический параметр, например амплитуду сигнала.
Представим число 365 в виде импульсов длительностью Ʈ в различных СС
. 

|
Анализ СС и построение на их основе кодов показывает, чем больше основание, тем меньше число используемых разрядов, но в этом случае изменяются требования к аппаратуре, формирующей и передающей сигнал. С точки зрения нахождения компромисса между этими показателями, оптимальной будет СС с основанием 3 и не значительно ей уступают системы с основанием 2 и 4-ре. С точки зрения простоты физической реализации, предпочтение отдается СС с основанием 2.
Г.
С ростом основания СС и логические элементы вычислительных устройств должны иметь большее число устойчивых состояний. С учетом этого в качестве эффективной системы может быть выбрано число, равное произведению количества различных символов - q, в данной СС, на величину разрядной сетки – N(q – количество символов, N – длинна разрядной сетки). C=q*N
Тогда наиболее эффективной будет система, обеспечивающая минимум данного выражения. Если принять, что каждый разряд числа представляется не одним элементом с q-устойчивыми состояниями, а q-элементами, каждый из которых имеет одно устойчивое состояние, то данный показатель «C» определит условное количество оборудования, которое нужно иметь для представления чисел в данной СС. Поэтому этот показатель (С) называют показателем системы.
Максимальное число, которое можно получить в СС с основанием q и разрядной сеткой, величиной N:
 => можно найти длину разрядной сетки – N:
=> можно найти длину разрядной сетки – N:
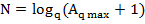
Тогда:

 |
N
Допустим, величина q – непрерывна, при этом С – функция от величины q. Если за одну единицу измерения оборудования один элемент с одним устойчивым состоянием, то для сравнения двух СС можно ввести относительный показатель экономичности – F, позволяющий сравнить любую СС с двоичной.

Проанализировав данное выражение на экстремум:  – получим минимум функции F, что соответствует значению q=2,72. При условии непрерывности q, графически это выглядит так:
– получим минимум функции F, что соответствует значению q=2,72. При условии непрерывности q, графически это выглядит так:

=> с точки зрения затрат на условное оборудование, наиболее экономичней является СС с основанием 3.
§ Перевод из одной СС в другую.
Пусть известна запись числа в СС p.
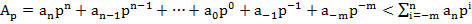 , где a с индексом i–цифры p-ичной СС.
, где a с индексом i–цифры p-ичной СС.
0≤ai<p, требуется найти запись этого числа в СС с основанием d.
 , здесь bi – цифры искомой СС. 0≤bi≤d-1
, здесь bi – цифры искомой СС. 0≤bi≤d-1
Ограничимся случаем положительных чисел, так как перевод любого числа сводится к переводу его модуля и приписыванию числу нужного знака. При переводе чисел из p-ой системы в d-ую, нужно учитывать, средствами какой арифметики будет осуществляться перевод, те в какой СС (p-ой или d-ой) должны быть выполнены все, необходимые для перевода, операции.
Пусть этот перевод осуществляется средствами d-ичной арифметики, тогда перевод Ap в Ad выполняется по правилу замещения, которое представляет вычисление полинома для p-ичной системы в новой СС, те для получения d-ого изображения p-ичного полинома необходимо все цифры a-итые и число p заменить d-ичными изображениями и выполнить арифметические операции в d-ичной CC.
Чаще всего правила замещения используются для преобразования чисел из любой СС в десятичную. Для этого случая правила нужно конкретизировать.
Перевод в десятичную систему числа A, записанного в p-ичной системе, Ap={an,an-1,an-2,…}
сводится к вычислению значения многочлена, средствами десятичной арифметики.
2 1 0 -1
Напр.: (275,6)8=2*82+7*81+5*80+6*8-1=(190,625)10
При переводе следует придерживаться правила сохранения точности изображения числа в разных системах, причем под точностью понимается значение единицы самого младшего правого разряда, используемого в записи числа или иной СС.
Пусть теперь перевод Ap в Ad должен осуществляться средствами p-ичной арифметики. В этом случае для перевода любого числа из одной СС в другую используются правила деления, для перевода целой части, и правила произведения для перевода дробной части.
§ Правила перевода целых чисел.
Для выражения чисел Ap и Ad будет выглядеть:


Здесь ai-цифры p-ичной СС, а bi- искомые цифры d-ичной СС.
Так как это одно и то же число, то можно записать: 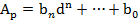 , здесь bi – искомые числа в d-ичной СС. Для определения b0 разделим обе части равенства на число d, при этом, в левой части равенства пользуемся правилами p-ичной арифметики, тк запись Ap нам известна.
, здесь bi – искомые числа в d-ичной СС. Для определения b0 разделим обе части равенства на число d, при этом, в левой части равенства пользуемся правилами p-ичной арифметики, тк запись Ap нам известна.
Выделим в частном от деления Ap/d целую и дробную части.

, но дробная часть представляет собой остаток от деления, деленный на d. Перепишем правую часть равенства в вид:

Тк pi<d, то можно записать:  => младший коэффициент b0 в разложении для Ad= (остаток + b0)
=> младший коэффициент b0 в разложении для Ad= (остаток + b0)
Для оставшейся целой части (правая часть выражения) применяем тот же самый алгоритм для определения b1 и тд.
Этот процесс продолжается до тех пор, пока неполное частное (целая часть от деления) не станет равной 0.
Тк все операции выполняются в СС с основанием p, в этой же системе будут получены и искомые коэффициенты – bi, поэтому их необходимо записать d-ичной цифрой. Чаще всего правило деления используется для перевода целых чисел из десятичной в любую другую СС.
Поэтому, правило перевода целых чисел из p-ичной в d-ичную систему средствами p-ичной арифметики, может быть сформулировано: для перевода целого числа Ap из p-ичной системы в d-ичную, необходимо разделить Ap нацело (с остатком) на число d, записанное той же p-ичной СС. Затем, с неполным частным, нужно выполнить ту же операцию и тд, пока последнее неполное частное не станет равно – 0.
Представлением числа Ap в новой СС будет последовательность остатков деления, изображенных d-й цифрой и записанных в порядке, обратном порядку их получения.
Напр.: 7510→(?)16

Г.
§ Перевод правильных дробей.
В это случае, выражение для Ap и Ad, будет выглядеть:


Здесь ai и bi числа p-ичной и d-ичной СС соответственно. Нужно найти известное число в p-ичной системе, выраженное в d-ичной системе. 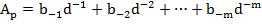
Для определения bi-го умножим обе части равенства на число d, при этом в левой части равенства произведем умножение по правилам p-ичной арифметики и выделим в произведении Apd целую и дробную части:
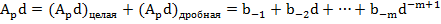

Учитывая, что 0≤bi≤d-1, прировняем между собой целые и дробные последнего равенства. Дробная часть – правильная дробь, в которой можно применить ту же самую процедуру и в результате найти b-2 и тд.
Это повторяем до тех пор, пока дробная часть произведения не станет равна 0 или будет достигнута требуемая точность представления числа в d-ичной СС. Так как все операции выполняются в СС с основанием p, то в этой же системе будут получены и искомые коэффициенты – bi, поэтому их необходимо будет записать d-ичной цифрой. Чаще всего так переводя правильные дроби из десятичной СС в любую другую СС. Таким образом, представление дробной части числа ap в d-ичной системе будет последовательность целых частей полученных произведений, записанных в порядке их получения и изображенных d-ичной цифрой.
Если требуемая точность перевода числа ap – j знаков, то предельная абсолютная погрешность при этом равняется:  .
.
(0,2)10=(?)2 → 0,0011
0,2*2=0,4(0)
0,4*2=0,8(0)
0,8*2=1,6(1)
1,6*2=3,2(1)
Если 0,2 в десятичной системе является точным числом, то при переводе в двоичную получится периодическая дробь. (Apd)=b-1 В данном примере получен период этой дроби.
Особого внимания заслуживает случай перевода чисел из d-ичной в p-ичную, когда основания систем связаны выражением:  , где k-целое положительное число.
, где k-целое положительное число.
В этом случае можно применить следующее правило: в исходной d-ичной записи числа, в переводе из d-ичной в p-ичную, разряды объединяются вправо и влево от точки в группе длинной k. Если нужно, то левее старшей и правее младшей значащих цифр, добавляем нужное количество нулей. Затем каждая полученная группа записывается одной цифрой p-ичной СС.
Для обратного перевода, из p-ичной в d-ичную, каждая цифра числа, записанного в p-ичной системе, заменяется её d-ичным изображением.
1 9 9 6
Напр.: (01 21 21 12)4=(1996)16 (1996)16=(0001 1001 1001 0110)2
§ Двоичная, восьмеричная и шестнадцатеричная СС.
Как отмечалось выше, в вычислительной технике используется двоичная СС. Основной недостаток двоичной системы – быстрый рост числа разрядов при записи больших чисел. Для ЭВМ этот недостаток не существенный.
В случае необходимости кодирования информации в ручную (состояние программы на машинном языке), используют восьмеричную и шестнадцатеричную СС, уменьшая число разрядов. Перевод из одной СС в другую осуществляется достаточно просто в сравнении с десятичной СС.
Чтобы перевести число из двоичной в восьмеричную или шестнадцатеричную, его влево и вправо, от запятой, разбивают на триады (8-ая) и тетрады (16-ая) и каждую полученную группу заменяют соответственной восьмеричной и шестнадцатеричной цифрой.
Напр.: (10101001,10111)2=(010 101 001, 101 110)2=251,568 (1010 1001,1011 1000)2=A9,B816
Правила выполнения арифметических операций (*,/,+,-) в этих СС такие же как и в десятичной, только нужно пользоваться своими, для каждой системы, таблицами сложения и умножения.
§ Двоично-десятичная СС.
Она используется в цифровых автоматах, когда основная часть операций связана не с обработкой и хранением вводимой информации, а с её вводом и выводом на какие-либо индикаторы с десятичным представлением положительных результатов (калькуляторы, кассовые аппараты).
В двоично-десятичной системе десятичные цифры от 0 до 9-и представляются двоичными комбинациями от 0000 до 1001, те двоичным эквивалентом десяти первых 16-тиричных цифр. Преобразование из двоично-десятичной в десятичную систему и обратно, не вызывают затруднения.

Идет прямая замена четырех двоичных цифр одной десятичной или наоборот. Две двоично-десятичные цифры составляют 1 байт, таким образом, с помощью 1-го байта, в двоично-десятичной системе можно представить числа от 0 до 99, а не от 0 до 255, как при использовании восьмиразрядного двоичного числа. Используя 1 байт для представления каждых двух десятичных цифр, можно формировать двоично-десятичные числа с любым требуемым числом десятичных разрядов.
Напр.: пусть имеем число – 1001 0101 0011 1000,
-при рассмотрении его, как двоичное – его десятичный эквивалент будет: ()2→(38200)10
-при рассмотрении его, как двоично-десятичное – ()2-10→(9538)10, что в несколько раз меньше.
Сложение двоично-десятичных чисел, имеющих один десятичный разряд, выполняется так же, как и сложение четырехразрядных двоичных чисел без знака за исключением случая, когда результат превышает величину 1001.
В этом случае необходимо производить коррекцию, которая осуществляется прибавлением к положительному результату двоичного кода числа 6 (0110). Если первоначальное двоичное сложение или прибавление корректировки числа приводит к возникновению переноса, то при сложении многоразрядных двоично-десятичных чисел – перенос осуществляется в следующий десятичный разряд.

1 14
Г.
§ Представление числовой информации в цифровых автоматах.
Информация в памяти ЭВМ записывается в форме цифрового двоичного кода. Для этого в ней имеются ячейки памяти и регистры для хранения двоичной информации. Большинство ячеек имеют одинаковую длину n, для хранения n-бит двоичной информации.
Информация, хранящаяся в такой ячейке, называется словом, состоящим из 1 байта информации. На рисунке представлено двоичное слово, состоящее из 2-х байт.

Каждая ячейка памяти – элемент памяти, который может находится в одном из двух устойчивых состояний (конденсатор: заряжен или разряжен; транзистор: открыт или закрыт; высокое или низкое сопротивление электричества; электромагнит: намагничен или размагничен). Одно из таких устойчивых состояний создает высший уровень выходного сигнала, а другой – низкий. Одно принимается за 1, а другое за 0.
Память ЭВМ состоит из конечной последовательности слов, а слова - из конечной последовательности битов. => тк объем представляемой в машине информации ограничен её памятью, то числовая информация представляется с определенной точностью.
В ЭВМ применяют две формы представления двоичных чисел:
-естественная (с фиксированной точкой);
-нормальная (с плавающей точкой).
В форме с фиксированной точкой все числа изображаются в виде последовательности цифр с постоянным, для всех чисел, положением точки, отделяющей целую часть от дробной.
В этом случае разрядная сетка ЭВМ выглядит так:

Если в результате какой-либо операции получится число, выходящее за допустимый диапазон, то происходит переполнение разрядной сетки, что нарушает нормальную работу машины.
В современных ЭВМ естественная форма представления чисел используется как вспомогательная и только для целых чисел. С плавающей точкой каждое число изображается в виде двух групп цифр.
Первая – называется мантиссой, а вторая – порядком.
Причем абсолютная величина мантиссы должна быть меньше единицы, а порядок должен быть целым числом.
В общем случае число с плавающей запятой можно записать:
 |M|<1 S→целое
|M|<1 S→целое
Такая нормальная форма представления является основой.
§ Выполнение арифметических операций над целыми числами.
Целые числа в ЭВМ, представляются без знака и со знаком.
Целые числа без знака обычно занимают в памяти мантиссы 1 или 2 байта.
Для одного байта - диапазон: 0 … 255;
Для двух байт - диапазон: 0 … 65535 (0 … 216-1)
Целые числа со знаком.
Такие числа обычно занимают в памяти 1,2,4 байта.
Диапазоны: для: 1 байта: -128…+127 (-27…27-1)
2 байт: -215…+215-1
4 байта: -231…231-1
Применяются 3 формы кодирования целых чисел со знаком, а именно: прямой, обратный и дополнительный коды.
§ Прямой, обратный и дополнительный коды.
§ Прямой код.
Прямой n-разрядный двоичный код отличается от двоичного тем, что в нем отводится (как правило, самый старший) один раздел для знака, а остается n-1 разрядов для записи значащих цифр.
При нулевом знаковом разряде – число положительно, при единице – отрицательно. Для прямого кода справедливо следующее соотношение:

, здесь n – разрядность кода, aЗН – значение знакового разряда.
Напр.: имеется число 11012→прямой код. Тогда его десятичная запись будет выглядеть:

§ Дополнительный код.
Использование чисел со знаком (прямого кода) усложняет структуру ЭВМ, тк в этом случае операция сложения 2-х чисел с разными знаками должна быть заменена операцией вычитания меньшего из большего и присвоению результату знака большей величины. Поэтому в ЭВМ, как правило, отрицательные числа представлены в виде дополнительного ил обратного кода, что при суммировании 2-х чисел с разными знаками, позволяет заменить вычитание на обычное сложение, чем упростить конструкцию арифметико-логического устройства ЭВМ.
Суть перевода отрицательных чисел из прямого в дополнительный и обратный коды, заключается в следующем (на примере десятичных чисел):
Пусть машина оперирует с двухразрядными десятичными числами и нужно сложить два числа:
x1=84 x2=-32. Заменим код отрицательного числа его дополнением до 100.
Xдополнит=100-32=68
Сложив первое число с полученным дополнением, получим 152. С учетом того, что ЭВМ работает с двумя десятичными разрядами, конечный результат будет – 52. Равенство полученного результата истинному значению объясняется тем, что при формировании дополнительного кода к x2 мы прибавляем 100, а затем эту сотню вычитаем отбрасыванием частного старшего разряда.
Г.
Операция вычитания сотни заключается в том, что не учитывается код троичного десятичного разряда. Таким образом дополнением M, n-разрядного целого числа K, называют разность:
M=pn-k, где p-основание СС, n-длинна разрядной сетки.
Тк количество n-разрядных целых чисел равно pn→(от 0 до p-1), то ½ этих чисел рассматривают, как положительные от 0 до pn/2-1, а другую половину – как отрицательные, те дополнение к первой половине чисел.
Полный же набор таких чисел называют числами, представленными в дополнительном коде.
Дополнение числа можно получить и без вычитания.
Перепишем выражение для M следующим образом:

, где (pn-1) – состоит из n-цифр (p-1), те старших цифр используемой СС.
Напр.: для пяти разрядных десятичных чисел – это 99999, для четырех разрядных шестнадцатеричных – ffff, для восьми разрядных двоичных – 11111111.
Поэтому [(pn-1)-k] можно получить путем обрабатывания дополнений до (p-1) для каждой из цифр числа k в отдельности, а искомое дополнение получается суммированием этого числа с единицей, тк в двоичной системе дополнение цифр до единицы соответствует их инверсным значениям, то получается простое правило получения дополнения двоичных чисел:
1. получить инверсию заданного числа;
2. обработать дополнительный код заданного числа путем добавления (прибавления) единицы к инверсии этого числа [потом надо не забыть ёё вычесть из пол-ся числа, а затем инвертировать его].
Проверка правильности результата: сумма исходного числа и его дополнительного кода должна быть равна 0 (перенос единицы из старшего разряда не учитывается). Старший бит дополнительного кода двоичных чисел выполняет функцию знака числа (0-для положительных, 1-для отрицательных).
Пи этом положительные числа в дополнительном коде изображается так же, как и в прямом (двоичными кодами с 0 в знаковом разряде). Для дополнительного кода справедливо следующее выражение:

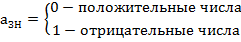
§ Обратный код.
Для представления отрицательных чисел также используется обратный код, который получается инвертированием всех цифр двоичного кода абсолютной величины числа, при этом, необходимо помнить, что все операции с отрицательными числами выполняются в формате машинного слова. Это значит, что к второму числу слева дописываются нули до нужного количества разрядов.
Напр.: для числа -1 и восьми разрядной двоичной сетки, код модуля будет: 00000001, а обратный код будет: 11111110.
Код модуля: 0111 1111 -|127|
Для обратного кода характерно следующее выражение:

Для положительных чисел aЗН=0, и представление числа полностью соответствует с прямым и дополнительным кодами, таком образом сложение числа в прямом, обратном и дополнительном кодах изображается одинаково: двоичными кодами с цифрой 0 в знаковом разряде.
Обычно отрицательные десятичные числа, при вводе в машину, автоматически преобразовываются в обратный или дополнительный двоичный код и в таком виде хранятся, перемещаются и участвуют в различных операциях.
При выводе таких чисел происходит обратное преобразование в отрицательные десятичные числа.
§ Выполнение арифметических операций.
При сложении 2-х чисел: x и y, имеют место четыре основных и два особых случая:
1. (x и y)>0 – при суммировании складываются все разряды, включая разряд знака, тк знаковые разряды положительных разрядов – 0, но сумма равна нулю. 3+7=10
| 0 000 0011 |
| +0 000 0111 |
| 0 000 1010 |
| 0 000 0011 |
| +1 111 0101 |
| 1 111 1000 |
2. x>0; y<0; |y|>|x| 3+(-10)=-7
Обратный код числа (-10)→1111 0101, тогда →обратный код(-7).
Получен корректный результат в обратном коде. При переводе в прямой код, биты цифровой части инвертируются, в результате получаем: -7.
| 0 000 1010 |
| +1 111 1100 |
| 0 000 0110 |
| + 1 |
| 0 000 0111 |
3. x>0; y<0; |y|<|x| 10+(-3)=7 ← обратный код (-3)
← +7
Машина использует полный первоначально не корректный результат, переносом единицы из знакового разряда в младший разряд суммы.
| 1 111 1100 |
| +1 111 1000 |
| 1 111 0100 |
| + 1 |
| 1 111 0101 |
4. x<0; y<0; (-3)+(-7)=-10
Полный первоначально не корректный результат, машина преобразует (исправляет) переносом единицы из знакового разряда в младший разряд суммы.
При переводе разряда в прямой код, биты цифровой части числа инвертируются.
При сложении может возникнуть ситуация, когда старшие разряды результата операции не помещаются в отведенную для него область памяти (переполнение разрядной сетки формата числа).
Для обнаружения переполнения и оповещения о возникшей ошибке, в машине могут быть использованы специальные средства.
Рассмотрим два случая:
| 0 100 0001 |
| +0 110 0001 |
| 0 010 0010 |
1. (x и y)>0 
65+97=162(10100010)
| 1 100 0000 |
| +1 010 0000 |
| 0 110 0000 |
В положительном результате выделенный 0-переполнение, тк семи разрядов цифровой части цифрового разряда не достаточно для размещения восьми разрядной суммы, поэтому старший разряд суммы оказывается в знаковом разряде, но это вызывает несовпадение знаков слагаемых и знака результата, что является свидетельством переполнения разрядной сетки.
2. x<0; y<0; |x|+|y|≥2n-1 -63-95=-158
Здесь знак тоже не совпадает со знаками слагаемых, что свидетельствует о переполнении разрядной сетки.
§ Сложение дополнительных кодов.
Здесь тоже имеют место 6 выше рассмотренных случаев.
| 0 000 0110 0011 1010 |
| +0 100 0100 1001 1011 |
| 0 100 1010 1101 0101 |
x и y – шестнадцати разрядные машинные слова.
1. Пусть x=1594; y=17563; ∑=19157; x>0; y>0; x+y≤215
2. x=1594; y=-17563; ∑=-15969; x>0; y<0; |y|>|x|
| 0 000 0110 0011 1010 |
| +1 011 1011 0110 0101 |
| 1 100 0001 1001 1111 |
3. x=17563; y=-1594; ∑=15469; x>0; y<0; |x|>|y|
| 0 100 0100 1001 1011 |
| +1 111 1001 1100 0110 |
| 0 011 1110 0110 0001 |
Результат корректный, перенос из старшего разряда не учитывается.
4. x=-1594; y=-17563; ∑=-15969; x<0; y<0; |x|+|y|<215
| 1 111 1001 1100 0110 |
| +1 011 1011 0110 0101 |
| 1 011 0101 0010 1011 |
Результат корректный, тк перенос из старшего разряда не учитывается.
5. x=17563; y=-19157; ∑=-28816; x>0; y>0; |x|+|y|>215
| 0 100 0100 1001 1011 |
| +0 100 1010 1101 0101 |
| 1 000 1111 0111 0000 |
При сложении 2-х положительных чисел получается отрицательный результат за счет переполнения разрядной сетки.
&nbs
| <== предыдущая | | | следующая ==> |
| Отказ от вредных привычек | | | Обязанности сотрудника полиции |
Date: 2016-07-22; view: 708; Нарушение авторских прав