
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Поле заряженной бесконечной плоскости
|
|
БИЛЕТ 1
. Электричество – слово древнегреческого происхождения. Еще в VI в. до н.э. Фалесу из Милета было известно, что к янтарным украшениям, надетым поверх шерстяных хитонов, притягиваются легкие пылинки.
Янтарь у греков назывался электрон. Со временем процесс натирания тел шерстью, в результате чего тела приобретали способность притягивать легкие частицы, стали называть электризацией трением. Возникло представление, что при натирании тел на них накапливается некий электрический заряд. Чем больше заряд на теле, тем с большего расстояния и более тяжелые пылинки может оно притягивать.
Позже выяснилось, что само трение не играет существенной роли в электризации. Электризация происходит при контакте любых, чем-либо различающихся тел, причем электризуются оба тела. На них появляются равные по величине электрические заряды противоположного знака.
Современная физика словом электричество обозначает совокупность явлений, обусловленных существованием, движением и взаимодействием электрически заряженных тел или частиц.
2. Электромагнитное поле (ЭМ-поле). Взаимодействие электрических зарядов осуществляется, по современным представлениям (теория близкодействия), с помощью материальной среды, окружающей их, - электромагнитного поля. В системах отсчета, в которых заряженные частицы покоятся, ЭМ-поле вырождается в частный случай – электростатическое поле. Если же заряженные частицы движутся, то наряду с электрическим возбуждается магнитное поле. Последнее может создаваться не только движущимися электрическими зарядами, но также изменяющимся электрическим полем. А электрическое поле, в свою очередь, может создаваться изменяющимся магнитным полем.
Электромагнитное поле – это определенная форма материи, осуществляющая взаимодействие между зарядами. Электрические заряды не существуют в чистом виде, а связаны с частицами, которые имеют отличную от нуля массу покоя. Кванты электромагнитного поля – не имеют массы покоя.
Электромагнитные явления описываются классической электродинамикой, в основе которой лежат уравнения Максвелла.
3. Электромагнитное взаимодействие. Законы классической теории электричества охватывают огромную совокупность электромагнитных процессов. Среди 4-х типов взаимодействий – электромагнитных, гравитационных, сильных, слабых, существующих в природе, электромагнитные занимают первое место по широте и разнообразию проявлений. Это связано с тем, что все тела построены из электрически заряженных частиц, взаимодействия между которыми, с одной стороны, на много порядков интенсивнее гравитационных и слабых, а с другой – являются дальнодействующими в отличие от сильных взаимодействий.
Строение атомных оболочек, сцепление атомов в молекулы и образование конденсированного состояния веществ определяются электромагнитным взаимодействием.
4. История развития учения об электричестве включает в себя три этапа: этап накопления опытных фактов, этап развития учения об электромагнитном поле, этап развития атомистической теории электричества.
а. Этап накопления опытных фактов продолжался с древности до 1-й трети XIX века. За это время были открыты электризация тел трением, существование природного магнетизма, и изобретены приборы для получения и измерения электричества – электрофор, электрофорные машины, электрометры, конденсаторы. К концу XVIII века были открыты основные законы электростатики.

| Рис.52 |
Заканчивается 1-й этап работами М.Фарадея, открывшего законы электромагнитной индукции и электролиза и отчетливо высказавшего идею электромагнитного поля.
б. Этап развития учения об электромагнитном поле, начавшись с М.Фарадея, продолжается до конца XIX столетия. В это время появляется представление об электромагнитном поле как форме материи, как физической реальности, осуществляющей перенос взаимодействия между зарядами. В 60-х годах XIX века Дж.Максвелл, обобщив опытные законы учения об электричестве, создал единую теорию электромагнитного поля. Выяснилось, что изменяющееся электрическое и магнитное поля распространяются с конечной скоростью, равной скорости света. Открытие радио в конце XIX века завершает второй этап.
в. Этап развития атомистической теории электричества начинается с последней трети XIX века и продолжается до наших дней. В это время представление об электричестве как невесомой жидкости меняется на представление, что электрический заряд есть совокупность дискретных электрически заряженных частиц, из которых построено вещество. Изучаются законы движения атомов электричества – ионов и электронов в металлах, в вакууме, в газах, в электролитах. Развивается электронная теория вещества, теория строения атома, ядра и элементарных частиц.
5. Практическое применение электричества в современном мире огромно. Оно определяет технический уровень современной земной цивилизации. Во-первых, электричество – то высокотехнологичный носитель энергии. Наряду с крупными стационарными источниками электрической энергии – электростанциями, чьи энергосети охватывают весь земной шар, широко используются автономные источники – аккумуляторы, «сухие элементы», солнечные батареи и др. Во вторых, электричество – это средства связи: телеграф (с 30-х г.г. XIX в.), телефон (80-е г.г. XIX в.), радио (конец XIX в.). И в третьих, электричество – это средства хранения и переработки информации.
Тепловая мощность тока. Закон Джоуля-Ленца. При перемещении единичного заряда электрическими силами по цепи совершается работа, равная ЭДС источника. Если перемещаемый заряд равен q то работа его перемещения A = E q = E It = I 2(R + r) t (8.14)
Эта работа состоит из двух частей: работы во внешней части цепи I 2 Rt и работы во внутренней части I 2 rt. Работа во внешней части называется полезной.
Полезная мощность Р, выделяющаяся во внешней части цепи, с учётом закона Ома для участка цепи может быть предусмотрена формулами: P = I2R = IU = U2çR (8.15)
Очевидно, формулы (8.15) позволяют вычислить электрическую мощность, выделяющуюся не только во всей внешней цепи, но и на любом элементе цепи, если из группы параметров I, R, U известны любые два.
Если бы заряды двигались в вакууме, то работа А пошла бы на увеличение скорости их движения, A→E кин.При движении зарядов в проводнике скорость направленного движения зарядов практически не изменяется во времени, поскольку в противном случае происходило бы перераспределение концентрации зарядов по проводнику. Получается, что под действием постоянной электрической. силы заряды в проводниках дрейфуют с постоянной скоростью. Это напоминает движение частиц в вязкой среде. Следовательно, работа электрических сил идет на преодоления "вязкого сопротивления" проводника направленному движению зарядов и должна поэтому выделяться в виде тепла.
Количественную связь между выделяющимся в проводниках теплом Q на сопротивлении R и током I нашли опытным путем Джеймс.Джоуль (1841, индукционный метод) и Эмилий Ленц (1844, нагревание спирали) Q = I 2 Rt = IUt =  (8.16)
(8.16)
Связь между единицами тепловой мощности тока и напряжения очевидна: Вт = В×А, Дж = Вт×с = В×А×с.
Закон Джоуля-Ленца в дифференциальной форме определяет тепловую мощность, выделяющуюся в единице объема проводника.
Если по проводнику с удельной проводимостью g, длинной l и с постоянным сечением S проходит ток I, а на концах проводника напряжение U, то выделяющаяся в единице объёма проводника тепловая мощность равна  (8.17)
(8.17)

| Пк U»10кВ d Ra, 0,2 г М − Рис.1 |
Разветвленные цепи. Вычисление взаимодействий. Разветвлёнными называются цепи, содержащие узлы - точки, в которых содержится более трёх проводников. В простейшем случае разветвлённая цепь содержит один источник тока и группу сопротивлений. Поэтому задача сводится к вычислению сопротивлений отдельных участков цепи и всей цепи в целом. Исходными для вычисления являются правила:
а) Сопротивление участка цепи из последовательно соединенных проводников равно сумме сопротивлений этих проводников  .(8.18)
.(8.18)
б) Проводимость участка цепи из параллельно соединённых проводников равна сумме проводимостей этих проводников  или
или  . (8.19)
. (8.19)
Вся работа в дальнейшем сводится к разбиению цепи на такие однородные участки и подсчёту их сопротивлений. Схемы цепей полезно видоизменять, например, делая их более наглядными (рис.52-а), разделяя параллельные ветви в точках одинакового потенциала (рис.52-б), выбрасывая сопротивления, соединяющие эквипотенциальные точки и не вносящие вклада в проводимость цепи (риc.52-а и 52-в),
рассекая цепь эквипотенциальными плоскостями на последовательные участки, состоящие из параллельно включенных сопротивлений (рис52-г).
Если все сопротивления на схеме (рис.52-а) одинаковы и равны R, то сопротивления цепи между точками A и B RАВ = R.
Если на остальных рисунках каждый прямой отрезок между узла-ми на схеме имеет сопротивление R, то на рис.52-б_ RАВ = 4 Rç 5. На рис.52-в RАВ = 6 Rç 7, на рисунке 52-г. RАВ = Rç 2 + Rç 4 + Rç 6 + Rç 6 + Rç 4 + Rç 2 = 11 Rç 6.
БИЛЕТ 2
1. Электростатика – раздел теории электричества, изучающий взаимодействие неподвижных друг относительно друга электрических зарядов. Основные понятия – электрический заряд и электростатическое, то есть не изменяющееся во времени электрическое поле. Источником электростатического поля является электрические заряды. Без электрических зарядов электростатическое поле не существует.
Основные законы электростатики были открыты в XVIII и XIX столетиях. Они выполняются достаточно строго также в тех случаях, когда заряды двигаются друг относительно друга со скоростями, много меньшими скорости света в вакууме.
К основным законам электростатики относятся закон существования двух родов электрических зарядов, закон сохранения заряда, закон квантованности электрических зарядов, закон Кулона.
2. Закон существования двух родов электрических зарядов. В 1733 г. француз Шарль Дюфе установил, что «существуют два рода электрических зарядов – стеклянное и смоляное. Разноименные заряды притягиваются, одноименные – отталкиваются».
Смоляное электричество появлялось на янтаре, а стеклянное – на стекле, на драгоценных камнях, на шерсти животных. В 1747 г. американец Бенджамин Франклин предложил называть стеклянное электричество положительным и обозначать знаком «+» (плюс), а смоляное – отрицательным и обозначать знаком «–» (минус).
При соприкосновении всегда электризуются оба тела. В паре эбонит+мех эбонит электризуется отрицательно, мех – положительно. В паре металл+шерсть металл заряжается отрицательно, шерсть – положительно. В паре металл+каучук металл электризуется положительно, каучук – отрицательно. Основными носителями положительных зарядов являются протоны, отрицательных – электроны.
3. Закон сохранения электрического заряда. Он был осознан по совокупности физических фактов в XVIII веке. Алгебраическая сумма электрических зарядов любой изолированной (или замкнутой) системы остается постоянной, какие бы процессы не происходили внутри этой системы. Полный заряд такой системы есть релятивистский инвариант. Его величина не зависит от выбора системы отсчета и от скорости движения зарядов. Изолированной считается здесь такая система, через границы которой не проникает вещество. Свет может входить и выходить из системы.
Вначале закон сохранения заряда был открыт по аналогии с законами сохранения импульса и механической энергии. Поэтому он мог рассматриваться как постулат, которому подчинялись без исключения все электрические опыты. Начиная с XX в. после наблюдения актов аннигиляции частиц с античастицами (электрон+позитрон) закон сохранения заряда может считаться уже эмпирическим законом, доказанным прямым экспериментом.
4. Закон квантованности (дискретности) электрических зарядов (XIX в.). Делимость электрических зарядов ограничена неким минимальным зарядом e, называемым элементарным. Зарядов, меньших элементарного, в природе нет. Положительный e+ и отрицательный e– элементарные заряды равны по абсолютной величине, |e+|=|e–|.
Идея дискретности электрических зарядов появилась после опытов Майкла Фарадея по электролизу (1834 г.). Из них следовало, что количество отложившегося на электродах вещества во всех случаях пропорционально величине электрического заряда, прошедшего через электролит. Этот факт можно объяснить лишь тем, что каждая отложившаяся на электроде частица вещества переносит одну и ту же порцию электрического заряда.
В 1881 г. Герман Гельмгольц сделал такую оценку, а Джозеф Томсон в 1897 г. в опытах с катодными лучами подтвердил идею существования атомов электричества – электронов и измерил их удельный заряд. Абсолютную величину элементарного заряда впервые определил с высокой точностью в 1909 г. американец Роберт Милликен.
Схема одного из вариантов установки Милликена показана на рис.1.
Сквозь отверстие O в верхней пластине горизонтально расположенного плоского воздушного конденсатора внутрь него попадали капельки распылявшегося масла. Под действием ионизирующего излучения источника S (препарат радия в свинцовом контейнере) капельки могли приобретать и терять электрический заряд.
Если на конденсатор подать напряжение U, то из множества капель в поле зрения микроскопа М можно выделить ту, которая движется кверху со скоростью, приемлемой для визуального наблюдения. Раз капля движется вверх, то это значит, что она имеет некоторый заряд q. Измерения выполнялись так:
а.Пластины конденсатора замыкались между собой накоротко (переключатель Пк ставился в левое по рис.1 положение). Электрическое поле в конденсаторе исчезало. Капля под действием силы тяжести падала равномерно вниз со скоростью v 1. Сила тяжести  уравновешивалась силой вязкого сопротивления воздуха FS 1 (рис.2-а). Уравнение движения капли в проекции на вертикальную ось ОY имеет вид: mg + FS 1 = 0.(2.1)
уравновешивалась силой вязкого сопротивления воздуха FS 1 (рис.2-а). Уравнение движения капли в проекции на вертикальную ось ОY имеет вид: mg + FS 1 = 0.(2.1)
б. На конденсатор подавалось напряжение U (переключатель Пк ставился в правое по рис.1 положение). Капля начинала двигаться вверх в электрическом поле напряжённостью E=U| d со скоростью v 2 (рис.2-б). Уравнение движения капли в проекции на ось Y имеет вид: –mg–FS 2 +qE =0.(2.2)
Так как FS 1 = 6 πhrv 1, а FS 2 = 6 πhrv 2, где h – вязкость воздуха, а r – радиус капли, то система уравнений принимает вид:
 (2.3)
(2.3)
Разделив 2-е уравнение на 1-е, получаем заряд капли  (2.4)
(2.4)
Милликен наблюдал некоторые капли в течение нескольких десятков минут, многократно поднимая их вверх, измеряя скорость подъема v 2, а затем измеряя скорость v 1 опускания капли.
Если напряжение U на конденсаторе не менять, то коэффициент перед скобкой остается постоянным. Поэтому при перезарядке капли в случае дискретного изменения заряда q скорость подъёма капли должна изменяться тоже ступенчато.
Для вычисления абсолютного заряда капли нужно из формулы (2.4) исключить ее вес. Это можно сделать, используя режим свободного падения капли с плотностью ρ. Так как mg = (4 πr 3 | 3 )ρg = 6 πhrv 1, то, выразив отсюда радиус капли  и подставив его в выражение веса капли, получаем:
и подставив его в выражение веса капли, получаем:  и
и  (2.5)
(2.5)
В итоге всех экспериментов после исследования тысяч капель Милликен нашел величину минимального заряда. Его современное значение составляет
e = (1,6021892±0,0000046)·10−19 Кл.
Опыты, выполненные в 60-е годы XX в. с атомными пучками цезия и с молекулярным водородом, показали, что отрицательный и положительный элементарные заряды если и отличаются по абсолютной величине между собой, то не более чем на 10−20 e.
В макроскопической электростатике дискретность зарядов не имеет практического значения. Дифференциальные объемы заряженных тел обычно содержат огромное количество элементарных зарядов. Это позволяет считать изменение зарядов непрерывным.
Однако в строении материи и в физическом портрете Вселенной дискретность зарядов играет решающую роль.
Разветвленные цепи. Правила Кирхгофа. В разветвленных электрических цепях, содержащих несколько источников тока, в разных участках, вычисление токов становится сложной задачей. Эти вычисления сильно упрощаются и формализуются, если пользоваться алгоритмом Кирхгофа, сформулированным им в идее двух правил:
1-е. Сумма токов в узле равна нулю  . (8.20)
. (8.20)
2-е. Сумма падений напряжений в контуре равна сумме действующих в контуре ЭДС.  (8.21)
(8.21)
Контуром называется кольцевой участок цепи. Первое правило выражает закон сохранения электрического заряда, второе закон Ома для замкнутой цепи.
При решении задач произвольно задается направление токов и произвольно выбирается направление обхода в контурах. В качестве примера рассмотрим технологию вычисления токов в ветвях цепи, показанной на рисунке (рис.53).
Полагаем значения всех сопротивлений и ЭДС всех источников тока известными.
Токи, идущие вдоль направления обхода, принимаются положительными, против - отрицательными. ЭДС, действующие в направлении обхода, также считаются положительными, а против - отрицательными.
Чтобы задача могла быть решена, общее число уравнений должно быть равным числу неизвестных токов. В начале составляются уравнения для узлов. Число независимых уравнений для токов в узлах на одно меньше количества узлов. Остальные недостающие уравнения составляются для контуров. Их число равно числу внутренних областей плоской схемы без взаимопересечений ветвей. Целесообразно в первую очередь составить уравнения для внутренних контуров, то есть минимальных. В схеме цепи на рис.53 уравнение для узлов должно быть одно. Полагаем токи, входящие в узел, положительными, выходящие - отрицательными. Тогда, например, для узла 1: I 1 - I 2 - I 3 = 0 (8.22)
Всего неизвестных токов три, поэтому нужны ещё два уравнения. Составим их для внутренних контуров 1 и 2.
Контур 1: I 1 R 1+ I 2 R 2 = E 1 - E 2 (8.23)
Контур 2: I 2 R 2+ I 3 R 3 = E 2 - E 3 (8.24)
Итак, имеем систему из трёх линейных уравнений с тремя неизвестными I 1, I 2, I 3.
В принципе неизвестными могут быть и другие величины. Но для получения однозначного решения число неизвестных параметров должно быть равно числу независимых уравнений.
Напомним, что направление токов и обхода произвольны. Если какой-либо ток в решении окажется отрицательным, это значит, что его действительное направление противоположно в начале принятому.
БИЛЕТ 3
. Электрическое поле. Это понятие ввел Майкл Фарадей в середине XIX века. Начиная с Фарадея, физика стала рассматривать электрическое поле как особую форму материи, способную переносить действие одного заряда на другой.
Кванты электромагнитного поля не имеют массы покоя, но обладают энергией и импульсом (момпентом импульса).
Источником электромагнитного поля являются электрические заряды. Для измерения и описания поля, созданного неким зарядом Q, нужен еще один заряд q, который можно было бы вносить в разные точки поля заряда Q. Этот вспомогательный заряд q называют пробным. Предполагается, что пробный заряд всегда положителен, а его величина много меньше заряда Q.
2. Напряженностью электрического поля  называют физическую величину, равную отношению силы
называют физическую величину, равную отношению силы  ,действующей на пробный заряд q, к величине этого пробного заряда.
,действующей на пробный заряд q, к величине этого пробного заряда.  (3.1)
(3.1)
Фарадей предложил графически изображать электрические поля непрерывными силовыми линиями или линиями напря-женности, в каждой точке которых вектор силы  или напряженности
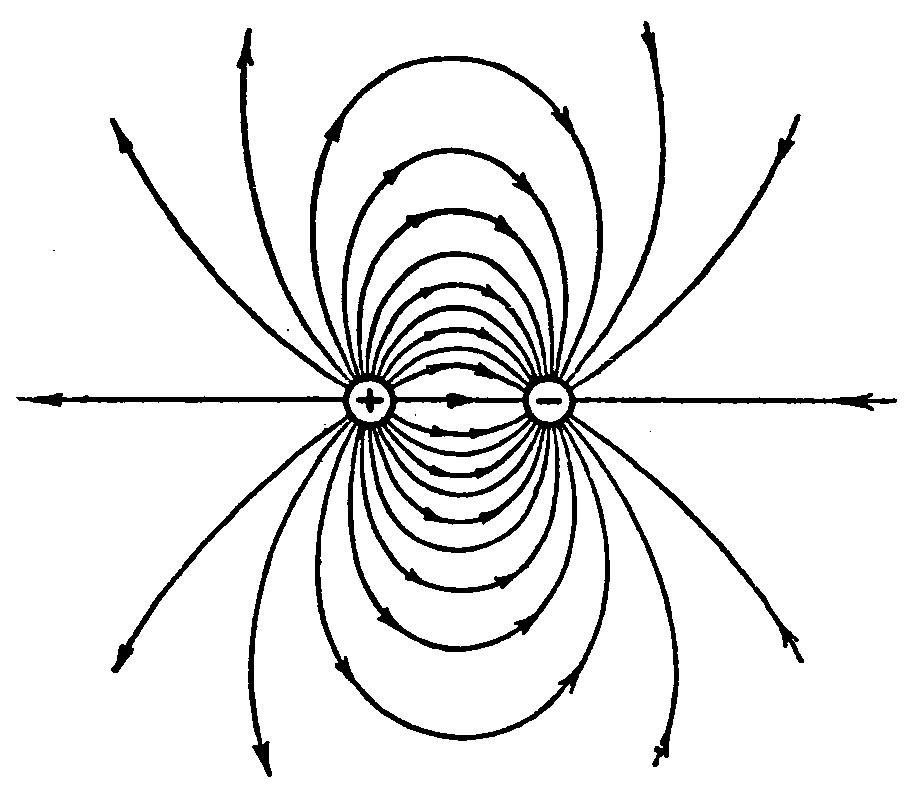
или напряженности  направлены по касательной к ним. Все линии начинаются на положительных и заканчиваются на отрицательных зарядах. Если поле создается уединенным зарядом Q, то линии уходят на бесконечность. Чем больше заряд Q, тем больше линий выходит из него или заканчивается на нём.
направлены по касательной к ним. Все линии начинаются на положительных и заканчиваются на отрицательных зарядах. Если поле создается уединенным зарядом Q, то линии уходят на бесконечность. Чем больше заряд Q, тем больше линий выходит из него или заканчивается на нём.
3. Поле точечного заряда. Пусть электрическое поле создается уединенным точечным зарядом Q. Чтобы измерить его в некоторой точке, надо внести в эту точку пробный заряд q. Сила  действия поля на заряд q по закону Кулона
действия поля на заряд q по закону Кулона  (3.2)
(3.2)
Здесь  –радиус вектор, проведенный из точечного заряда Q в ту точку поля, где находится пробный заряд q (рис.6-а).
–радиус вектор, проведенный из точечного заряда Q в ту точку поля, где находится пробный заряд q (рис.6-а).
Напряженность поля создаваемого зарядом Q, равн  (3.3)
(3.3)
Поле уединенного точечного заряда обладает центральной симметрией. На рис.6-б показаны линии  поля положительного точечного заряда Q, лежащие в плоскости проходящей через заряд Q. Линии направлены от центра к периферии. Линии поля отрицательного заряда направлены от периферии к центру (рис.6-в).
поля положительного точечного заряда Q, лежащие в плоскости проходящей через заряд Q. Линии направлены от центра к периферии. Линии поля отрицательного заряда направлены от периферии к центру (рис.6-в).
Достоинством графической интерпретации поля является не только, возможность оценивать по конфигурации линий направление вектора Е, но и возможность оценивать его величину, поскольку густота линий пропорциональна напряженности Е.
Графическое изображение количественных характеристик электрического поля возможно благодаря тому, что поле Е точечного заряда убывает пропорционально 1 ç r2, и на любом расстоянии от заряда r плотность линий, то есть их число на единицу площади поверхности перпендикулярной силовым линиям убывает также пропорционально 1 ç r2.
4. Суперпозиция электрических полей. Чтобы ответить на вопрос; чему равна напряженность поля, создаваемого несколькими различными точечными зарядами, находящимися в разных местах, надо знать, как складываются поля.
Опыт показывает, что сила взаимодействия любых двух зарядов не зависит от наличия других зарядов. Это значит, что сила, действующая со стороны системы зарядов q 1… q n на пробный заряд q, равна геометрической сумме сил со стороны каждого из них, а напряженность суммарного электрического поля равна геометрической сумме напряженностей полей, создаваемых каждым зарядом в отдельности.  (Закон сложения электрических полей)(3.4)
(Закон сложения электрических полей)(3.4)
Способность электрических полей складываться без взаимных искажений называется принципом суперпозиции это объективное свойство линейных силовых полей, известное нам из механики. Благодаря суперпозиции электрических полей существует возможность рассчёта полей системы точечных зарядов и протяженных заряженных макротел.
5. Примеры рассчёта полей. Рассчитать поле - это значит найти значение вектора Рис 8 напряженности Е в каждой точке поля.
Пример 3.1. Поле двух точечных зарядов. Пусть два заряда q 1 и q 2 находятся на расстоянии 2 а друг от друга. Надо найти напряженность суммарного поля.


| Рис 7 r 1 r 2 j 1 j 2 q 1(- a,0) 0 q 2(+ a,0) x а). Рис.7 |
Напряженность поля в любой точке А с координатами x, y равна сумме напряжённостей (рис.7-а):  (3.5)
(3.5)
Здесь  –поле заряда q 1,
–поле заряда q 1,  –поле заряда q 2, E 1 x и E 2 x – проекции векторов
–поле заряда q 2, E 1 x и E 2 x – проекции векторов  и
и  на ось OX, E 1 y и E 2 y – проекции векторов на ось OY,
на ось OX, E 1 y и E 2 y – проекции векторов на ось OY,  и
и  –единичные орты
–единичные орты  этих осей.(3.6)
этих осей.(3.6)  (3.7)
(3.7)
 (3.8) Таким путем можно вычислить поле сколь угодно большего числа точечных зарядов. Достаточно лишь добавить в формулу (3.5) проекции напряжённостей поля следующих зарядов:
(3.8) Таким путем можно вычислить поле сколь угодно большего числа точечных зарядов. Достаточно лишь добавить в формулу (3.5) проекции напряжённостей поля следующих зарядов:
E 3 x, E 3 y, E 4 x, E 4 y и так далее.. Если система зарядов не плоская или не имеет оси симметрии, то задача должна решатся в трехмерном пространстве.

| Рис 12 |
 (формула 9.6), то энергия, отдаваемая электронами в единице объема в течении одной секунда, равна
(формула 9.6), то энергия, отдаваемая электронами в единице объема в течении одной секунда, равна
 (9.9)
(9.9)
Эта энергия выделяется в виде тепла, поэтому формула (9.9) выражает закон Джоуля Ленца в дифференциальной форме. Выражение для удельной проводимости  (9.10)
(9.10)
получилось то же самое, что и в формуле закона Ома (9.8).
Строго говоря, предположение, что электрон отдает всю энергию при столкновении с атомом справедливо лишь тогда, когда атом покоится. Но атомы колеблются, а соударения не являются абсолютно неупругим. Поэтому электроны могут как отдавать энергию (соударение с убегающим атомом), так и получить ее (соударения с набегающим атомом). В статистике в условиях теплового равновесия средняя энергия движения электронов при постоянной температуре остается постоянной.
Но когда электронный газ приобретает направленную скорость дрейфа, он приобретает избыточную над тепловой энергию движения. Эта энергия электронов неравновесная с энергией узлов. Поэтому она непрерывно передается узлам кристаллической решетки, повышая температуру проводника.

| Рис 13 Рис.13 |
 Закон Видемана-Франца. (9.11)
Закон Видемана-Франца. (9.11)
L - коэффициент, одинаковый для всех металлов, его называют числом Лоренца.
Классическая электронная теория так объясняет этот закон.
Поскольку электроны очень подвижны, то можно полагать, что теплопроводность металлов обусловлено в основном теплопроводностью его электронного газа. Его коэффициент теплопроводности равен  (9.12)
(9.12)
Здесь l - средняя длина свободного пробега электронов, u - их средняя скорость теплового движения, i = 3 - число степеней свободы электронов, k постоянная Больцмана.
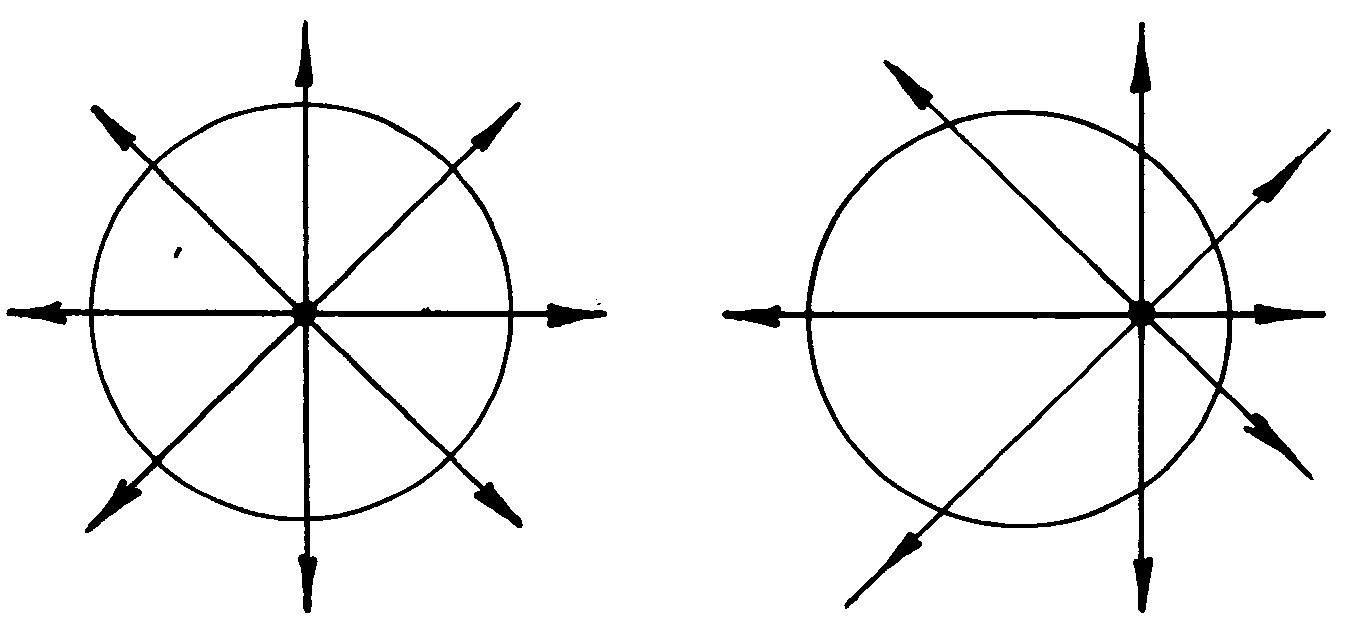
|
Рис.14
 (9.13).
(9.13).
 (9.14).
(9.14).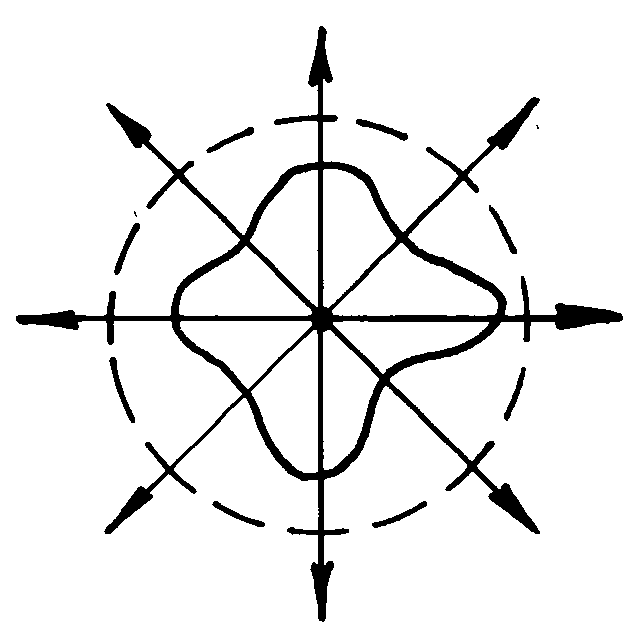
 , то u ~
, то u ~  . Отсюда g = 1 çr ~
. Отсюда g = 1 çr ~  , или
, или  ~
~  . Но опыт дает линейную зависимость удельного сопротивления от температуры,
. Но опыт дает линейную зависимость удельного сопротивления от температуры,  , или r ~ T. Расхождение необъяснимо.
, или r ~ T. Расхождение необъяснимо. (рис.12).
(рис.12). , и мыбудем знать не только протекающий через площадку объем жидкости, но и то, в каком направлении она течет через площадку – по нормали (положительный поток) и против нормали (отрицательный поток).
, и мыбудем знать не только протекающий через площадку объем жидкости, но и то, в каком направлении она течет через площадку – по нормали (положительный поток) и против нормали (отрицательный поток).
 . (4.1)
. (4.1)
 очень плодотворна при вычислении симметричных электростатических полей.
очень плодотворна при вычислении симметричных электростатических полей.
 через всю поверхность этой сферы. Приняв во внимание, что векторы
через всю поверхность этой сферы. Приняв во внимание, что векторы  и
и  сонаправлены,
сонаправлены,  (рис.13).
(рис.13).
 (4.2)
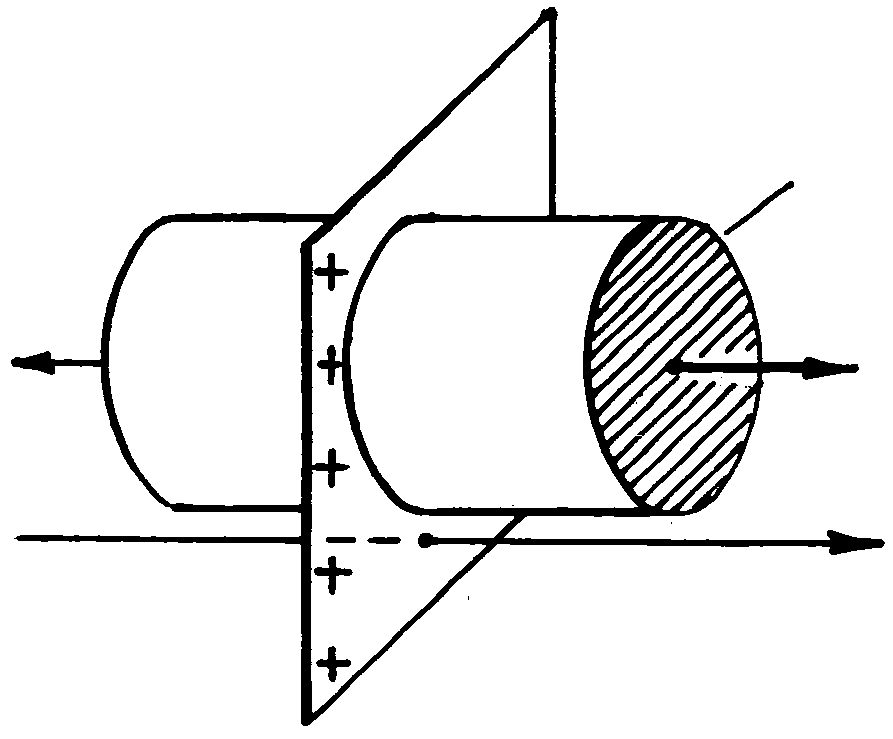
(4.2) . Это видно из того, что любая замкнутая поверхность может быть охвачена сферой. Поскольку линии вектора Е не имеют разрывов, то какой поток N проходит через сферу, таков же он через любую замкнутую поверхность (рис.15).
. Это видно из того, что любая замкнутая поверхность может быть охвачена сферой. Поскольку линии вектора Е не имеют разрывов, то какой поток N проходит через сферу, таков же он через любую замкнутую поверхность (рис.15). (4.3)
(4.3) (4.4)
(4.4)

 (4.5)
(4.5) .Поэтому потенциал всех точек внутреннего пространства сферы одинаков и равен потенциалу самой сферы.
.Поэтому потенциал всех точек внутреннего пространства сферы одинаков и равен потенциалу самой сферы.  при r < R. Итак,
при r < R. Итак,  (4.6)
(4.6)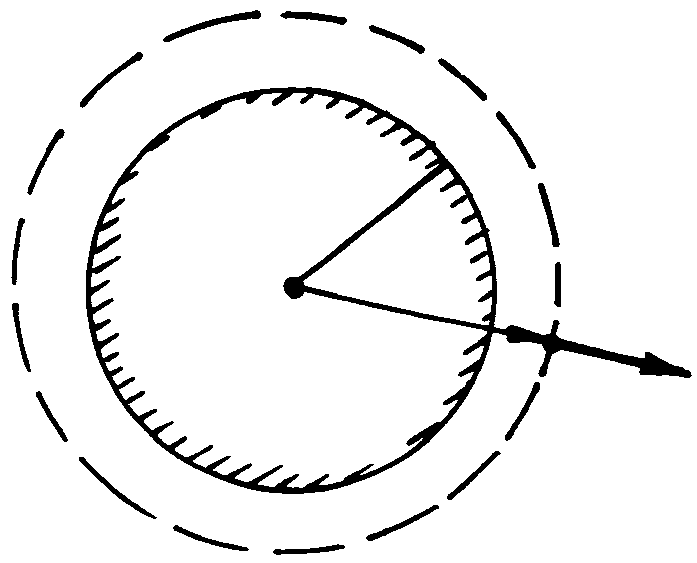

 Рис.17
Рис.17
 (4.7)
(4.7)
 –полный заряд на физической сфере. Отсюда
–полный заряд на физической сфере. Отсюда (4.8)
(4.8)

 Отсюда
Отсюда  (4.11,12)
(4.11,12) (4.13)
(4.13) (4.14)
(4.14) (1.15,16)
(1.15,16)
 на поверхности шара не имеет разрыва (в отличии от заряженной сферы), но ее производная имеет разрыв, меняясь по величине и по знаку. Потенциал и его производная на поверхности шара не имеет разрыва.
на поверхности шара не имеет разрыва (в отличии от заряженной сферы), но ее производная имеет разрыв, меняясь по величине и по знаку. Потенциал и его производная на поверхности шара не имеет разрыва.
 (4.17)
(4.17) Так как
Так как  ,то получаем
,то получаем  . Или в векторной форме.
. Или в векторной форме.  (4.18)
(4.18) ,то
,то  (4.19)
(4.19) , то
, то  (4.20)
(4.20)
 – расстояние между ними вдоль линии поля, равно
– расстояние между ними вдоль линии поля, равно  , (4.21)
, (4.21)





 . Поле внутри проводника исчезает.
. Поле внутри проводника исчезает. , то отсюда следует,
, то отсюда следует,  . Проводник в поле любой формы и напряженности имеет одинаковый по всему объему потенциал. Говорят, объем проводника эквипотенциален.
. Проводник в поле любой формы и напряженности имеет одинаковый по всему объему потенциал. Говорят, объем проводника эквипотенциален.