Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Методы получения случайных чисел с заданным законом распределения
|
|
;
Р2 - проверка условия 
;
К3 – счетчик количества поступивших заявок 
;
Р4 – проверка условия 
- момент освобождения канала от обслуживания (j-1) -й заявки;
Р5 – проверка условия К>0, где К – число занятых мест в очереди;
F6 – формирование момента начала обслуживания заявки 
;
Р7 – проверка условия К<4;
К8 – счетчик количества заявок в очереди К:=К+1;
F9 – запись в ячейку V[K] момента поступления заявки в систему 
;
К10 – счетчик отказов L:=L+1;
Р11 – проверка условия K>1;
F12 – выбор заявки из очереди;
F13 – запись в ячейку V[K] момента поступления в систему (j+ 1)-ой заявки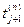 
;
F14 – формирование момента начала обслуживания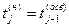 
;
Ф15 – формирование случайного времени обслуживания заявок 
;
А16 – вычисление момента освобождения канала:
;
К18 – счетчик количества обслуженных заявок М:=М+1;
А19 – вычисление длительности ожидания заявки в очереди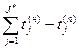 
;
К20 – счетчик количества заявок в очереди;
Р21 – проверка условия J<J*, где J* - наперед заданное количество реализаций;
подразделяются на элементы двух видов: первого рода (а) и второго рода (в). Серией называется любой отрезок последовательности, состоящий из следующих друг за другом элементов одного и того же рода. Число элементов в отрезке называется длиной серии. Обычно к элементам первого рода относят СЧ меньше 0,5, а к элементам второго рода – все остальные.
Введем обозначения:
- число серий элементов Q длиной I в исследуемой совокупности 
;
- число серий элементов b, длиной i:
- общее число серий элементов а;
- общее число серий элементов b;
- максимальная длина серий элементов a и b соответственно;
- общее число серий в исследуемой совокупности РСЧ.
После выделения серий находят теоретические и эмпирические значения величин Ra, Rb, и R по большой выборке, задаваясь некоторой величиной доверительной вероятности 
.
Теоретическое значение 
можно найти по формуле
. (8)
Значения Ra и Rb являются нижними пределами числа серий при заданной величине 
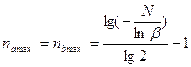. (9)
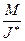, доли заявок, получивших отказ 
и среднего времени нахождения заявки в очереди
;
Я23 – печать результатов, конец.
Операторная схема алгоритма имеет следующий вид:
9,10,19,21Ф1 Р2!5а К3 Р4!7 Р5!11 F615 4Р7!10 К8 F91 7К101
5Р11!13 Ф12 11,12F13 11а,13,20F14 6,14Ф15 А16 Р17!10а К18
А19 12аК2014 2Р5а!21 Р11а!14 Ф12а20 17К10а 5а,10аР21!1 А22
Я23.
Операторы Р5а, Р11а, К10а, Ф12а совершенно аналогичны соответственно операторам Р5, Р11, К10, Ф12. Блок-схема алгоритма приведена на рис.1. Аналогично рассмотренному выше примеру могут быть построены алгоритмы для многоканальных СМО с ожиданием, для которых характерны другие правила построения очереди, свои правила выбора каналов.
(5)
Для функции распределения 
составлены таблицы, пользуясь которыми определяют, удовлетворяет ли проверяемая последовательность случайных чисел данному критерию.
При анализе «равномерности» СЧ критерий Колмогорова используется реже, чем критерий 
2. Это связано с тем, что проверка по критерию Колмогорова требует фиксации всех случайных чисел в памяти машины и их дальнейшего упорядочения в порядке возрастания, что значительно усложняет программу. Для проверки по критерию Пирсона такая процедура не является обязательной.
Проверку «случайности» РСЧ на практике производят методом комбинации или методом серий. С точки зрения реализации на ЦВМ метод серий требует меньшего количества операций и поэтому используется чаще.
Проверка РСЧ методом комбинаций сводится к подсчету единиц (или нулей) в 
испытуемых разрядах двоичного числа 
и вычислению частоты появления 0, 1, 2, ……, единиц (нулей) в контролируемой совокупности объема N. Статистическая частота появления единиц (нулей), полученная в результате испытания по каждому i -му интервалу, сравнивается с теоретической, и вычисляется мера расхождения 
(6)
Затем по таблицам для 
степеней свободы находится величина вероятности, которая и позволяет оценить случайность путем сравнения с некоторым доверительным уровнем. На практике величину N выбирают 
и проверяют все к разрядов 
(7)
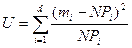, (3)
где mi – тов выборки, попавших в i -тый разряд;
d – количество разрядов, на которые разбивается выборка значений случайной величины.
При 
закон распределения величины U зависит только от числа разрядов d и приближается к так называемому распределению 
с r степенями свободы. Величина r определяется как разность d-S, где S – число наложенных на статистические частоты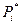 
независимых условий. В качестве таких условий могут выступать: равенство единице суммы статистических частот 
и числу степеней свободы.(табличные значения) находится вероятность того,что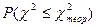 
. Если эта вероятность превышает некоторый доверительный уровень, величина которого выбирается исходя из конкретных условий задачи, то считается что гипотеза о распределении не опровергается опытными данными.
Критерий Колмогорова основан на определении величины
, (4)
которая принимается в качестве меры расхождения. Затем находится величина 
и по таблицам значение вероятности 
. Если 
, то анализируемая гипотеза принимается; в противном случае расхождение между 
и 
следует считать не случайным. Критерий Колмогорова рекомендуется применять в тех случаях, когда известны все параметры теоретической функции распределения.
Критерий 
(1)
, (2)
где N – общее число используемых РСЧ, достаточное для получения заданной точности.
Для принятия или опровержения гипотезы о равномерности выбирается некоторая величина U, характеризующая степень расхождения теоретического и статистического распределений. Величина U может быть выбрана различными способами: в качестве U можно взять сумму квадратов отклонений теоретических вероятностей Pi от соответствующих статистических частот Pi*, максимальное отклонение статистической функции распределения 
, над которой производились опыты, и от числа опытов N.
После проведения эксперимента необходимо сравнить полученную величину расхождения U с теоретической, связанной с недостаточностью статистического материала и другими случайными причинами. Если вероятность того, что 
велика, можно считать, что гипотеза о законе распределения СВ не опровергается опытными данными.
На практике наиболее часто используются критерий Пирсона 
закона распре-деления 
,
где 
- целая часть полученного произведения.
На практике используются несколько разновидностей датчиков Лемера, отличающихся различными значениями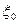 
.
Алгоритм для получения РСЧ по методу Дэвиса имеет вид
Описанные способы получения РСЧ позволяют получить не непрерывную, а дискретную совокупность чисел. Это объясняется тем, что количество разрядов ДСЧ или величина разрядной сетки ЦВМ ограничена.
Такое распределение дискретных равновероят-ных чисел называют квазиравномерным. Дисперсия полученной дискретной СВ отличается от теоретической, однако при достаточно большом числе разрядов это различие можно считать несущественным.