Истечение через малое отверстие в тонкой стенке

Рисунок 3.28 – Истечение из большого резервуара через малое отверстие

Рассмотрим большой резервуар с жидкостью, из которого через малое отверстие в боковой стенке вытекает струйка (рисунок 3.28). Термины «большой резервуар» и «малое отверстие» означает, что эти размеры не сказываются на изменении высоты жидкости (напора) в резервуаре при вытекании из него жидкости. Термин «тонкая стенка» означает, что после сжатия струя вытекающей жидкости не касается цилиндрической поверхности отверстия.

Рассмотрим два сечения в этом резервуаре, обозначенные индексами 0 и С. Запишем уравнение Бернулли для этих условий

Для описанных условий можно считать, что движения жидкости в сечении 0 нет, следовательно, скоростной напор равен нулю. Разницей нивелирных высот, из-за их малого влияния можно пренебречь. Коэффициентом в данном случае обозначено сопротивление отверстия. Этот коэффициент учитывает потери энергии жидкости на сжатие струи и трение в струйках жидкости вблизи отверстии при формировании вытекающей струи. С учетом этого уравнение примет вид

.

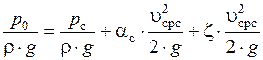После перегруппировки членов получим

.

Выразим отсюда скорость

.

Заменим скорость отношением расхода к площади живого сечения потока и вновь перегруппируем

.

Проанализируем полученное выражение. Заметим, что индекс «с» относится к струе, и это единственный индекс, относящийся к движущейся жидкости «на выходе» рассматриваемого проходного сечения.

Величина - называется коэффициентом скорости. Если считать распределение скоростей в струе равномерным (), а жидкость идеальной, в которой нет потерь на трение, то коэффициент . Тогда коэффициент скорости .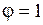

Отсюда становится понятным физический смысл коэффициента скорости. Он выражает отношение действительного расхода через проходное сечение к теоретическому расходу. Действительным расходом называют расход, который на самом деле проходит через проходное сечение. Теоретический расход это такой, который мог бы протекать через проходное сечение при отсутствии потерь.

Учитывая, что , получим

,

где - коэффициент расхода.

Тогда окончательно будем иметь формулу

, или ,

где - разность давлений до проходного сечения и после него.

С помощью полученного выражения решается задача определения расхода для всех случаев течения жидкости под действием разности давлений. Кроме того, из данного выражения видно, что причиной течения жидкости является разность давлений. Жидкость всегда движется из области высокого давления область низкого давления. По существу приведённое выражение можно считать инженерной формой уравнения Бернулли.

При прохождении жидкости через малое отверстие происходит «смятие» струи. На немецком языке «мятие» - «drosseln». Поэтому в технике истечение через малое отверстие называют дросселированием. Гидравлический аппарат, предназначенный для дросселирования, называется дросселем, а отверстие в этом гидроаппарате называется проходным сечением.

Наиболее сложной задачей практического применения этого уравнения является определение коэффициента , значение которого зависит от степени сжатия струи и режима её течения, структуры распределения скоростей вблизи проходного сечения, которая в свою очередь зависит от формы входа в проходное сечение. Этот коэффициент определён экспериментально. Он, как и коэффициенты и , зависит от числа Рейнольдса и эти зависимости можно представить с помощью графика (рисунок 3.29).

На графике буквами Re_т обозначает число Рейнольдса, посчитанное по теоретической скорости, соответствующей теоретическому расходу.

С увеличением скорости истечения и связанным с этим увеличением Re_т коэффициент скорости φ быстро нарастает и при Re_т → ∞ стремится к значению φ =1,0. Это свидетельствует о значительном уменьшении гидравлического сопротивления отверстия за счёт снижения влияния вязкости.

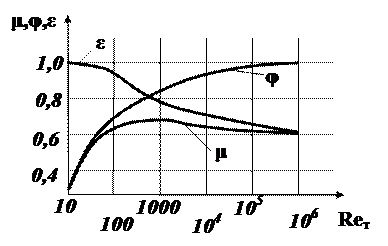
Рисунок 3.29 – Зависимость ε, μ и φ от число Рейнольдса

Коэффициент сжатия струи ε с увеличением Re_т уменьшается и при Re_т → ∞ стремится к значению ε = 0,6.

Коэффициент расхода μ, являясь произведением коэффициентов φ и ε, на первом этапе растёт, достигая максимального значения μ = 0,69 при Re_т ≈ 350, а затем плавно снижается до μ ≈ 0,6.

Таким образом, только за счёт коэффициента μ величина расхода уменьшается на 30 – 40 % относительно теоретически возможного.

Date: 2016-07-18; view: 456; Нарушение авторских прав