
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Обратные траектории движения воздуха
|
|
Пространственный и временной анализ траекторий движения воздушных потоков получил широкое распространение благодаря появлению доступного интернет-сервиса для проведения расчетов с помощью модели HYSPLIT, а также открытого свободно распространяемого программного обеспечения FLEXTRA, предназначенных для моделирования траекторий движения воздушных частиц в атмосфере.
Проведение расчетов как прямых, так и обратных траекторий движения воздушных частиц возможно только при условии свободного доступа к необходимой метеорологической информации, что обеспечивают в настоящее время открытые базы данных реанализа, например, Европейского центра среднесрочных прогнозов погоды и Национального управления океанических и атмосферных исследований США.
Кроме упомянутых выше программных комплексов для расчета обратных траекторий, получивших широкое распространение благодаря своей доступности и гибкости, существуют другие источники, которые представляют собой уже сформированные базы данных, содержащие информацию о динамике атмосферы. На сайте системы аэрозольного мониторинга AERONET, в рамках которой проводятся спектральные фотометрические измерения оптических характеристик атмосферы по всему земному шару (рисунок 1.1), для каждой станции сети доступны обратные траектории движения воздушных потоков.

Рисунок 2.1.[Сергей2] - Схема размещения станций мониторинга глобальной сети AERONET по состоянию на 2014 г.
Траектория движения воздушного потока представляет собой набор точек в пространстве, каждая из которых определяется координатами положения лагранжевой частицы в определенный момент времени. По способу отсчета времени вдоль траектории различают прямые и обратные траектории движения воздуха. Прямая траектория показывает путь, который проходит воздушная частица по мере ее отдаления от точки «старта» траектории. При определении обратной траектории используется отрицательный шаг по времени, т. е. траектория характеризует путь, который прошла воздушная частица до ее прихода в пункт мониторинга. За сутки восстанавливаются две обратные траектории, соответствующие приходу воздушных масс в 0 и в 12 часов по Гринвичу.
На рисунке 1.2 показан пример обратной траектории, которая стартует в 12:00 по Гринвичу (17:00 по местному времени) 13 июня 2010 г. на высоте, соответствующей давлению 950 гПа. Показанная на рисунке 1.2 траектория характеризует путь воздушного потока на протяжении семи суток в точку расположения станции мониторинга сети AERONET на Среднем Урале (обозначена звездочкой).

Рисунок. 2.2 -. [Сергей3] Пример обратной траектории движения воздушного потока для точки мониторинга сети AERONET на Среднем Урале (13.06.2010, 12:00 UTC, 950 гПа)
Надежность информации о динамике атмосферы подтверждается множеством работ, посвященных оценкам точности модельных расчетов прямых и обратных траекторий движения воздушных частиц. Такие оценки выполняются на основе сравнения результатов моделирования с реальными траекториями, полученными в результате отслеживания передвижения специальных зондов [17,18] или же маркеров. В качестве маркеров могут выступать различные примеси, выпущенные в ходе поставленного эксперимента (инертные газы) или попадающие в атмосферу в результате явлений природного (пыльца, вулканический пепел) и техногенного характера (радиоактивные вещества), а также физические величины (потенциальная температура, удельная влажность, потенциальный вихрь), имеющие свойство сохраняться вдоль траекторий движения воздуха [9].
2.3 Методы статистики обратных траекторий
Совместный анализ обратных траекторий движения воздушных потоков и результатов измерений параметров атмосферы позволяет получать более обширную информацию о содержании атмосферных примесей, нежели описанные в первой главе методы. Например, методы статистики обратных траекторий позволяют на основе локальных измерений в одном или нескольких пунктах мониторинга и информации о динамике атмосферы восстанавливать пространственную структуру измеряемого параметра. Такая возможность основывается на двух положениях:
1) информация о поступлении примеси в атмосферу переносится к прибору из других пространственных областей благодаря движению воздушных потоков;
2) «пересечение» (прохождение над одной и той же территорией в разное время) траекторий движения воздушных частиц, несущих различные значения сигнала, позволяет локализовать области пространства с вероятно более высоким уровнем измеряемого признака.
Методы статистики обратных траекторий [3-5] были разработаны для решения задач оценки пространственной структуры полей измеряемой величины по данным локальных приборных измерений, выполненных в одной или нескольких фиксированных точках за большой период времени. Возможность оценки полей по данным измерений в отдельной точке реализуется за счет вовлечения в анализ информации о динамике атмосферных потоков.
Существующие методы СОТ условно можно разделить на три класса:
· методы Л. Эшбо – часто называемые методом расчета функции потенциального вклада источников [4];
· методы П. Зайберт – для расчета среднего поля концентраций [5];
· методы А. Штоля – для расчета распределенного среднего поля концентраций [6].
В любом из вариантов метода СОТ вся анализируемая территория разбивается неподвижной (эйлеровой) сеткой на множество фиксированных объемных ячеек. Важной составляющей всех методов СОТ является набор обратных траекторий. Расчет обратных траекторий начинается с момента выполнения измерения и производится с постоянным отрицательным шагом по времени. С каждой траекторией сопоставляется значение концентрации, характеризующей наличие примеси в атмосфере, измеренной в точке старта траектории. Переход от множества лагранжевых траекторий движения воздуха и связанных с ними результатов измерений к неподвижной эйлеровой расчетной сетке осуществляется с помощью различных статистических процедур усреднения и фильтрации (сглаживания) по тем точкам траекторий, которые находятся в соответствующей эйлеровой ячейке.
2.4 Общее описание метода флюид-локации атмосферы
В Институте промышленной экологии миру был представлен новый метод анализа полей концентраций примесей в атмосфере – метод флюид-локации атмосферы, являющийся развитием методов СОТ и впервые описанный в работах [10-12]. В методе ФЛА, как и в других аналогичных методах, в качестве исходных данных используются:
1) наборы траекторий движения воздушных частиц, которые представляют информацию о динамике атмосферы;
2) ряды приборных измерений в одной или нескольких точках мониторинга.
Метод флюид-локации атмосферы является модификацией метода Штоля. Разработка метода ФЛА проводилась с целью заменить интуитивные процедуры сглаживания и фильтрации итерационным решением уравнений переноса примеси в атмосфере.
В реализации метода ФЛА можно выделить три этапа.
Этап статистической оценки среднего поля концентрации. На этом этапе, как и в методе Штоля, проводится оценка среднего поля измеряемого признака (например, концентрации вещества) на основе метода Зайберт, но без использования логарифмирования и статистического сглаживания.
Для расчета среднего эффективного поля концентрации измеряемого признака в эйлеровой ячейке пространства используется усреднение по времени в виде:

(2.1)
где[Сергей4] Tij – общее время пребывания всех тр1екторий в ячейке i,j,;
φl – значение признака на траектории l в ячейке i,j,;
Δtl – время пребывания траектории l в ячейке i,j,; индексы i,j определяют эйлерову ячейку пространства,; индекс l - номер лагранжевой частицы (траектории движения),;
kl – номер точки k на траектории l внутри соответствующей эйлеровой ячеки i,j,;
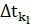 – шаг по времени на траектории l (в данной работе принят постоянным и равен 15 минут).
– шаг по времени на траектории l (в данной работе принят постоянным и равен 15 минут).
Интегрирование выполняется по времени нахождения траекторий внутри соответствующей эйлеровой ячейки, а суммирование – по всем лагранжевым частицам (траекториям движения) и всем точкам каждой траектории внутри эйлеровой ячейки. Очевидно, что в пределе бесконечно большого числа лагранжевых частиц и бесконечно малых размеров эйлеровых ячеек используемое в формуле (2.1) усреднение по времени теоретически совпадет с обычно применяемым в гидрогазодинамике определением средней величины. В случае конечных размеров эйлеровых ячеек и конечного числа траекторий лагранжевых частиц (из-за ограниченности числа выполненных измерений) величина среднего эффективного поля (2.1) представляет собой лишь статистическую оценку поля средней величины концентрации на основе конечного (возможно малого) числа ее значений в конкретные моменты времени.
Этап Эйлера. На основе среднего эффективного поля концентраций и поля скоростей движения воздуха оценивается поле мощностей источников/стоков, для чего используется уравнение сохранения, анализируемого (измеряемого прибором) признака φ в эйлеровом представлении:

| (2.2) |
где  – плотность потока признака
– плотность потока признака  ,;
,;
 – скорость движения воздуха,;
– скорость движения воздуха,;
 – мощность источников/стоков признака.
– мощность источников/стоков признака.
Запись уравнения (2.2) для ячейки конечного объема выглядит следующим образом:

| (2.3) |
где  – усреднение некоторой величины f по объему эйлеровой ячейки,;
– усреднение некоторой величины f по объему эйлеровой ячейки,;
S – площадь поверхности ячейки,;
 – элемент площади, ориентированный «наружу» ячейки.
– элемент площади, ориентированный «наружу» ячейки.
Уравнение (2.3) является точным уравнением сохранения, записанным в интегральной форме. Если поле признака φ известно, то уравнение можно использовать для вычисления мощностей источников и стоков, присутствующих в его правой части.
Считая среднее эффективное поле, найденное на первом этапе, оценкой пространственного распределения средней за период измерений концентрации, и используя (2.3), можно найти такое пространственное распределение поля источников, которое при известном поле скоростей ветра обеспечивает существование (согласно уравнению сохранения) этого исходного стационарного (усредненному по времени) поля концентраций.
Если считать, что в каждый момент времени прохождение воздушных частиц через соответствующую ячейку пространства соответствует «квазистационарному» состоянию (значение среднего по объему признака не меняется во времени – загрязнение остается в среднем неизменным), то уравнение (2.3) можно записать в разностной форме:

| (2.4) |
где  – усреднение некоторой величины
– усреднение некоторой величины  по временному интервалу
по временному интервалу  ,;
,;
 – текущее (k- е) значение времени внутри периода усреднения,;
– текущее (k- е) значение времени внутри периода усреднения,;
 ,;
,;
 – объем эйлеровой ячейки,;
– объем эйлеровой ячейки,;
 – значение среднего поля признака
– значение среднего поля признака  на границе
на границе 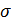 ,;
,;
 – значение проекции скорости ветра на внешнюю нормаль на границе
– значение проекции скорости ветра на внешнюю нормаль на границе  в момент времени
в момент времени  ,;
,;
 – площадь границы
– площадь границы  эйлеровой ячейки.
эйлеровой ячейки.
В зависимости от способа расчета значений признака 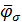 на границе эйлеровой ячейки можно получить различные разностные представления для расчета величины (2.4). Поскольку для нахождения
на границе эйлеровой ячейки можно получить различные разностные представления для расчета величины (2.4). Поскольку для нахождения  использовалось среднее поле
использовалось среднее поле  , то далее эта величина будет называться средним полем источников. Такое название подчеркивает, что при вычислении этой величины в формуле (2.4) использовались не истинные мгновенные значения концентраций, а усредненная (не изменяющаяся во времени) величина, являющаяся только оценкой этого поля – среднее поле концентраций.
, то далее эта величина будет называться средним полем источников. Такое название подчеркивает, что при вычислении этой величины в формуле (2.4) использовались не истинные мгновенные значения концентраций, а усредненная (не изменяющаяся во времени) величина, являющаяся только оценкой этого поля – среднее поле концентраций.
Этап Лагранжа. На основе найденной оценки поля мощностей источников/стоков рассчитывается распределение сигналов вдоль каждой траектории движения лагранжевой частицы с использованием уравнения сохранения в соответствующей форме. Дифференциальная запись уравнения сохранения признака в форме Лагранжа имеет вид:

| (2.5) |
Простейшая разностная форма для траектории с номером l записывается как:

| (2.6) |
Уравнение (2.6) позволяет пересчитать в обратном по времени направлении значение анализируемого признака вдоль каждой траектории, начиная с момента, когда значение признака было известно, т. е. с момента выполнения измерения. Таким образом, значение признака перераспределяется в пространстве вдоль траекторий движения лагранжевых частиц, так как в каждый момент времени координаты точек траектории рассчитаны.
После выполнения третьего этапа расчетов получим множество траекторий движения лагранжевых частиц, для которых значения переносимого ими признака уже не постоянно вдоль траекторий (как это неявно предполагается в различных вариантах методов СОТ). Это позволяет снова провести уточняющую процедуру статистической оценки среднего поля концентраций и затем повторить расчеты с использованием уравнений сохранения, выполняя итерации до тех пор, пока различия полей концентраций и источников, полученных на двух соседних итерациях, не будут меньше заданной погрешности итерационных вычислений. В результате на заданной реализации поля ветра будут получены физически согласованные поля (представления Эйлера и Лагранжа должны давать идентичное описание движения сплошной среды), являющиеся оценками поля концентраций и поля источников загрязнения.
Следует отметить, что каждый из трех этапов основного алгоритма разрабатываемого подхода представляет собой относительно независимую задачу, каждая из которых может быть решена различными методами. На первом этапе необходимо решить задачу статистической оценки параметра на основе выборки его значений конечного объема, что можно сделать разными способами, используя известные методы статистики (например, учитывая дополнительную информацию о виде функции распределения концентрации примеси, как это делается в оригинальном методе Зайберт [5]).
На втором этапе решается задача расчета поля источников по заданному полю концентрации примеси в движущейся среде. При решении этой задачи можно использовать различные способы усреднения по времени и разные способы определения поля скоростей ветра. Так, например, можно потребовать выполнение уравнения неразрывности за весь период анализа, т. е. на каждой итерации для каждой эйлеровой ячейки выполнять численное усреднение за несколько лет. При этом для нахождения скоростей движения воздуха необходимо либо выполнить за этот период времени прямое моделирование динамики атмосферы, либо использовать интерполяцию данных реанализа. В расчетах упрощенной демонстрационной задачи, решаемой ниже, использован другой подход: на этапе Эйлера предполагается выполнение закона сохранения массы только за ограниченный период времени – суммарное время прохождения всех учитываемых лагранжевых частиц (обратных траекторий) через рассматриваемую эйлерову ячейку, т. е. в формуле (2.4)  . Это позволило упростить расчеты путем использования известных значений скоростей движения воздуха на соответствующих обратных траекториях. При таком подходе формула (2.4) принимает вид:
. Это позволило упростить расчеты путем использования известных значений скоростей движения воздуха на соответствующих обратных траекториях. При таком подходе формула (2.4) принимает вид:
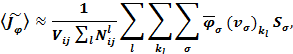
| (2.7) |
где  – объем эйлеровой ячейки,;
– объем эйлеровой ячейки,;
 – число точек траектории l внутри ячейки i,j,;
– число точек траектории l внутри ячейки i,j,;
l – номер траектории,;
 – значение проекции скорости лагранжевой частицы на внешнюю нормаль к границе
– значение проекции скорости лагранжевой частицы на внешнюю нормаль к границе 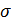 , соответствующее точке
, соответствующее точке  (т. е. в определенный момент времени).
(т. е. в определенный момент времени).
На третьем этапе решается задача определения изменения концентрации примеси вдоль траектории движения лагранжевой частицы в известном поле скоростей ветра и при известном распределении источников. В данной работе эта задача решается на множестве обратных траекторий движения воздушных частиц, начинающихся от места расположения прибора, т. е. от точки с известной (измеренной) концентрацией примеси.
Включение в предлагаемый метод этапа решения уравнений сохранения признака позволяет развивать предложенную методику в направлении учета реальных физико-химических процессов, происходящих с аэрозолем в атмосфере (гравитационное, сухое и влажное осаждения; физико-химические трансформации; турбулентная диффузия и др.). Таким образом, предлагаемый метод позволяет совместно использовать в расчетной схеме как результаты прямых приборных измерений, так и теоретические физико-химические модели рассматриваемого процесса переноса вещества в атмосфере.
Нужно заметить, что в тех задачах, где задаются или известны значения измеряемого признака на границах расчетной области, в полное множество анализируемых траекторий движения воздушных частиц можно включать не только обратные, но и прямые траектории. При этом обратные траектории должны начинаться с точки (точек), где располагается измерительный прибор, а прямые траектории должны рассчитыватьсярассчитываться, начиная с точек (областей) пространства, где заданы граничные условия (и/или мощности источников выбросов в атмосферу). Таким образом, разработанный метод допускает развитие в направлении его интеграции с традиционными методами моделирования при решении задач о распространении загрязняющих веществ в атмосфере.
2.5 Исходные данные для моделирования средних полей концентраций аэрозоля
Для демонстрации возможностей метода ФЛА в настоящей работе решалась упрощенная задача о нахождении поля концентрации атмосферного аэрозоля по данным фотометрических наблюдений в 2004–2010 гг. в шести пунктах аэрозольного мониторинга (AERONET) на территории России. В качестве признака, для которого решались уравнения сохранения, использовались объемные концентрации аэрозоля, восстановленные численным интегрированием из функции распределения аэрозольных частиц по размерам (рисунок 2.3). При расчете объемных концентраций выделялись две фракции: тонкодисперсная (частицы с радиусом r <0.76 мкм) и грубодисперсная (0.76 <r <15 мкм). Для моделирования полей аэрозольного наполнения атмосферы, формируемых дальним переносом (характерные размеры расчетной области – несколько тысяч километров), использовались значения концентраций только тонкодисперсной фракции аэрозоля. Стоит отметить, что функция распределения восстанавливается не для каждого измерения аэрозольной оптической толщи (АОТ). Для измерения величины АОТ достаточным условием является отсутствие заслоняющей облачности в области солнечного диска. При этом для решения задачи восстановления функции распределения аэрозольных частиц по размерам измеряются оптические характеристики атмосферы в альмукантарате солнца, т. е. весь небесный свод должен быть преимущественно свободен от облачности. Существуют также алгоритмы расчета микрофизических свойств аэрозоля на основе спектральной зависимости АОТ и априорного задания показателя преломления. [13,14]
Из всех станций AERONET, расположенных в России, были выбраны Звенигород, Москва, Екатеринбург, Томск, Якутск, Уссурийск, для которых:
1) есть продолжительные ряды наблюдений с 2004 по 2010 г.;
2) рассчитаны функции распределения аэрозоля по размерам;
3) выполняются расчеты обратных траекторий движения частиц.

Рисунок 2.3 -. Функции распределения аэрозольных частиц по размерам, восстановленные по результатам измерений в отдельные дни 2010 г.
Для учета имеющихся данных об обратных траекториях движения воздушных частиц и уменьшения объемов вычислений проводилось усреднение разовых измерений, и полученная среднедневная концентрация тонкодисперсного аэрозоля в дальнейшем использовалась при моделировании. Основные статистические характеристики полученных таким образом исходных данных, нормированные для удобства на медианное значение среднедневной концентрации тонкодисперсного аэрозоля в Екатеринбурге (0.025 мкм3/мкм2), приведены в табл.[Сергей5] ице 2.1.
Таблица 2.1 -. [Сергей6] Статистические характеристики рядов среднедневных концентраций тонкодисперсного аэрозоля по каждому пункту наблюдения
| Характеристика | Звенигород | Москва | Екатеринбург | Томск | Якутск | Уссурийск | Все станции |
| Число измерений | |||||||
| Минимум | 0.25 | 0.16 | 0.17 | 0.15 | 0.14 | 0.15 | 0.14 |
| 1 й квартиль | 0.67 | 0.67 | 0.60 | 0.60 | 0.45 | 0.68 | 0.60 |
| Медиана | 1.06 | 1.19 | 1.00 | 0.90 | 0.74 | 1.01 | 0.98 |
| Среднее | 1.55 | 1.51 | 1.20 | 1.20 | 0.97 | 1.52 | 1.32 |
| 3 й квартиль | 1.83 | 1.97 | 1.57 | 1.44 | 1.17 | 1.85 | 1.62 |
| Максимум | 11.72 | 14.07 | 5.21 | 13.46 | 7.65 | 12.80 | 14.07 |
Важной особенностью метода ФЛА является учет множества обратных траекторий движения воздушных частиц за период проведения измерений по каждому пункту мониторинга. Для обработки данных измерений сети AERONET использовались траектории, рассчитанные Т. Кучерой (GSFC/NASA) и представленные на сайте http://croc.gsfc.nasa.gov/aeronet. Использовались семисуточные обратные траекториина изобарической поверхности 950 гПа, что соответствует высоте около 500 м в пункте выполнения измерений.
Каждая траектория представляет собой набор точек, соответствующих положению лагранжевой частицы в пространстве в различные моменты времени, рассчитанные с шагом в 15 минут. В качестве иллюстрации множества используемых обратных траекторий и их протяженности в пространстве на рисунке 2.3 показаны траектории ограниченной длительности за 2010 г. на изобарической поверхности 950 гПа для шести пунктов мониторинга. Для сибирских и дальневосточных станций продолжительность траекторий, показанных на рисунке, составляет трое суток, а для европейских и уральской станций – двое суток. На рисунке 2.4 показаны обратные траектории только для пункта Уссурийск, но с длительностью семь дней.

Рисунок 2.4 -. Исходные данные – траектории движения лагранжевых частиц за 2010 г. на изобарической поверхности 950 гПа для каждой из шести станций мониторинга
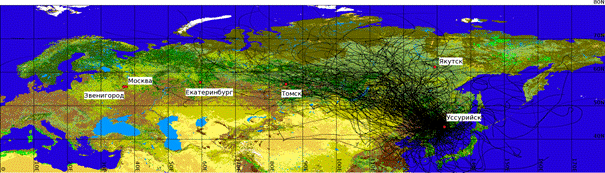
Рисунок 2.5 -. Исходные данные – семидневные траектории движения лагранжевых частиц за 2010 г. на изобарической поверхности 950 гПа для станции мониторинга Уссурийск
Использование в данной задаче лишь «нижних» траекторий на изобарической поверхности 950 гПа означает, что обсуждаемые далее результаты расчетов представляют квазидвумерные поля распределения концентрации тонкодисперсного аэрозоля в пространстве, т. е. являются лишь приближенной оценкой реальных трехмерных полей.
Численное решение задач восстановления пространственного распределения поля объемной концентрации тонкодисперсного аэрозоля по результатам измерений в российском сегменте сети AERONET проводилось внутри области от 0° до 150° в. д. и от 30° до 70° с. ш. Пространственное разрешение, соответствующее размерам ячеек эйлеровой сетки, для представляемых ниже результатов составило 1°×1°, хотя предварительно выполнялись методические расчеты с другими размерами ячеек. Большинство операций по графическому представлению данных и геоинформационному анализу выполнялось с использованием ГИС GRASS и QGIS [15]..
Date: 2016-07-18; view: 1370; Нарушение авторских прав