
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Экспериментальная часть
|
|
Введение
Обработка сигналов представляет собой практическую ценность, т.к. ищется оптимальная комбинация уровня потерь полезного сигнала к глубине подавления помех и их сумма (нелинейная задача), рассчитываются и сравниваются модели подавления по определенным критериям – это уже является повышением помехозащищенности и пропускной способности суммарного сигнала. Все это прямым образом влияет на стоимость всего оборудования в целом. Использование адаптивных систем, параметры которых автоматически меняются так, чтобы обеспечить наилучшее или приближающееся условия приема полезного сигнала на фоне изменяющихся мешающих внешних воздействий. С этой целью в данной работе рассматривается математическая модель адаптивных антенн, в которых принимаемые сигналы  мы элементами системы, проходят через устройства, регулирующие их амплитуду и фазу. Далее данные параметры складываются в сумматоре, каждый со своим весовым коэффициентом (ВК), обозначаемым
мы элементами системы, проходят через устройства, регулирующие их амплитуду и фазу. Далее данные параметры складываются в сумматоре, каждый со своим весовым коэффициентом (ВК), обозначаемым  . При отсутствии помехи (состояние покоя) ВК обеспечивают получение желаемой диаграммы направленности (ДН), а при наличии – подавление помехи. Процесс адаптации осуществляется путем обратного воздействия на устройства, управляющие ВК, которое обеспечивает подавление помех в соответствии с некоторым критерием, фиксирующим выполнение специфических требований, сопровождающих это подавление. Алгоритм называется аналоговым, если задача решается чисто схемным путем, цифровым, если он реализуется на ЭВМ, гибридным, когда ЭВМ после соответствующего расчета регулирует амплитуду и фазы сигналов.
. При отсутствии помехи (состояние покоя) ВК обеспечивают получение желаемой диаграммы направленности (ДН), а при наличии – подавление помехи. Процесс адаптации осуществляется путем обратного воздействия на устройства, управляющие ВК, которое обеспечивает подавление помех в соответствии с некоторым критерием, фиксирующим выполнение специфических требований, сопровождающих это подавление. Алгоритм называется аналоговым, если задача решается чисто схемным путем, цифровым, если он реализуется на ЭВМ, гибридным, когда ЭВМ после соответствующего расчета регулирует амплитуду и фазы сигналов.
В ряде расчетов могут возникнуть погрешности т.к. помехи не могут быть подавлены до абсолютного нуля. С учетом погрешностей, конечные результаты могут быть искаженными.
Итак, данная квалификационная работа Бакалавра состоит в создании алгоритма, который осуществляет подавление заданного количества помех с помощью изменения амплитуды и фазы сигнала. Так же, в данной работе, приведено решении дифференциального уравнения, которое описывает процесс адаптации весовых коэффициентов ВК при различной комбинации антенных решеток.
Был проведен численный эксперимент с помощью программных пакетов Matlab и Wolfram Mathematica. Часть численных расчетов проведена с использованием стандарта языка C++/11.
Таким образом, в данной работе приводится:
1. Создание оптимального алгоритма подавления помех;
2. Оценка эффективности алгоритма;
3. Анализ системы, моделирующей динамическое распределение помех во времени;
Адаптивная антенная решётка (ААР) — тип антенны, в которой динамическое изменение параметров и характеристик антенн меняется адаптивно к воздействиям внешних или внутренних факторов. Возможность адаптации повышает качество приёма сигнала. Отличие от обычных антенных систем заключено в изменении своих параметров под воздействием принимаемых сигналов
Адаптивные антенные системы или ААР применяются для передачи и приема радио сигнала широкого спектра диапазона (базис для работы операторов виртуальной связи, спутниковые системы связи, радиоастрономии, устройства гидролокации и пр.)
Цели и задачи – изучение работы адаптивных систем в антенных решетках и моделирование процесса адаптации мерцающих помех. В данной работе исследовано устройство адаптивной антенной решетки, применение ее на практике и систем для подавления мерцающих помех.
Актуальность работы – адаптивная обработка сигналов – это неиспользованный ресурс для создания пропускной способности и защищенности. В данной работе создан алгоритм для подавления помех при произвольной частоте, угле вхождения, в зависимости от времени. Разработана динамическая модель системы сигнал-шум.
Предметом исследования в данной работе является механизм адаптации помех.
Теоретическая и методологическая база исследования основана на открытых источниках литературы и научных статьях. Используется бесплатная графическая среда для построения диаграмм и схем Splan, матпакеты для численных расчетов, моделирования и визуализации данных Matlab, Wolfram Mathematica. Для проведения отдельных расчетов используется С++ в качестве программного средства.
Теоретическая значимость работы заключена в проектировании оптимального алгоритма подавления шумов, анализа эргодического уравнения случайного процесса: входной шум – выходное подавление шума, средний квадрат флуктуации процесса, получены диаграммы направленности (ДН) для случая одной и заданного количества помех.
Практическая значимость работы заключена в использовании приведенных алгоритмов для оборудования в устройстве антенных решеток и систем подавления. С одной стороны алгоритм является универсальным, так как скорость адаптации, в конечном счете, сводится к мощности ЭВМ. Но с другой, необходимо учитывать особенности применения той или иной ААР с приведенным алгоритмом на местности. В одних случаях необходимо маленькое значение времени настройки на помеху (суммарная обратная связь), и значения с несильно различным значением математического ожидания для того или иного момента времени, либо необходимо получить качественный сигнал игнорируя при этом длительность обратного отклика ААР.
Теоретическая часть
1.1Описание принципа работы адаптивных антенных систем
Разновидность антенны с обработкой сигналов, предназначенная для максимизации отношения сигнал/шум. Максимизация осуществляется автоматической регулировкой весовых коэффициентов, с которыми суммируются сигналы, поступающие от отдельных приемных каналов. Чаще всего адаптивной антенной является антенная решетка. Обычно обработка сигналов помех, обеспечивающая подавление суммарного сигнала помех на выходе адаптивной антенны, производится до приема полезного сигнала. Аппаратура системы обработки основана на использовании устройств для регулировки амплитуд и (или) фаз весовых коэффициентов. Регулировка весовых коэффициентов производится автоматически с помощью обратных связей между выходом системы обработки сигналов и приемными каналами адаптивной антенны. Глубина подавления помех, необходимый объем аппаратуры обработки сигналов зависят от используемого метода адаптации и его конкретной реализации. Полное подавление помехи до абсолютного нуля невозможно. Глубина подавления помехи зависит от уровня мощности  собственных шумов антенн, входящих в систему. Принято считать, что данные шума не коррелированны ни между собой, ни с помехой, ни с полезным сигналом [1]. Поэтому суммарная мощность собственных шумов системы из
собственных шумов антенн, входящих в систему. Принято считать, что данные шума не коррелированны ни между собой, ни с помехой, ни с полезным сигналом [1]. Поэтому суммарная мощность собственных шумов системы из  антенн:
антенн:
 (1)
(1)
Регулировка весовых коэффициентов ВК в процессе адаптации изменяет уровень собственных шумов, что необходимо учитывать при расчетах и при формулировке оценки подавления помех [2]. Данными критериями являются:
1. Максимум отношения  (ОСШП);
(ОСШП);
2. Минимум выходного суммарного шума при наличии неадаптируемых ВК у одной или нескольких антенн системы;
3. Минимум суммарного шума при защите от подавления полезного сигнала;
4. Наименьшее отклонение принимаемого сигнала от заданного образцового;
5. Оптимальное подавление помехи при условии стабильной мощности собственных шумов;
Объединение и оптимизация приведенных методов позволяет выбрать метод построения системы управления ВК. Рассмотрим основные положения теории.
1.2 Теоретическая модель адаптивных систем
К адаптивным системам относят системы (Рисунок 2), состоящие из  антенн и нескольких вспомогательных антенн. Используемых для защиты от помех, приходящих с направлений боковых лепестков ДН основной антенны. Основная антенна может быть как решетчатой так и зеркальной. Вспомогательные антенны – ненаправленные или слабонаправленные с ДН, обеспечивающей лучший прием помехи по сравнению с приемом полезного сигнала [3]. Число этих антенн должно быть равно максимальному числу источников помех, подлежащих подавлению. При учете собственных шумов адаптированная ДН системы
антенн и нескольких вспомогательных антенн. Используемых для защиты от помех, приходящих с направлений боковых лепестков ДН основной антенны. Основная антенна может быть как решетчатой так и зеркальной. Вспомогательные антенны – ненаправленные или слабонаправленные с ДН, обеспечивающей лучший прием помехи по сравнению с приемом полезного сигнала [3]. Число этих антенн должно быть равно максимальному числу источников помех, подлежащих подавлению. При учете собственных шумов адаптированная ДН системы  в направлении на помеху принимает значение:
в направлении на помеху принимает значение:

Где  – угол прихода помехи;
– угол прихода помехи;  и
и 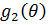 – значения ДН основной и добавочной антенн в направлении на помеху;
– значения ДН основной и добавочной антенн в направлении на помеху;  – отношение мощности помехи к мощности собственных шумов добавочной антенны (чем больше это отношение, тем глубже подавляется помеха). Минимальная мощность, вносимых добавочной антенной суммарных шумов
– отношение мощности помехи к мощности собственных шумов добавочной антенны (чем больше это отношение, тем глубже подавляется помеха). Минимальная мощность, вносимых добавочной антенной суммарных шумов  , которую обеспечивает рассматриваемый алгоритм адаптации:
, которую обеспечивает рассматриваемый алгоритм адаптации:

Она будет стремиться к нулю пропорциональной мощности  собственных шумов добавочной антенны при большой достаточной мощности помехи.
собственных шумов добавочной антенны при большой достаточной мощности помехи.

Рисунок 1. Распределение шума при средней мощности собственных шумов 

Рисунок 2. Принцип устройства Адаптивной Антенной Решетки
1.3 Адаптация по критерию максимума ОСШП
Пусть существует простейшая антенная система – линейная антенная решетка из  ненаправленных элементов, расположенных на расстоянии
ненаправленных элементов, расположенных на расстоянии  друг от друга. Ее ненормированная ДН
друг от друга. Ее ненормированная ДН  ) будет равна:
) будет равна:

А нормированная ДН:

Здесь  , а угол наблюдения
, а угол наблюдения  отсчитывается от нормали к оси решетки [4]. При ориентировке на прием с направления главного максимума ДН (
отсчитывается от нормали к оси решетки [4]. При ориентировке на прием с направления главного максимума ДН ( . Мощность собственных шумов при отсутствии помехи будет:
. Мощность собственных шумов при отсутствии помехи будет:

В то же время монохроматический сигнал, принимаемый решеткой и создающий мощность 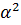 на входе канала, будет иметь на выходе мощность:
на входе канала, будет иметь на выходе мощность:

А отношение  (ОСШ) будет определяться как:
(ОСШ) будет определяться как:

Где  – мощность сигнала, принимаемого одним входным элементом. Выраженная через мощность его собственного шума. При наличии помехи ВК автоматически изменяются так, чтобы мощность суммарных шумов (собственных и остаточных от подавленной помехи) была минимальной. Методика [5] следующего расчета состоит в том чтобы при любом числе помех адаптированная ДН слагается из исходной диаграммы покоя, из которой вычитается ряд диаграмм равноамплитудной решетки, максимум из которых направлен на каждую из помех. Значение адаптированное ДН в направлении
– мощность сигнала, принимаемого одним входным элементом. Выраженная через мощность его собственного шума. При наличии помехи ВК автоматически изменяются так, чтобы мощность суммарных шумов (собственных и остаточных от подавленной помехи) была минимальной. Методика [5] следующего расчета состоит в том чтобы при любом числе помех адаптированная ДН слагается из исходной диаграммы покоя, из которой вычитается ряд диаграмм равноамплитудной решетки, максимум из которых направлен на каждую из помех. Значение адаптированное ДН в направлении  прихода одиночной помехи мощностью
прихода одиночной помехи мощностью  :
:

Где  исходная ДН покоя. Наибольшее ОСШП будет иметь место для равноамплитудной решетки – АР (с одинаковыми
исходная ДН покоя. Наибольшее ОСШП будет иметь место для равноамплитудной решетки – АР (с одинаковыми  . [6] При различных
. [6] При различных  оптимальное значение при этом ОСШП будет ниже наибольшего возможного. Остаточная мощность помехи после (при
оптимальное значение при этом ОСШП будет ниже наибольшего возможного. Остаточная мощность помехи после (при  :
:

Графически изобразим остаточную мощность помехи для случая (

Рисунок 3. Убывание мощности шума для случая N = 1
Обратно пропорционально своей величине. Для ОСШП описывается алгоритм независимо от мощности помехи:

Для подавления нескольких помех необходимо, чтобы их число не превышало  , (
, ( степеней свободы решетки). В отличие от других алгоритмов данный алгоритм обеспечивает сохранение исходной произвольной ДН при отсутствии помех. Однако он не обеспечивает защиты полезного сигнала. Чем мощнее помеха (Рисунок 4), тем быстрее и глубже она подавляется. Описываемый алгоритм применяется для защиты слабых и кратковременных сигналов, подобных радиолокационным. Переходя к адаптивным антеннам с критерием минимума выходных шумов, теоретически для этого требуется все ВК приравнять к нулю, что устраняет и прием полезного сигнала. [7] На практике, однако, однако, это требование устраняется путем введения некоторых ограничений или дополнительных условий, обеспечивающих выполнение того или иного другого критерия. Такими ограничениями в частности являются:
степеней свободы решетки). В отличие от других алгоритмов данный алгоритм обеспечивает сохранение исходной произвольной ДН при отсутствии помех. Однако он не обеспечивает защиты полезного сигнала. Чем мощнее помеха (Рисунок 4), тем быстрее и глубже она подавляется. Описываемый алгоритм применяется для защиты слабых и кратковременных сигналов, подобных радиолокационным. Переходя к адаптивным антеннам с критерием минимума выходных шумов, теоретически для этого требуется все ВК приравнять к нулю, что устраняет и прием полезного сигнала. [7] На практике, однако, однако, это требование устраняется путем введения некоторых ограничений или дополнительных условий, обеспечивающих выполнение того или иного другого критерия. Такими ограничениями в частности являются:
а) условие, что один выбранный заранее ВК в процесс адаптации не меняется;
б) условие фиксации мощности полезного сигнала, приходящего с заранее заданного направления;

Рисунок 4. Модель распространения двух помех на один лепесток ААР
Для потока входных сигналов (1) и (2), зависящих от времени:


Общая формула:

Основное уравнение, задающее связь между входных сигналом и настройкой весовых коэффициентов ВК:



Получено решение настройки ВК на помеху для N=4 числа компонент и одного шумового сигнала  . Компонент
. Компонент  помехи с углом у помехи
помехи с углом у помехи  , красный график эмулирует распределение помехи во времени, а синий ее подавление.
, красный график эмулирует распределение помехи во времени, а синий ее подавление.
1.4 Адаптация по критерию минимума шума
Обычно ограничение сводится к устранению подавления в направлении прихода полезного сигнала и фиксированного значения ненормированной ДН в этом направлении. При наличии одной помехи мощностью  значение адаптированной ДН эквидистантой решетки из
значение адаптированной ДН эквидистантой решетки из  элементов в направлении на помеху, будет:
элементов в направлении на помеху, будет:

 |
В направлении главного максимума (
 подавления не происходит. Если помеха приходит со стороны первого бокового лепестка, для которого
подавления не происходит. Если помеха приходит со стороны первого бокового лепестка, для которого  , то ее амплитуда подавляется почти в
, то ее амплитуда подавляется почти в  раз. [8] Даже если направление помехи задевает главный максимум и соответствует его половинной мощности, подавление в
раз. [8] Даже если направление помехи задевает главный максимум и соответствует его половинной мощности, подавление в  раз остается достаточно сильным.
раз остается достаточно сильным.
Рисунок 5. ДН для случая 
Теория адаптации по рассматриваемому критерию распространена и на случай нескольких помех. Данный алгоритм адаптации обеспечивается соответствующим подбором ВК и их регулировкой при изменении помеховой обстановки. Наиболее распространенным является гибридный алгоритм адаптации, при котором ЭВМ контролирует выходную мощность и посылает сигналы, управляющие величиной ВК. Рассматриваемый здесь способ адаптации не позволяет сохранять при отсутствии помехи ДН, отличную от ДН равноамплитудной решетки. Это связано с тем, что адаптирующая система, поддерживаемая неизменным значение ДН для защищаемого направления, автоматически переводит все ВК к одинаковому значению  , обеспечивая тем самым минимум мощности собственных шумов при отсутствии помехи. [9]
, обеспечивая тем самым минимум мощности собственных шумов при отсутствии помехи. [9]
Характерной особенностью рассматриваемого метода является сужение главного лепестка ДН, ориентированного на полезный сигнал. При подходе этого сигнала к максимуму со стороны боковых лепестков алгоритм адаптации подавляет его путем соответствующего подбора ВК до максимального значения ВК крайних облучателей решетки, равного:

Увеличение ВК (путем применения усилителей) вызывает возрастание мощности собственных шумов антенны, достигающей максимальной величины (при указанном значении  ), равной:
), равной:

В этот момент мощность полезного сигнала имеет ту же величину; дальше происходит только возрастание, а мощность шумов падает так, что ДН, снимаемая по ОСШП, становится очень узкой. Ее ширина по половинной мощности становится в  раз меньше по сравнению с ДН неадаптированной решетки. Адаптация по рассматриваемому принципу позволяет получить повышенную разрешающую способность, тем большую, чем больше мощность разрешающих сигналов. Эти результаты получаются после соответствующей обработки сигналов, принимаемых вибраторами решетки, и, следовательно, достигаются ценой потери некоторого времени. То есть время адаптации так же существенный критерий.
раз меньше по сравнению с ДН неадаптированной решетки. Адаптация по рассматриваемому принципу позволяет получить повышенную разрешающую способность, тем большую, чем больше мощность разрешающих сигналов. Эти результаты получаются после соответствующей обработки сигналов, принимаемых вибраторами решетки, и, следовательно, достигаются ценой потери некоторого времени. То есть время адаптации так же существенный критерий.
1.5 Адаптация к заданному количеству помех
Разновидность антенны с обработкой сигналов, предназначенная для максимизации отношения  .
.
Максимизация осуществляется автоматической регулировкой весовых коэффициентов, с которыми суммируются сигналы, поступающие от отдельных приемных каналов. Чаще всего адаптивной антенной является антенная решетка. Обработка сигналов поступающих помех, обеспечивающая подавление суммарного сигнала помех на выходе адаптивной антенны, производится до приема полезного сигнала, то есть вначале происходит настройка ВК на помеху или помехи. Аппаратура системы обработки основана на использовании устройств для регулировки амплитуд и (или) фаз весовых коэффициентов. Регулировка весовых коэффициентов производится автоматически с помощью обратных связей между выходом системы обработки сигналов и приемными каналами адаптивной антенны. Глубина подавления помех, необходимый объем аппаратуры обработки сигналов зависят от используемого метода адаптации и его конкретной реализации. Алгоритм и математическая модель описаны подробно в экспериментальной части.
1.6 Исследование математического аппарата для анализа работы ААР
В теории ААР в основном используется векторный и матричный математический аппарат для расчета исходных параметров принимаемых ААР детерминированных или случайных сигналов. Общая схема ААР изображена на Рисунке 6. Адаптивная антенная решетка представляет собой систему из  приемных и направленных элементов. Присоединяются фидерами одинаковой длины к сумматору
приемных и направленных элементов. Присоединяются фидерами одинаковой длины к сумматору  через устройство, изменяющее в
через устройство, изменяющее в  раз амплитуду и на
раз амплитуду и на  [рад],
[рад],  фазу принимаемого сигнала так, чтобы обеспечить на выходе сумматора подавление помехи в соответствии с одним из указанных в начале данной работы пяти критериев этого подавления. [10]
фазу принимаемого сигнала так, чтобы обеспечить на выходе сумматора подавление помехи в соответствии с одним из указанных в начале данной работы пяти критериев этого подавления. [10]
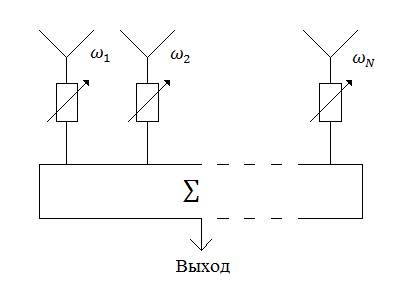
Рисунок 6. Общая схема ААР.
Простейшим случаем является, когда источник излучения достаточно удален и все элементы решетки обладают одинаковой направленностью и сигнал в свою очередь является узкополосным. Тогда амплитуды напряжений в каждом элементе приближенно одинаковые. И разница в расстояниях от источника до каждого из элементов будет проявляться лишь в соответствующем сдвиге фаз между ними. Поэтому сигнал, принятый  -м элементом, запишется в виде:
-м элементом, запишется в виде:



 зависящая от положения -го элемента и закона модуляции принимаемого сигнала, отсчитывается от фазы сигнала в каком-либо из каналов (стандартно – от фазы первого канала);
зависящая от положения -го элемента и закона модуляции принимаемого сигнала, отсчитывается от фазы сигнала в каком-либо из каналов (стандартно – от фазы первого канала);

 медленно меняющаяся амплитуда огибающей волны узкополосного сигнала, всегда различная для разных элементов.
медленно меняющаяся амплитуда огибающей волны узкополосного сигнала, всегда различная для разных элементов.
Радиосигналы с измененными амплитудами (во время  ) и фазами в каждом канале:
) и фазами в каждом канале:

Складываясь в сумматоре, формируют выходной сигнал ААР:

Для комплексного представления радиосигнала (17) в -м канале является по определению комплексная функция:

А комплексная амплитуда получается из (20) отбрасыванием временной зависимости в показателе степени экспоненты:

Используя комплексное представление радиосигналов, запишем комплексную амплитуду сигнала на выходе ААР:

Таким образом, ААР осуществляет взвешенное суммирование радиосигналов, принятых своими элементами. Физическая реализация взвешивания, в смысле умножения на комплексные ВК комплексных амплитуд радиосигналов, осуществляется с помощью управляемых аттенюаторов и фазовращателей или с помощью управляемых усилителей. [11]
Другой способ изменения амплитуды и фазы радиосигнала основан на изменении усиления амплитуд, так называемых синфазной  и квадратурной
и квадратурной  компонент радиосигнала
компонент радиосигнала  , определяемых в соответствии с равенствами:
, определяемых в соответствии с равенствами:


Для определения закона изменения усиления синфазной и квадратурной компонент радиосигнала, эквивалентного изменению амплитуды и фазы реального радиосигнала, представим (18) в виде суммы синфазной и квадратурной компонент:

 (25)
(25)
Где требующие усиления синфазной и квадратурной компонент обозначены соответственно:
 (26)
(26)
 (27)
(27)
И соответствуют (23) и (24). Далее везде будут рассматриваться в основном комплексные представления. Индекс  в обозначении комплексных амплитуд опустим. В ААР комплексные ВК
в обозначении комплексных амплитуд опустим. В ААР комплексные ВК  в каждом канале устанавливаются автоматически в зависимости от вида входных сигналов и цели, которую преследует адаптивное управление. Устройства формирования ВК могут иметь различные принципы функционирования (аналоговый, цифровой, гибридный). Подбор ВК
в каждом канале устанавливаются автоматически в зависимости от вида входных сигналов и цели, которую преследует адаптивное управление. Устройства формирования ВК могут иметь различные принципы функционирования (аналоговый, цифровой, гибридный). Подбор ВК  при суммировании сигналов с выходов линий задержки определяет частотную характеристику системы. Следовательно, при адаптивном управлении этими весами возможно изменение частотной характеристики антенн, с целью максимального ослабления действующей на антенну помехи определенной частоты. Для реального случая, когда ААР обрабатывает совокупность сигналов
при суммировании сигналов с выходов линий задержки определяет частотную характеристику системы. Следовательно, при адаптивном управлении этими весами возможно изменение частотной характеристики антенн, с целью максимального ослабления действующей на антенну помехи определенной частоты. Для реального случая, когда ААР обрабатывает совокупность сигналов  , принятых в разных точках пространства с помощью целенаправленного изменения ВК
, принятых в разных точках пространства с помощью целенаправленного изменения ВК  используется векторно-матричный аппарат. Для ААР совокупность принятых сигналов
используется векторно-матричный аппарат. Для ААР совокупность принятых сигналов  можно записать в виде с помощью вектора столбца
можно записать в виде с помощью вектора столбца  :
:
 (28)
(28)
Этот же вектор иногда удобно использовать в транспонированном виде:
 (29)
(29)
Для комплексного представления:
 (30)
(30)
Рассмотрим вектор  сигналов, принятых произвольной решеткой, составленной из
сигналов, принятых произвольной решеткой, составленной из  направленных приемных элементов, ненормированные ДН которых (отнесенные к их выводу) задаются комплексными функциями
направленных приемных элементов, ненормированные ДН которых (отнесенные к их выводу) задаются комплексными функциями  , где
, где  наблюдения, отсчитываемый от некоторого, наперед заданного направления. Ненормированные ДН приемного элемента определяем как отклик приемного элемента на сигнал единичной амплитуды, источник которого перемещается относительно антенны. Фаза
наблюдения, отсчитываемый от некоторого, наперед заданного направления. Ненормированные ДН приемного элемента определяем как отклик приемного элемента на сигнал единичной амплитуды, источник которого перемещается относительно антенны. Фаза  измеряется в точке выхода антенны и отсчитывается по отношению к фазе сигнала, принимаемого с выбранного заранее направления. Тогда:
измеряется в точке выхода антенны и отсчитывается по отношению к фазе сигнала, принимаемого с выбранного заранее направления. Тогда:
 (31)
(31)
Где 
 среднеквадратичное напряжение радиосигнала, принимаемого ненаправленным элементом. А
среднеквадратичное напряжение радиосигнала, принимаемого ненаправленным элементом. А  определяет фазу огибающей сигнала на входе
определяет фазу огибающей сигнала на входе  го приемного элемента за счет пространственного разнесения элементов ААР.
го приемного элемента за счет пространственного разнесения элементов ААР.  = 0, т.к. фаза условно отсчитывается по отношению к фазе сигнала на выходе первого элемента решетки.
= 0, т.к. фаза условно отсчитывается по отношению к фазе сигнала на выходе первого элемента решетки.
При приеме нескольких радиосигналов, источники которых находятся в дальней зоне, в направлениях, задаваемых углами  :
:
 (32)
(32)
Где 
 среднеквадратичное напряжение
среднеквадратичное напряжение  - го источника радиосигнала:
- го источника радиосигнала:
 (33)
(33)
Где  - фаза
- фаза  - ого радиосигнала на выходе
- ого радиосигнала на выходе  - ого приемного канала, отсчитываемая в соответствии с оговоренным ранее условием. В данной работе рассматривается линейная эквидистантная ААР с
- ого приемного канала, отсчитываемая в соответствии с оговоренным ранее условием. В данной работе рассматривается линейная эквидистантная ААР с  ненаправленными элементами, принимающий сигнал от источника в дальней зоне в направлении
ненаправленными элементами, принимающий сигнал от источника в дальней зоне в направлении  относительно нормали решетки:
относительно нормали решетки:
 (34)
(34)
Где 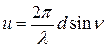 ;
; 
 длина волны;
длина волны; 
 межэлементное расстояние.
межэлементное расстояние.
Компактное представление выходных сигналов ААР в виде скалярного умножения:
 (35)
(35)
Данное выражение используются также и для расчета ненормированных диаграмм направленности ААР, т.к. по определению ДН – отклик антенны как функции угла прихода  или
или  сигнала от источника в дальней зоне при его различном положении относительно антенны. [12] Ненормированная диаграмма направленности ААР в масштабе весовых коэффициентов
сигнала от источника в дальней зоне при его различном положении относительно антенны. [12] Ненормированная диаграмма направленности ААР в масштабе весовых коэффициентов  равна:
равна:
 (36)
(36)
Рассмотрим симметричную эквидистантную синфазную решетку из четного числа  вибраторов с вещественными весовыми коэффициентами:
вибраторов с вещественными весовыми коэффициентами:
 (37)
(37)
Данные ВК формируют некоторую симметричную ДН, ненормированное значение которой в защищаемом главном направлении будет:
 (38)
(38)
Условие ограничения запишем в виде:
 (39)
(39)
Где  вектор принимаемого сигнала:
вектор принимаемого сигнала:
 (40)
(40)
Данное условие задает только амплитуду для  . В процессе адаптации указанные ВК изменяются как по амплитуде, так и по фазе. Их умножение на соответствующее комплексное число эквивалентно включению последовательно с исходными
. В процессе адаптации указанные ВК изменяются как по амплитуде, так и по фазе. Их умножение на соответствующее комплексное число эквивалентно включению последовательно с исходными  некоторых регулируемых
некоторых регулируемых  , что для установившихся оптимальных ВК дает значение
, что для установившихся оптимальных ВК дает значение  . Логично предположить, что до начала процесса адаптации
. Логично предположить, что до начала процесса адаптации  =1.
=1.
Экспериментальная часть
2.1 Результаты моделирования настройки ВК на помеху
Получен результат работы алгоритма для настройки ВК на помеху для выбранного числа компонент  и одного шумового сигнала
и одного шумового сигнала  . Компонента
. Компонента  определяет подавление
определяет подавление  помехи. Для эмуляции процесса адаптации был выбран угол
помехи. Для эмуляции процесса адаптации был выбран угол  .
.

Рисунок 5. Красный график – распределение ВК во времени. Синий – подавление.
2.2 Результаты моделирования для разных значений угла
Результаты расчетов основаны на расчете функции:
 (41)
(41)
Матрица входных сигналов:
 (42)
(42)
В общем виде:
 (43)
(43)
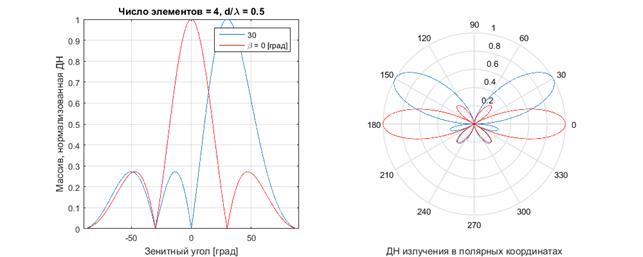
Рисунок 6. Нормированная ДН для 

Рисунок 7. Диаграмма излучения при угле помехи 

Рисунок 8. Нормированная ДН при угле помехи 

Рисунок 9. Диаграмма излучения при угле помехи 

Рисунок 10. Нормированная ДН при угле помехи 

Рисунок 11. Диаграмма излучения при угле помехи 
Проведем численные расчеты глубины подавления помехи для разных углов вхождения помехи и для количества элементов 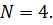
 , град , град
| 
| 
|
| 17.054 | 10.648 | |
| 17.054 | 13.324 | |
| 17.054 | 14.640 | |
| 17.054 | 14.523 | |
| 17.054 | 14.549 | |
| 17.054 | 13.538 | |
| 17.054 | 13.616 | |
| 17.054 | 12.690 | |
| 17.054 | 12.546 | |
| 17.054 | 9.692 | |
| 17.054 | 11.263 |
Таблица 1. Результаты численного эксперимента
Среднее значение глубины подавления:
 (44)
(44)
Абсолютная погрешность:
 (45)
(45)
Среднеквадратичное отколнение:
 (46)
(46)

Рисунок 12. Зависимость угла от глубины подавления мерцающей помехи.
2.4 Дополнительные шумы адаптивных антенн
Подавление помехи в адаптивной антенне сопровождается наличием шумов, зависящих от собственных шумов элементов антенны и от величины весовых коэффициентов. Помимо шумов, связанных с внутренними характеристиками рассматриваемой системы существуют и другие шумы:
1. Из-за флуктуаций в цепях управления;
2. Из-за квантовая ВК;
3. Из-за квантования сигналов при цифровом алгоритме адаптации;
Отношение мощности дополнительных шумов к мощности всех шумов называется рассогласованием и характеризует как зашумленность полезного сигнала на выходе адаптивных антенных решеток, так и реальную глубину подавления помехи. Теория показывает, что шумы из-за флуктуаций в цепях управления проявляются тем сильнее, чем больше коэффициент усиления в цепях обратной связи, а также чем шире частотная полоса шумов. По этой причине существуют максимально допустимое быстродействие цепей адаптации.
Шумы квантования ВК проявляются в виде увеличения уровня собственных шумов на величину, обратно пропорциональную мощности принимаемого сигнала к квадрату дискретного момента квантования. Возможно выбрать такой дискретный момент квантования ВК, при котором происходит увеличение шумов и амплитуд не более чем до заданного уровня.
Аналогичным образом сказываются шумы из-за квантовая принимаемых сигналов при цифровом алгоритме адаптации.
Заключение
В данной работе проведено изучение работы ААР на базе основных элементов цепи и надстройки ВК на помеху. Разработан специальный алгоритм адаптации в среде Matlab. Получена целостная математическая модель с учетом наличия заданного количества помех и количества элементов решетки. Построены ДН для нескольких случаев. Даже с учетом наличия внутренних и внешних шумов в системе ААР можно добиться оптимального значения величины ОСШП. Сглаживание внутренних и внешних шумов возможно при дополнении системы нейронной сетью, которая нацелена на уменьшение ошибки (то есть внешнего либо внутреннего шума для ААР).
Список литературы
1. Стратанович. Принципы адаптивного приема, М.: Сов Радио,1973,144с.
2. Литвинов О.С. Аналитические свойства ковариационной матрицы помех // Антенны. М.; Связь, 1982. С. 65-78. Вып. 30.
3. Абрамович Ю. И., Неврев А. И. Анализ эффективности адаптивной максимизации отношения сигнал\помеха, использующий образуемые оценки корреляционной матрицы// РЭ. Т.26,№12.С.2558-2566.
4. Аоки М. Введение в методы оптимизации функционалов. М.; Наука, 1976. 344с
5. Ширман Я. Д., Манжос В.Н. Теория и техника обработки информации на фоне помех. М.; Радио и связь, 1981, 416с.
6. Аоки М. Введение в методы стохастического программирования. М.; Наука, 1972. 424с.
7. Монцинго Р. А., Миллер Т.У. Адаптивные антенные решётки/ Пер.с англ, М..; Мир, 1986. 448с.
8. Стренг Г. Линейная алгебра и её применение. М.; Мир, Сов. Радио, 1975. 304 с
9. Ланкастер П. Теория матриц. М.: Наука, 1978, 280с.
10. [Электронный ресурс] // Жанкевич А. О. Математическая модель адаптивного устройства приема радиосигналов в условиях сложной радиоэлектронной обстановки
http://cyberleninka.ru/article/n/matematicheskaya-model-adaptivnogo-ustroystva-priema-radiosignalov-v-usloviyah-slozhnoy-radioelektronnoy-obstanovki
11. [Электронный ресурс] Aerospace engineering, orbital mechanics, space environment, weather and more matlab teaching codes
https://smallsats.org/tag/mst-radars/
12. [Электронный ресурс] The U.S. Department of Energy Office of Science is the lead federal agency supporting fundamental scientific research for energy and the Nation’s largest supporter of basic research in the physical sciences
http://science.energy.gov/news/highlights/
Приложение 1
Код настройки ВК:
gamma = input('Введите значение \gamma: ');
b = input('Введите значение \tau: ');
N = input('Введите количество компонент N: ');
theta = input('Введите начальное значение угла \theta: ');
delta = input('Введите шаг (например 0.01): ');
w = input('Введите значение \omega: ');
f=@(t,w)(theta.*((exp(t-N.*cos(t*w))/gamma.*(b+1)))); %ДУ для N количества компонент
[t,w]=ode45(f,1:delta:10,1);
plot(20log10(abs(w)/w),t,'r-','LineWidth',2)
hold on
title('Настройка ВК на помеху \theta');
plot(w,1./t,'b','LineWidth',2)
grid on
ylabel('g(\theta,t)')
xlabel('t')
legend('Arg|w|','g(\theta,t)')
Код адаптации к внешней помехе:
N = input('Введите количество элементов N: ');
d_l = 0.5;
alfa0 = input('Введите значение \omega: ');
alfa = -180:0.1:180; % Zenith angle
Ed = (abs(sin(pi*d_l*N*(sind(alfa) - sind(alfa0)))./...
sin(pi*d_l*(sind(alfa) - sind(alfa0))))/N);
Ed0 = (abs(sin(pi*d_l*N*(sind(alfa)))./...
sin(pi*d_l*sind(alfa)))/N);
g = 20*log10(Ed);
g0= 20*log10(Ed0);
fig = figure(1);
set(fig,'Position', [100, 100, 1000, 400]);
subplot(2,2,[1 3]);
plot(alfa,Ed);
hold on;
plot(alfa,Ed0,'r');
grid on;
axis([-90 90 0 1]);
xlabel('Зенитный угол [град]');
ylabel('Массив, нормализованная ДН');
title(['Число элементов = ',num2str(N),', d/\lambda = 0.5']);
legend(num2str(alfa0),'\beta = 0 [град]','Положение','3')
subplot(2,2,[2 4]);
polar(alfa*pi/180,Ed);
hold on;
polar(alfa*pi/180,Ed0,'r');
hold on;
xlabel('ДН излучения в полярных координатах');
hold off;
figure(2);
plot(alfa,g);
hold on;
plot(alfa,g0,'r');
grid on;
legend(num2str(alfa0),'\beta = 0 [град]','Положение','3')
axis([-90 90 -100 0]);
xlabel('Зенитный угол [град]');
ylabel('Диаграмма излучения дБ');
title(['Число элементов = ',num2str(N),', d/\lambda = 0.5']);
Код для вычисления средних значений на С++:
#include "stdafx.h"
#include "math.h"
#include <iostream>
#include "conio.h"
#define pi 3.141592653589793238
using namespace std;
int N;
double alfa0;
void mean_of_func_g_theta()
{
double sum1 = 0, sum2 = 0, d_l = 0.5, mean1 = 0, mean2 = 0;
for(int i = -180; i < 180; i ++)
{
sum1 = sum1 + abs(sin(pi*d_l*N*(sin(i*pi/180)-sin(alfa0))));
sum2 = sum2 + abs(sin(pi*d_l*(sin(i*pi/180)-sin(alfa0*pi/180))))/N;
}
mean1 = sum1/180;
mean2 = sum2/180;
double s = mean1/mean2;
s=log10(s);
cout <<"\n1: " << mean1 << endl;
cout <<"\n2: " << mean2 << endl;
cout <<"\nСреднее значение " << s << endl;
}
void mean_of_func_g_theta_null()
{
double sum1 = 0, sum2 = 0, d_l = 0.5, mean1 = 0, mean2 = 0;
for(int i = -180; i < 180; i ++)
{
sum1 = sum1 + abs(sin(pi*d_l*N*(sin(i*pi/180))));
sum2 = sum2 + sin(pi*d_l*sin(i*pi/180))/N;
}
mean1 = sum1/180;
mean2 = sum2/180;
double s = mean1/mean2;
s=log10(s);
cout <<"\n1: " << mean1 << endl;
cout <<"\n2: " << mean2 << endl;
cout <<"\nСреднее значение " << s << endl;
}
int _tmain(int argc, _TCHAR* argv[])
{
setlocale(LC_ALL,"rus");
cout <<"\nВведите количество элементов: ";
cin >> N;
cout <<"\nВведите угол вхождения: ";
cin >> alfa0;
mean_of_func_g_theta();
mean_of_func_g_theta_null();
_getch();
return 0;
}
| <== предыдущая | | | следующая ==> |
| | | Глава № 1 - Северная духовная академия |
Date: 2016-07-18; view: 515; Нарушение авторских прав