
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Примеры решения задач
|
|
По математике
Заочная форма обучения Преподаватель: к. п. н., доцент Макусева Т.Г.
Теоретическое задание для студентов, пропустивших установочную сессию (начитку).
Ответьте письменно на вопросы.
1. Сформулировать правило произведения.
2. Указать формулы для подсчета числа размещений при выборке с повторениями и без повторений.
3. Записать формулы для подсчета числа сочетаний.
4. Понятие случайного, достоверного и невозможного событий.
5. Вероятность суммы и произведения событий.
6. Классическое и геометрическое определение вероятности.
7. Повторные независимые испытания. В каких случаях применяются формулы Бернулли, Пуассона, локальная и интегральная формулы Муавра –Лапласа?
Решить задачи.
1. В урне содержится К черных и Н белых шаров. Случайным образом вынимаем М шаров. Найти вероятность того, что среди них имеется: а) Р белых шаров; в) меньше, чем Р, белых шаров; с) хотя бы один белый шар. Значения параметров К, Н, М и Р по вариантам:
| Вариант | ||||||||||||||||||||||||||||||
| К | ||||||||||||||||||||||||||||||
| Н | ||||||||||||||||||||||||||||||
| М | ||||||||||||||||||||||||||||||
| Р | ||||||||||||||||||||||||||||||
| Вариант | ||||||||||||||||||||||||||||||
| К | ||||||||||||||||||||||||||||||
| Н | ||||||||||||||||||||||||||||||
| М | ||||||||||||||||||||||||||||||
| Р | ||||||||||||||||||||||||||||||
2. Устройство состоит из трех независимых элементов, работающих в течении времени Т безотказно с вероятностями р  ,р
,р  ,р
,р  . Найти вероятность того, что за время Т выйдет из строя: а) только один элемент; б) хотя бы один элемент. Значения параметров вычислить по следующим формулам: k =
. Найти вероятность того, что за время Т выйдет из строя: а) только один элемент; б) хотя бы один элемент. Значения параметров вычислить по следующим формулам: k = 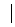 14,9 – V
14,9 – V 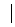 : 100; р
: 100; р  = 1– k, р
= 1– k, р  = 0,9 – k,
= 0,9 – k,
р  = 0,85 – k, где V– номер варианта.
= 0,85 – k, где V– номер варианта.
3. В пирамиде стоят R винтовок, из них L с оптическим прицелом. Стрелок, стреляя из винтовки с оптическим прицелом, может поразить мишень с вероятностью р  , а стреляя из винтовки без оптического прицела, – с вероятностью р
, а стреляя из винтовки без оптического прицела, – с вероятностью р  . Найти вероятность того, что стрелок поразит мишень, стреляя из случайно взятой винтовки. Значения параметров:
. Найти вероятность того, что стрелок поразит мишень, стреляя из случайно взятой винтовки. Значения параметров:
k = 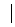 14 – V
14 – V 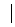 , где V– номер варианта, р
, где V– номер варианта, р  = 0,95 – k: 100, р
= 0,95 – k: 100, р  = 0,6 – k: 100,
= 0,6 – k: 100,
R = 5 + k, L = 3, если V  14; L = 4, если V>14.
14; L = 4, если V>14.
4. В урне содержится К белых и L черных шаров, а в другой М белых и Nчерных шаров. Из первой урны случайным образом вынимают P шаров и опускают во вторую урну. После этого из второй урны также случайно вынимают R шаров. Найти вероятность того, что все шары, вынутые из второй урны, белые.
| Вариант | |||||||||||||||||||||||||||||||
| К | |||||||||||||||||||||||||||||||
| L | |||||||||||||||||||||||||||||||
| M | |||||||||||||||||||||||||||||||
| N | |||||||||||||||||||||||||||||||
| P | |||||||||||||||||||||||||||||||
| R | |||||||||||||||||||||||||||||||
| Вариант | |||||||||||||||||||||||||||||||
| К | |||||||||||||||||||||||||||||||
| L | |||||||||||||||||||||||||||||||
| M | |||||||||||||||||||||||||||||||
| N | |||||||||||||||||||||||||||||||
| P | |||||||||||||||||||||||||||||||
| R | |||||||||||||||||||||||||||||||
5.
1.В некоторой местности в сентябре в среднем бывает 12 дождливых дней. Какова вероятность, что из случайно взятых в этом месяце восьми дней три дня окажутся дождливыми?
2. Два равносильных шахматиста играют в шахматы. Что вероятнее: выиграть две партии из четырех или три партии из шести (ничьи во внимание не принимаются).
3. Что вероятнее, выиграть у равносильного противника (ничейный исход партии исключен) три партии из четырех или пять из восьми?
4. Монету бросают пять раз. Найти вероятность того, что «герб» выпадет: а) менее двух раз, б) не менее двух раз.
5. Вероятность рождения мальчика равна 0,515, девочки 0,485. В некоторой семье шестеро детей. Найти вероятность, что среди них не больше 2-х девочек.
6. Изделия некоторого производства содержат 5% брака. Найти вероятность того, что среди пяти, взятых наугад, изделий: а) нет ни одного испорченного; б) будут два испорченных.
7. Всхожесть семян данного сорта растений оценивается с вероятностью, равной 0,8. Какова вероятность того, что из пяти посеянных семян взойдут не менее четырех?
8. В семье пятеро детей. Найти вероятность того, что среди этих детей: а) два мальчика; б) не более двух мальчиков. Вероятность рождения мальчика принять, равной 0,51.
9. Вероятность получения удачного результата при производстве сложного химического опыта равна 2/3. Найти наивероятнейшее число удачных опытов, если общее их количество равно 7.
10. Вероятность попадания в цель при каждом выстреле из орудия равна 0,8. Сколько нужно произвести выстрелов, чтобы наивероятнейшее число попаданий было равно 20?
11. Вероятность попадания в цель при каждом выстреле равна 0,001. Найти вероятность попадания в цель двух пуль и более, если число выстрелов равно 5000.
12. Вероятность того, что любой абонент позвонит на станцию в течение часа, равна 0,01. Телефонная станция обслуживает 800 абонентов. Какова вероятность, что в течение часа позвонят 5 абонентов.
13. Имеется общество из 500 человек. Найти вероятность того, что у двух человек день рождения придется на Новый год. Считать, что вероятность рождения в фиксированный день
равна 1/365.
14. Учебник издан тиражом 100000 экземпляров. Вероятность того, что учебник сброшюрован неправильно, равна 0,0001. Найти вероятность того, что тираж содержит ровно пять бракованных книг.
15. Завод отправил на базу 500 изделий. Вероятность повреждения изделия в пути равна 0,002. Найти вероятность того, что в пути будет повреждено изделий: а) более трех; г) хотя бы одно.
16. Магазин получил 1000 бутылок минеральной воды. Вероятность того, что при перевозке бутылка окажется разбитой, равна 0,003. Найти вероятность того, что магазин получит разбитых бутылок: a) ровно две, б)хотя бы одну (принять e-3=0,04979).
17. Вероятность появления успеха в каждом испытании равна 0,25. Какова вероятность, что при 300 испытаниях успех наступит: а) ровно 75 раз, б) ровно 85 раз?
18. В первые классы должно быть принято 200 детей. Определить вероятность того, что среди них окажется 100 девочек, если вероятность рождения мальчика 0,515.
19.Найти вероятность того, что событие А наступит ровно 70 раз в 243 испытаниях, если вероятность появления этого события в каждом испытании равна 0,25.
20. Вероятность появления события А в каждом из 100 независимых испытаний постоянна и равна р = 0,8. Найти вероятность того, что событие появится: а) не менее 75 раз
и не более 90 раз; б) не более 74 раз.
6. Закон распределения дискретной случайной величины представлен в таблице. Необходимо:
1) проверить, является ли данная таблица законом распределения дискретной случайной величины;
2) определить математическое ожидание M(X), дисперсию D(X) и среднеквадратичное отклонение s(x);
3) построить график этого закона распределения вероятностей.
Вариант №1.
| X | |||||||
| pi | 0,01 | 0,12 | 0,23 | 0,28 | 0,19 | 0,11 | 0,06 |
Вариант №2
| X | |||||||
| pi | 0,20 | 0,31 | 0,24 | 0,13 | 0,07 | 0,04 | 0,01 |
Вариант №3
| X | |||||||
| pi | 0,04 | 0,08 | 0,32 | 0,31 | 0,15 | 0,08 | 0,02 |
Вариант №4
| X | |||||||
| pi | 0,42 | 0,23 | 0,15 | 0,10 | 0,06 | 0,03 | 0,01 |
Вариант №5
| X | |||||||
| pi | 0,03 | 0,29 | 0,12 | 0,15 | 0,21 | 0,16 | 0,04 |
Вариант №6
| X | |||||||
| pi | 0,05 | 0,12 | 0,18 | 0,30 | 0,18 | 0,12 | 0,05 |
Вариант №7
| X | |||||||
| pi | 0,06 | 0,08 | 0,12 | 0,24 | 0,33 | 0,14 | 0,03 |
Вариант №8
| X | |||||||
| pi | 0,16 | 0,25 | 0,25 | 0,16 | 0,10 | 0,05 | 0,03 |
Вариант №9
| X | |||||||
| pi | 0,02 | 0,38 | 0,30 | 0,16 | 0,08 | 0,04 | 0,02 |
Вариант №10
| X | |||||||
| pi | 0,08 | 0,10 | 0,14 | 0,17 | 0,19 | 0,18 | 0,14 |
Вариант №11
| X | |||||||
| pi | 0,03 | 0,10 | 0,24 | 0,27 | 0,18 | 0,12 | 0,06 |
Вариант №12
| X | |||||||
| pi | 0,01 | 0,05 | 0,08 | 0,11 | 0,25 | 0,30 | 0,20 |
Вариант №13
| X | |||||||
| pi | 0,05 | 0,10 | 0,20 | 0,30 | 0,18 | 0,12 | 0,05 |
Вариант №14
| X | |||||||
| pi | 0,07 | 0,10 | 0,20 | 0,27 | 0,23 | 0,12 | 0,01 |
Вариант №15
| X | |||||||
| pi | 0,04 | 0,13 | 0,22 | 0,25 | 0,18 | 0,10 | 0,08 |
Вариант №16
| X | |||||||
| pi | 0,02 | 0,17 | 0,21 | 0,26 | 0,18 | 0,11 | 0,05 |
Вариант №17
| X | |||||||
| pi | 0,05 | 0,10 | 0,20 | 0,30 | 0,18 | 0,12 | 0,05 |
Вариант №18
| X | |||||||
| pi | 0,07 | 0,10 | 0,20 | 0,27 | 0,23 | 0,12 | 0,01 |
Вариант №19
| X | |||||||
| pi | 0,04 | 0,15 | 0,21 | 0,30 | 0,20 | 0,08 | 0,02 |
Вариант №20
| X | |||||||
| pi | 0,03 | 0,08 | 0,29 | 0,35 | 0,15 | 0,07 | 0,03 |
Примеры решения задач
Пример 1
Студент знает 15 вопросов из 30 в первом разделе курса и 25 из 40 вопросов второго раздела этого курса. В билете по одному вопросу из каждого раздела. Найти вероятность того, что студент:
1) знает ответы на оба вопроса;
2) не знает ответов на оба вопроса;
3) знает ответ только на один вопрос в билете.
n1 = 30, т1 = 15, n2 =40, m2 =25.
Решение
Обозначим общее число вопросов первого раздела курса n1 =30, а количество выученных вопросов этого раздела (т.е. благоприятствующих хорошему ответу) т1 = 15.
Общее число вопросов второго раздела курса n2= 40, а количество выученных вопросов этого раздела (т.е. благоприятствующих хорошему ответу) т2 = 25.
Далее введём обозначения следующих событий:
А - событие, состоящее в том, что студент знает ответ на вопрос, случайным образом предложенный ему из первого раздела курса;
 - противоположное событие, состоит в том, что студент не знает ответ на вопрос, случайным образом предложенный ему из первого раздела курса.
- противоположное событие, состоит в том, что студент не знает ответ на вопрос, случайным образом предложенный ему из первого раздела курса.
 Событие В состоит в том, что студент знает ответ на вопрос, случайным образом предложенный ему из второго раздела курса;
Событие В состоит в том, что студент знает ответ на вопрос, случайным образом предложенный ему из второго раздела курса;
В – противоположное событие, состоит в том, что студент не знает ответ на вопрос, случайным образом предложенный ему из второго раздела курса.
Вероятности событий А и В найдём, пользуясь классическим определением вероятности:
 .
.
Вероятности противоположных событий  и
и  определим, исходя из соотношения между вероятностями противоположных событий:
определим, исходя из соотношения между вероятностями противоположных событий:

1) Для нахождения ответа на первый пункт введем обозначение ещe одного события: пусть событие С состоит в том, что студент знает ответы на оба случайным образом предложенных ему вопроса из первого и второго разделов курса.
Опираясь на понятие произведения двух событий, видим, что  .
.
Для нахождения вероятности события С применим теорему умножения вероятностей независимых событий, состоящую в том, что вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий:

2) Для решения второго пункта задачи введем еще одно обозначение события: событие D состоит в том, что студент не знает ответы на оба случайным образом предложенных ему вопроса из первого и второго разделов.
Опираясь на понятие произведения двух событий, получаем, что  .
.
Для нахождения вероятности события D применим еще раз теорему умножения вероятностей независимых событий:

3) Для решения третьего пункта введем ещё одно обозначение события: событие Е состоит в том, что студент знает ответ только на один из двух случайным образом предложенных ему вопросов из первого или второго разделов курса, причем безразлично на какой именно—первый или второй.
Это сложное событие может проявиться в виде двух несовместных вариантов: или студент знает ответ на вопрос из первого раздела и не знает ответ на вопрос из второго раздела, т.е.  ; или же студент не знает ответ на вопрос из первого раздела и знает ответ на вопрос из второго раздела, т.е.
; или же студент не знает ответ на вопрос из первого раздела и знает ответ на вопрос из второго раздела, т.е.  .
.
Таким образом, событие  .
.
Для нахождения вероятности этого события применим теорему сложения вероятностей несовместимых событий, говорящую о том, что вероятность появления одного из двух несовместимых событий А и В, безразлично какого, равна сумме вероятностей этих событий.
Отсюда получаем

Применяя к каждому из слагаемых теорему умножения вероятностей, получаем:
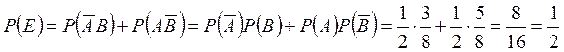
Ответ: 1) Студент знает ответы на оба предложенных опроса с вероятностью  .
.
2) Студент не знает ответ на оба предложенных вопроса с вероятностью  .
.
3) Студент знает ответы на один из двух предложенных ему вопроса с вероятностью  .
.
Пример 2.
Вероятность безотказной работы в течение гарантированного срока составляет для пылесоса 0,8 и для холодильника 0,95.
Какова вероятность того, что в течение гарантийного срока окажется работоспособным хотя бы один прибор?
Решение.
Введём обозначение событий:
событие А состоит в том, что пылесос не сломается в течение гарантийного срока;
 - противоположное событие, состоит в том, что пылесос сломается в течение гарантийного срока;
- противоположное событие, состоит в том, что пылесос сломается в течение гарантийного срока;
событие В состоит в том, что холодильник не сломается в течение гарантийного срока;
 - противоположное событие, состоит в том, что холодильник сломается в течение гарантийного срока.
- противоположное событие, состоит в том, что холодильник сломается в течение гарантийного срока.
Вероятности событий А и В известны из условия задачи: Р(А)=0,80; Р(В) = 0,95.
Вероятности противоположных событий  и
и  определим, исходя из соотношения между вероятностями противоположных событий:
определим, исходя из соотношения между вероятностями противоположных событий:

Обозначим интересующее нас событие через D.
По теореме «про хотя бы» имеем:
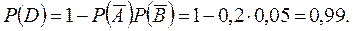
Ответ: Вероятность того, что хотя бы один из приборов будет работать в течение гарантийного срока 
Пример 3.
Магазин получил две равные по количеству партии обуви в одинаковых упаковках. Известно, что в среднем 8% обуви в первой партии и 14% во второй партии имеют определённые дефекты отделки верха. Какова вероятность того, что взятая наугад в магазине пара обуви будет иметь дефект отделки верха?
Решение.
Эта задача решается с применением формулы полной вероятности.
Введём обозначение событий. Пусть:
событие А состоит в том, что наугад выбранная пара обуви имеет дефект отделки верха;
событие H1 состоит в том, что наугад выбранная пара обуви взята из первой партии;
H2 состоит в том, что наугад выбранная пара обуви взята из второй партии.
Вероятность события А найдём, пользуясь формулой полной вероятности:

Так как по объёму обе партии одинаковые, то вероятности Р(H1) и Р(H2) равны между собой и Р(H1)=Р(H2)=0,5.
 - условная вероятность того, что наугад взятая пара обуви из первой партии имеет дефект отделки верха. По условию задачи
- условная вероятность того, что наугад взятая пара обуви из первой партии имеет дефект отделки верха. По условию задачи 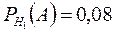 .
.
 - условная вероятность того, что наугад взятая пара обуви из второй партии имеет дефект отделки верха.
- условная вероятность того, что наугад взятая пара обуви из второй партии имеет дефект отделки верха.
По условию задачи  .
.
Подставляем все вероятности в формулу полной вероятности:
 .
.
Ответ: Вероятность того, что наугад выбранная пара обуви имеет дефект отделки верха, равна Р(А) = 0,11.
Пример 4.
Покупатель может приобрести нужный ему товар в двух магазинах. Вероятность обращения в эти магазины: 0,3 - в первый и 0,7-во второй.
Вероятность того, что к моменту прихода покупателя нужный товар уже распродан, равна 0,2 для первого и 0,6 для второго магазинов.
Покупатель посетил один из магазинов и приобрёл нужный ему товар. Какова вероятность того, что он купил его именно в первом магазине?
Решение
Эта задача решается с применением формул полной вероятности и Бейеса.
Введём обозначение событий. Пусть:
событие А состоит в том, что покупатель приобрёл нужный ему товар;
событие H1 состоит в том, что покупатель посетил первый магазин;
событие H2 состоит в том, что покупатель посетил второй магазин.
1) Вероятность события А найдём, пользуясь формулой полной вероятности:
 .
.
Вероятности гипотез H1 и H2 нам заданы в условии задачи:
Р(H1)=0,3; Р(H2)=0,7.
 - условная вероятность того, что к моменту прихода покупателя в первый магазин там есть нужный ему товар.
- условная вероятность того, что к моменту прихода покупателя в первый магазин там есть нужный ему товар.
По условию задачи  .
.
 - условная вероятность того, что к моменту прихода покупателя во второй магазин там есть нужный ему товар.
- условная вероятность того, что к моменту прихода покупателя во второй магазин там есть нужный ему товар.
По условию задачи  .
.
Подставляем все вероятности в формулу полной вероятности:
 .
.
2) Вероятность того, что необходимый товар покупатель приобрёл именно в первом магазине, найдём, пользуясь формулой Бейеса:

Подставляя сюда все найденные вероятности, получим:
 .
.
Ответ: Вероятность того, что необходимый товар покупатель приобрёл именно в первом магазине, равна РА(Н1)= 0,4615.
Пример 5.
В таблице приведен закон распределения Р(Х=хi) = рi, дискретной случайной величины. Требуется:
а) проверить, действительно ли значения, представленные в таблице, являются законом распределения дискретной случайной величины;
б) определить математическое ожидание М (х), дисперсию D(x) и  среднее квадратичное отклонение этой дискретной случайной величины;
среднее квадратичное отклонение этой дискретной случайной величины;
в) построить график этого закона распределения вероятностей.
| X | ||||
| pi | 0,29 | 0,41 | 0,21 | 0,09 |
Решение
а) Чтобы значения, представленные в таблице, являлись законом распределения дискретной случайной величины, должны быть выполнены два условия:
1) значения xi, следуют в строго возрастающем порядке;
2) сумма всевозможных вероятностей рi, равна единице, т.к. в таблице представлены все возможные значения дискретной случайной величины и они образуют полную группу событий:
 .
.
Проверяем их выполнение.
Условие 1) выполнено: значения xi дискретной случайной величины расположены в строго возрастающей последовательности - 0, 1, 2, 3.
Проверяем второе условие:
 .
.
Вычисляем сумму вероятностей, стоящих во второй строке:
 .
.
Второе условие тоже выполнено.
Значит, в таблице действительно приведен закон распределения дискретной случайной величины.
б) Находим основные характеристики заданной дискретной случайной величины.
1) Определим математическое ожидание или среднее значение дискретной случайной величины:


Итак, математическое ожидание  .
.
2) Для нахождения дисперсии по формуле D(x) = М (х2) - а2 необходимо сначала найти М(х2) - среднее значение квадрата этой случайной величины. Запишем закон распределения квадрата случайной величины xi2:
| X | ||||
| pi | 0,29 | 0,41 | 0,21 | 0,09 |
Определим математическое ожидание или среднее значение квадрата дискретной случайной величины xi2:

Находим дисперсию:
D(X) = M(x2)-a2 = 2,06-(1,10)2 = 2,06-1,21 = 0,85.
3) Вычисляем среднее квадратичное отклонение  , характеризующее средний разброс значений хi дискретной случайной величины вокруг ее среднего значения а. Оно равно корню квадратному из дисперсии:
, характеризующее средний разброс значений хi дискретной случайной величины вокруг ее среднего значения а. Оно равно корню квадратному из дисперсии:
 .
.
в) Построим график распределения случайной величины. Для этого по оси абсцисс откладываем значения заданной случайной хi =0; 1; 2; 3, а по оси ординат - соответствующие им вероятности рi.

Рис.1. График распределения случайной величины.
Ответ: а) Заданная в условии задачи таблица представляет закон распределения дискретной случайной величины.
б) Математическое ожидание этой случайной величины  ; её дисперсия D(x) = 0,85; среднее квадратичное отклонение
; её дисперсия D(x) = 0,85; среднее квадратичное отклонение  .
.
| <== предыдущая | | | следующая ==> |
| Алгоритм действий при изменении качества воды централизованного водоснабжения на объектах стационарной сети. | | | https://vk.com/club110965642 |
Date: 2016-07-18; view: 1462; Нарушение авторских прав