
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Соответствие между числами систем счисления
|
|
Практическая работа № 3.
Тема: «Арифметические и логические основы работы компьютера»
Цель: Формирование представлений об основных системах счисления (десятичной, двоичной, восьмеричной, шестнадцатеричной). Изучить, как осуществляется перевод между этими системами счисления. Изучение логических основ компьютера, основ алгебры логики. Построение таблиц истинности для сложных высказываний.
Теоретический материал:
Система счисления — это способ записи чисел с помощью фиксированного числа знаков.
Соответствие между числами систем счисления

Запись чисел в каждой из систем счисления с основанием q означает сокращенную запись выражения:
an-1 qn-1 + an-2 qn-2+... + a1 q1 + a0 q0 + a-1 q-1 +... + a-m q-m,
где ai - цифры системы счисления; n и m - число целых и дробных разрядов соответственно.
Перевод числа из одной системы счисление в другую
Перевод восьмеричных и шестнадцатеричных чисел в двоичную систему: надо каждую цифру заменить эквивалентной ей двоичной триадой (тройкой цифр) или тетрадой (четверкой цифр).
Примеры: 2538= 10 101 0112, 2D16= 10 11012.
Чтобы перевести число из двоичной системы в восьмеричную или шестнадцатеричную, его нужно разбить влево и вправо от запятой на триады (для восьмеричной) или тетрады (для 16-ричной) и каждую такую группу заменить соответствующей восьмеричной (шестнадцатеричной) цифрой. Если в старшей (т.е. самой левой) группе битов не хватает, их можно дополнить слева незначащими нулями.
Примеры: 110102 = 0001 1010 = 1A16, 110101100012= 011 010 110 0012=32618.
При переводе целого десятичного числа в систему с основанием q его необходимо последовательно делить на q до тех пор, пока не останется остаток, меньший или равный q-1. Число в системе с основанием q записывается как последовательность остатков от деления, записанных в обратном порядке, начиная с последнего.
Пример: перевод числа 2010 в двоичный код: (20)10 = (10100)2.

При переводе числа из двоичной (восьмеричной, шестнадцатеричной) системы в десятичную надо это число представить в виде суммы степеней основания его системы счисления.
Пример: (10100)2 = 1*24 + 0*23 + 1*22 + 0*21 + 0*20 = 16+4 =(20)10.
Перевод пpавильной десятичной дpоби в другую позиционную систему счисления.
1) последовательно умножать данную дробь на основание системы счисления, в которую переводим, до тех пор, пока дробная часть не будет равна нулю, или не будет достигнута требуемая точность вычислений. При этом необходимо выделять целые части получаемых произведений;
2) полученные целые части произведений, являются цифрами числа в новой системе счисления (при необходимости их надо привести в соответствие с алфавитом этой системы счисления);
3) составить дробную часть в новой системе счисления начиная с целой части первого произведения.
Пример. Перевести число 0,6562510 в восьмеричную систему счисления.

0,6562510 = 0,528
Арифметические операции в двоичной системе счисления
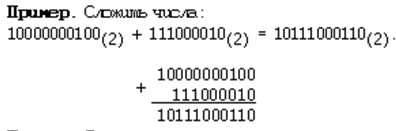 Для сложения чисел в двоичной системе используют следующие правила:*
Для сложения чисел в двоичной системе используют следующие правила:*
0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 10
Для умножения чисел в двоичной системе используют следующие правила:
0 * 0 = 0
1 * 0 = 0
1 * 1 = 1.

Алгебра логики
| Обозначение | Операция | Таблица истинности | Перевод на естественный язык |
| A Ù B, A & B A * B, | логическое умножение (конъюнкция) |  
| A и В |
| A Ú B A + B | логическое сложение (дизъюнкция) |  
| A или В |
А, 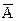 ,
Not A ,
Not A
| Отрицание (инверсия) | 
| не А |
| A → B | следование (импликация) | 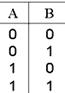 
| Если A, то В |
| А«В | равносильность (эквивалентность) |  
| А тогда и только тогда, когда В |
| Приоритет операции | Логическая операция |
| Первый (высший) | Логическое отрицание |
| Второй | Конъюнкция (логическое умножение) |
| Третий | Дизъюнкция (логическое сложение) |
| Четвертый | Импликация (следование) |
| Пятый (низший) | Эквивалентность (равносильность) |
Вопросы для отчета:
1. Переведите числа из десятичной системы счисления в восьмеричную:
Вариант 1 а) 37,41; б) 2936.
Вариант 2 а) 47,54; б) 2537.
Вариант 3 а) 56,49; б) 2846.
Вариант 4 а) 66,53; б) 2796.
Вариант 5 а) 46,78; б) 3976.
Вариант 6 а) 87,32; б) 2645.
2. Переведите числа из десятичной системы счисления в шестнадцатеричную:
Вариант 1 а) 25,25; б) 43,78.
Вариант 2 а) 65,33; б) 23,48
Вариант 3 а) 21,24; б) 83,85
Вариант 4 а) 33,45; б) 53,29
Вариант 5 а) 77,65; б) 93,24
Вариант 6 а) 57,68; б) 38,51
3. Переведите числа из десятичной системы счисления в двоичную:
Вариант 1 а) 40,5; б) 31,75; в) 124,25.
Вариант 2 а) 41,25; б) 32,65; в) 134,75.
Вариант 3 а) 42,7; б) 33,85; в) 104,5.
Вариант 4 а) 43,35; б) 34,8; в) 130,25.
Вариант 5 а) 44,65; б) 37,5; в) 137,15.
Вариант 6 а) 45,75; б) 39,6; в) 145,25.
4. Переведите десятичные дроби в двоичную систему счисления (ответ записать с шестью двоичными знаками):
Вариант 1 а) 0,4622; б) 0,5803.
Вариант 2 а) 0,4533; б) 0,5207.
Вариант 3 а) 0,4744; б) 0,5645.
Вариант 4 а) 0,4855; б) 0,5716.
Вариант 5 а) 0,4966; б) 0,5328.
Вариант 6 а) 0,4411; б) 0,5467.
5. Переведите двоичные числа в шестнадцатеричную систему счисления:
Вариант 1 а) 1110,01010001; б) 100,1111001.
Вариант 2 а) 1010,01110101; б) 110,1101101.
Вариант 3 а) 1001,01010111; б) 101,1100011.
Вариант 4 а) 1000,00010011; б) 111,1110011.
Вариант 5 а) 1101,01011101; б) 1010,1010101.
Вариант 6 а) 1100,01110100; б) 1011,1101001.
6. Переведите восьмеричные и шестнадцатеричные числа в двоичную систему счисления:
Вариант 1 а) 12708; б) 10,2316.
Вариант 1 а) 12358; б) 50,3216.
Вариант 1 а) 16328; б) 20,1216.
Вариант 1 а) 13978; б) 30,3116.
Вариант 1 а) 21768; б) 40,4116.
Вариант 1 а) 52438; б) 60,2416.
 7.
7.
| <== предыдущая | | | следующая ==> |
| Тема: «Правовые нормы, относящиеся к информации». | | | Задание 1.5 Put the verbs in the Past Tense |
Date: 2016-07-18; view: 1259; Нарушение авторских прав