
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Основная теорема зацепления
|
|
Рассмотрим тела 1 и 2, совершающие вращательные движения, соответственно вокруг центров 01 и 02 с угловыми скоростями w1 и w2, и образующих между собой высшую кинематическую пару А (рис. 5.9).
Общая нормаль n-n профилей в точке контакта А пересекает линию межцентрового расстояния 0102 точке Р, называемой полюсом зацепления, и в кинематическом отношении, являющейся центром мгновенного вращения в относительном движении звеньев высшей кинематической пары.
В плоском механизме обеспечении передачи заданного движения зависит от геометрии сопряженных профилей (I и II на рис. 5.9). Часто на практике геометрию сопряженных профилей подбирают так, чтобы она обеспечивала закон движения, характеризуемый постоянством передаточного отношения между звеньями 1 и 2 высшей пары, т.е. i 12 = const.
В рассматриваемый момент времени скорости точки А равны:
- в системе колеса 1:  ,
,
- в системе колеса 2: 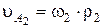 ,
,
где r1 и r1 – радиус векторы (расстояния соответственно от центов вращения 01 и 02 до точки А).
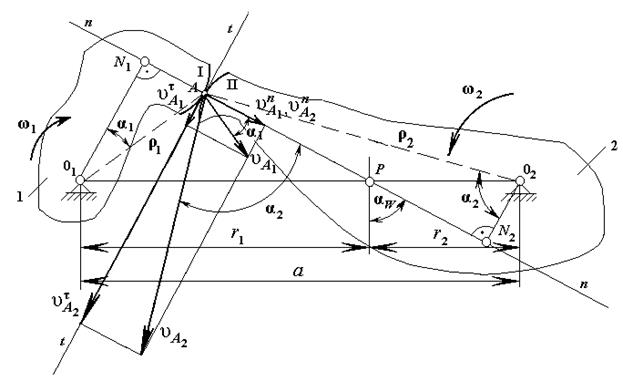
Рис. 5.9
Проекции 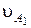 и
и 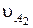 на нормаль n-n должны быть равны:
на нормаль n-n должны быть равны:
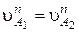 ®
® 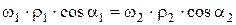 (1)
(1)
Иначе, или зубья будут внедряться один в другой, или колеса выйдут из зацепления.
Проекции  и
и  на касательную t-t не равны между собой, поэтому в высшей кинематической паре возникает проскальзывание профилей.
на касательную t-t не равны между собой, поэтому в высшей кинематической паре возникает проскальзывание профилей.
Проецируем центры вращения 01 и 02 на нормаль n-n получаем точки N 1 и N 2. Из треугольника D 01 N 1 А:  . Из треугольника D 02 N 2 А:
. Из треугольника D 02 N 2 А: 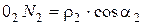 .
.
Следовательно, с учетом выражения 1: 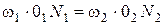 ,
,
или 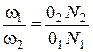 .
.
Рассматривая треугольники D 01 РN 1 и D 02 РN 2, устанавливаем, что они подобные (имеют три стороны взаимно параллельные друг другу), составляем пропорцию:
 ,
,
где r 1 и r 2 – радиусы начальных окружностей. Если они используются в качестве производственных окружностей в процессе нарезания колес, то они получают ещё название делительных окружностей.
Следовательно передаточное отношение в общем виде может быть записано:
 ® основная теорема зацепления.
® основная теорема зацепления.
Т.е. общая нормаль n-n к соприкасающимся (сопряженным) профилям зубьев делить межосевое расстояние 0102 на части обратно пропорциональные угловым скоростям (передаточному отношению). Следовательно, для обеспечения постоянства передаточного отношения контактирующие участки профилей должны быть очерчены по таким кривым, чтобы в любой момент соприкосновения их общая нормаль в точке контакта проходила через одну и ту же точку Р (полюс зацепления), на линии центров, т.е. полюс зацепления в процессе перекатывания зубьев не меняет своего положения.
Межосевое расстояние можно определить:
 , или
, или 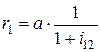 ;
;  .
.
Угол aW, составленный общей нормалью n-n к профилям зубьев (линией зацепления) и общей касательной к начальным окружностям, называют углом зацепления.
Для рассмотрения относительного движения тел используем метод обращения движения (метод мысленной остановки), т.е. сообщим всем звеньям системы вращательное движение вокруг оси 01 с угловой скоростью w1 в направлении, противоположном первоначальному. Тогда 1-е звено остановится, второе будет совершать сложное плоскопараллельное движение, состоящее из вращения вокруг осей 01 и 02 одновременно, а его движение по отношению к неподвижному первому телу можно рассматривать, применяя метод мгновенных центров скоростей (известный из теоретической механики).
Окружные скорости точек, лежащих на начальных окружностях r 1 и r 2, всегда равны, следовательно, если первая окружность остановлена, то вторая будет катиться по первой без скольжения, а точка Р станет мгновенным центром скоростей второго тела. Для определения мгновенной скорости w запишем скорость оси 02 в виде равенства:
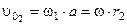 .
.
Так как  , а
, а  , то:
, то:
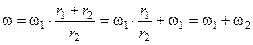 .
.
Итак, после остановки первого тела второе будет вращаться вокруг полюса с мгновенной угловой скоростью 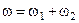 . Отсюда следует, что точка А контакта второго тела будет скользить по поверхности первого тела со скоростью,
. Отсюда следует, что точка А контакта второго тела будет скользить по поверхности первого тела со скоростью,
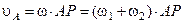 ,
,
которую называют скоростью скольжения контактных точек. Скольжение контактных точек сопровождается трением.
Требованиям основной теоремы зацепления удовлетворяют различные кривые, но наибольшее распространение получили: эвольвентное, круговое (зацепление М.Л. Новикова) и циклоидальное.
Геометрические параметры зубчатых колёс
При проектировании зубчатого колеса вначале нужно определить его число зубьев Z, а затем определить параметры зубьев.
Основным параметром зацепления является шаг р – расстояние между двумя одноименными точками двух соседних профилей зубьев измеренное по делительной окружности (рис. 5.10):
 ,
,
где s – толщина зуба; sв – ширина впадины.
Величина 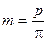 , мм называется модулем зацепления.
, мм называется модулем зацепления.
Получим формулу для определения радиуса делительной окружности r w. Длина делительной окружности колеса равна:
 , или в шагах
, или в шагах 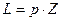 .
.
Отсюда: 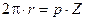 ®
® 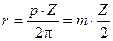 .
.
| n ra s sв N p ry t ay n r rf 0 rb Рис. 5.10 |
Делительная окружность – это окружность для которой шаг дает в пересчете стандартное значение модуля.
Для нормальных колес находящихся в зацеплении делительные окружности совпадают с начальными r = r w.
Делительная окружность делит зуб на головку и ножку. Высота зуба равна:
h = h ¢ + h ²,
где h ¢ – высота головки зуба, h ¢ = m; h ² - высота ножки зуба, h ² = 1,25× m.
Полная высота зуба h =2,25× m.
Отсюда радиус окружности выступов:
 .
.
Радиус окружности впадин:
 .
.
Передаточное отношение зубчатой передачи можно определить используя основную теорему зацепления:
 ,
,
Для зубчатых механизмов существует еще одна характеристика – передаточное число: отношение зубьев большего колеса к числу зубьев меньшего колеса:
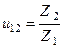 , (т.е. всегда положительное).
, (т.е. всегда положительное).
Межосевое расстояние при внешнем зацеплении колес:
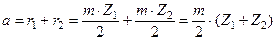
На колесе можно провести бесчисленное число окружностей на каждой из которых будет свой модуль. Для ограничения этого числа ГОСТом введен стандартный ряд модулей. Стандартной модуль определяется по окружности называемой делительной. Точнее делительной называется такая окружность зубчатого колеса, на которой модуль и шаг принимают стандартное значение. Окружным шагом или шагом называется расстояние по дуге окружности между одноименными точками профилей соседних зубьев (под одноименными понимаются правые или левые профили зуба). Угловой шаг t - центральный угол соответствующий дуге p - окружному шагу по делительной окружности.
Примечание: Согласно ГОСТ основные элементы зубчатого колеса обозначаются по следующим правилам: линейные величины - строчными буквами латинского алфавита, угловые - греческими буками; установлены индексы для величин:
· по окружностям: делительной - без индекса, вершин - a, впадин - f, основная - b, начальная - w;
· по сечениям: нормальное сечение - n, торцевое сечение - t, осевое сечение - x;
· относящихся к зуборезному инструменту - 0.
Радиус основной окружности для эвольвенты:
rb = r× cos a.
где a - угол профиля на делительной окружности,
Углом профиля называется острый угол между касательной к профилю в данной точки и радиусом - вектором, проведенным в данную точку из центра колеса.
Контрольные вопросы
12. Проанализируйте достоинства и недостатки фрикционной передачи?
13. Что такое фрикционный вариатор скорости?
14. Назовите основные виды зубчатых механизмов?
15. Сформулируйте и докажите основную теорему зацепления?
16. Что называется шагом зацепления?
17. Что называется модулем зацепления, зачем его гостируют?
18. Чему равен диаметр делительной окружности?
19. Чему в долях модуля равна высота ножки и головки зуба нормального колеса?
Лекция 6
Сложные зубчатые передачи. Передаточное отношение передач с промежуточными колесами и валами. Планетарные механизмы. Формула Виллиса. Кинематическое исследование типовых планетарных механизмов аналитическим методам.
Сложные зубчатые механизмы
В большинстве современных машин и приборов возникает необходимость осуществлять передачу вращения от ведущего вала к ведомому с большим передаточным отношением (при значительных межосевых расстояниях) и строгом согласовании скоростей вращения отдельных валов. В этом случае применяют зубчатые механизмы либо замедляющие (wведущего > wведомого), так называемые редукторы, либо ускоряющие (wведущего < wведомого) - мультипликаторы. Такие механизмы обладают одной степенью свободы (лекция 5, рис 5.4, а, б). Так как в машиностроении чаще возникает необходимость в уменьшении скоростей вращения, то замедляющие механизмы (или редукторы) нашли более широкое применение на практике. Использование их в машиностроении позволяет применять быстроходные, а следовательно, малогабаритные и более дешевые двигатели (электро-, турбо и прочие двигатели) при тихоходных рабочих машинах, малые скорости движения которых обусловливается требованиями технологического или рабочего процессов. В приборостроении применение понижающих передач обеспечивает малые перемещения измеряющих или регулирующих элементов (получение более точной настройки прибора или установки вводимой в него величины - индикаторы, тахометры и др.), повышающие передачи применяют для расширения шкалы и более точного отсчета замеряемой величины. Однако ускоряющие механизмы (мультипликаторы) применяют значительно реже и главным образом там, где передаточное отношение изменяется в пределах от -1 до +1. У редукторов передаточное отношение может изменяться в очень широком диапазоне (до сотен и даже нескольких тысяч). Но осуществлять большие передаточные отношения с помощью простейшего зубчатого механизма (одноступенчатого, два колеса и стойка), нецелесообразно, так как в этом случае получаются большие размеры механизма. Кроме того, при высоких значениях передаточного отношения в одной паре колес зубья малого колеса входят в контакт значительно большее число раз, чем зубья большого колеса, вследствие чего они изнашиваются быстрее. Поэтому с точки зрения уменьшения габаритов, повышения долговечности и улучшения условий не принудительной смазки делать в одной паре зубчатых колес передаточное отношение больше 6¼8 конструктивно нерационально.
В тех случаях, когда заданное передаточное отношение превышает целесообразное для одной пары колес или когда требуется обеспечить большое межосевое расстояние, используют сложные зубчатые механизмы, состоящие из нескольких параллельно или последовательно соединенных друг с другом зубчатых передач. Различают два вида таких механизмов: сложные зубчатые механизмы с неподвижными осями (многократные зубчатые передачи лекция 5, рис 5.8, а) и планетарные (эпициклические) зубчатые механизмы (оси отдельных колес могут перемещаться относительно стойки, как на рис 5.8, б, в лекции 5). Каждый из этих видов сложных зубчатых механизмов может быть составлен не только из однородных колес (цилиндрических или конических) и передач (с неподвижными осями или планетарных), но и из их сочетания (рис. 6.1). Наибольшее распространение получили сложные зубчатые механизмы, составленные из цилиндрических колес с прямыми зубьями (реже косыми) с равноделенным шагом. Если у зубчатых механизмов оси ведущего и ведомого звеньев располагаются по одной прямой (рис 5.8, б, в), то они называются соосными.
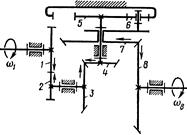
Рис. 6.1
Общее передаточное отношение любого типа сложного зубчатого механизма i 1 n, включающего несколько последовательно соединенных друг с другом простых механизмов (не планетарных ступеней, планетарных или их комбинаций) из n колес, равно произведению передаточных отношений отдельных простых механизмов (ступеней), входящих в его состав, т.е.:
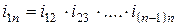 ,
,
Так, для механизма, представленного на рис. 6.1, состоящего из ступени цилиндрической передачи с колесами 1-2 с неподвижными осями, конической передачи 3-4, планетарной ступени 5-6-7, конической передачи с неподвижными осями 7-8, общее передаточное отношение равно:
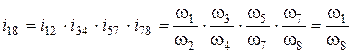
так как w2 = w3; w4 = w5.
Степень подвижности механизмов с неподвижными осями колес равна единице, благодаря чему соотношение между угловыми скоростями ведущего и ведомого звеньев остается постоянным. Поэтому в задачу исследования этих механизмов входит определение передаточного отношения по заданной схеме и размерам колес. При этом колеса на схемах сложных зубчатых механизмов изображаются полоидными или совпадающими с ними начальными окружностями. Планетарные механизмы могут иметь две и более степени свободы. В этом случае соотношения между угловыми скоростями выходных валов будут неоднозначными. Определение угловых скоростей колес таких механизмов при различных режимах работы является основной задачей их исследования.
Проектирование любых зубчатых механизмов обязательно состоит из двух этапов: выбора структурной и кинематической схем механизма и определение чисел зубьев для обеспечения требуемого передаточного отношения.
Кинематическое исследование механизмов
Исследование рядовых зубчатых механизмов
Рядовые зубчатые механизмы (передачи с промежуточными или паразитными колесами), представляют собой последовательное соединение нескольких пар зубчатых колес, на каждой из неподвижных осей которых помещено по одному колесу (рис. 6.2). Имея схему передачи и зная числа зубьев или радиусы полоидных окружностей колес, можно определить общее передаточное отношение редуктора аналитически или графически.
Для механизма, состоящего из четырех последовательно соединенных цилиндрических колес внешнего зацепления (рис. 6.2), общее передаточное отношение:
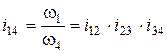
где i 12 - передаточное отношение первой пары сцепляющихся зубчатых колес внешнего зацепления:

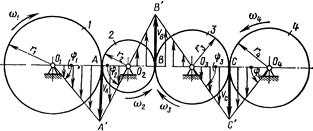
Рис. 6.2
Знак минус поставлен потому, что колеса 1 и 2 вращаются в противоположных направлениях. Для второй пары:

Для третьей пары:
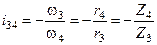 ,
,
Тогда искомое передаточное отношение:

В общем случае при n колесах в механизме:
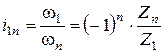
Общее передаточное отношение рядового зубчатого механизма равно обратному отношению чисел зубьев или радиусов крайних колес. Знак передаточного отношения определяется множителем (-1) n, где n - число передач внешнего зацепления. При n четном i > 0, т.е. ведомое и ведущее звенья редуктора или мультипликатора вращаются в одном направлении; при нечетном n - в разных направлениях.
Анализируя приведенные примеры устанавливаем, что число зубьев промежуточных колес 2 и 3, находящихся одновременно в зацеплении с двумя другими колесами, не влияет на величину общего передаточного отношения механизма. Но установка таких промежуточных колес позволяет изменять направление вращения ведомого звена. При четном числе промежуточных колес направление вращения ведущего и ведомого звеньев противоположны, при нечетном - одинаковы. Применяют эти колеса главным образом там, где необходимо изменить направление вращения ведомого вала при неизменном направлении вращения ведущего (механизм трензеля токарного станка, механизм заднего хода автомобильной коробки передач и др.), либо там, где необходимо обеспечить передачу движения при больших межосевых расстояниях (когда нельзя увеличивать размеры ведущих и ведомых колес из-за их больших габаритов).
Исследование зубчатых механизмов с промежуточными валами
Сложные зубчатые механизмы с промежуточными валами представляют собой последовательное соединение нескольких пар колес, на каждый из валов которого помещено более одного колеса (кроме валов ведущего и ведомого колес). На рис. 6.3 представлен такой трёхступенчатый механизм для преобразования движения между параллельными валами, который состоит из двух ступеней внешнего зацепления с цилиндрическими колесами (1-2 и 3-4) и одной ступени внутреннего о зацепления (колеса 5-6). Колеса 2-3 и 4-5 соединены вместе, образуя звенья.
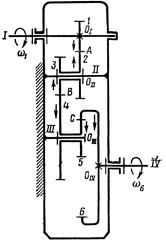
Рис. 6.3
Передаточное отношение первой ступени равно:
 ,
,
второй:
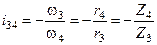
третьей:
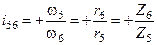
Перемножая эти значения передаточных отношений, получаем
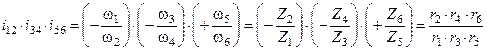
Учитывая, что, w2 = w3; w4 = w5, после сокращения получаем
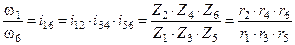
Общее передаточное отношение ступенчатой передачи равно произведению передаточных отношений ступеней, входящих в состав механизма, или равно отношению произведения чисел зубьев (полоидных радиусов) ведомых колес к произведению чисел зубьев (радиусов) ведущих колее, взятых со своими знаками. Так как передаточное отношение этого механизма (в отличие от рядового) зависит от числа зубьев всех входящих в его состав колес, то путем соответствующего подбора чисел зубьев колес можно получить большие передаточные отношения.
В общем случае при n колесах q внешних зацеплений, общее передаточное отношение равно:

В случае соосного механизма, составленного из нулевых колес (рис. 6.4) должно удовлетворяться условие соосности (равенство межосевых расстояний):
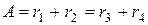 ,
,
или
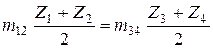 ,
,
где m 12 и m 34 - соответственно модули зацеплений первой и второй ступеней.

Рис. 6.4
Планетарные механизмы
Сложные зубчатые механизмы, в которых ось хотя бы одного колеса подвижна, называются планетарными механизмами. К типовым планетарным механизмам относятся:
· однорядный планетарный механизм;
· двухрядный планетарный механизм с одним внешним и одним внутренним зацеплением;
· двухрядный планетарный механизм с двумя внешними зацеплениями;
· двухрядный планетарный механизм с двумя внутренними зацеплениями.
Элементы планетарного механизма имеют специальные названия:
· зубчатые колеса оси которых неподвижны называются центральными. Колесо с внешними зубьями, расположенное в центре механизма называется солнечным, колесо с внутренними зубьями называют короной или эпициклом;
· колеса, оси которых подвижны, называют планетными или сателлитами;
· подвижное звено, соединяющее оси центральных колес и сателлитов называют водилом. Водило принято обозначать не цифрой, а латинской буквой h, или русской в.
В таблице 6.1 приведены структурные схемы типовых планетарных механизмов, а также диапазоны рекомендуемых передаточных отношений и ориентировочные значения КПД при этих передаточных отношениях.
Таблица 6.1 Типовые схемы планетарных механизмов
| № | Структурная схема механизма | u | h |
           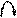 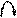            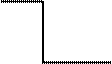       1. 1.
| 2 3 1 в w1w в | 3…10
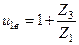
| 0,97…0,99 |
| 2 3 1 в w1w в | 7…16
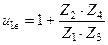
| 0,96…0,98 | |
                          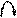 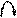     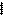   3 3
| 2 3 1 в w 1 w в | 25…300

| 0,9…0,3 |
 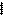                    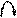  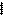         4 4
| 2 3 1 в w 1 w в | 30…300

| 0,9…0,3 |
Если степень подвижности планетарного механизма 2 и более, то его называют дифференциальным. Для механизма выполненного по схеме 1 табл. 6.1 степень подвижности при закреплённом колесе 3 равна:
W = 3× (4 – 1) - 2×3 – 1× 2 = 1.
При свободном колесе 3:
W = 3× (5 – 1) - 2×4 – 1× 2 = 2.
Достоинства планетарных механизмов: большие передаточные отношения при малых габаритных размерах; можно применять для сложения, или разделения движения.
Метод Виллиса (аналитический метод кинематического анализа)
Метод Виллиса основан на способе обращения движения (способ мысленной остановки водила): всем звеньям механизма мысленно придаем вращение с угловой скоростью равной угловой скорости водила, только в обратном направлении. Относительные движения звеньев при этом не изменяются, абсолютные будут следующими (для схемы 1, табл. 6.1):
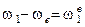 ,
,
 ,
,
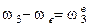 ,
,
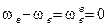 .
.
Расшифруем принятые обозначения: w1, w2, w3, w в – истинные значения угловых скоростей звеньев; 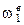 - угловая скорость центрального колеса 1 при остановленном водиле;
- угловая скорость центрального колеса 1 при остановленном водиле; 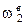 - угловая скорость сателлита 2 при остановленном водиле;
- угловая скорость сателлита 2 при остановленном водиле; 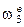 - угловая скорость центрального колеса 3 при остановленном водиле (равна - w в);
- угловая скорость центрального колеса 3 при остановленном водиле (равна - w в);  - угловая скорость водила при остановленном водиле (равна нулю).
- угловая скорость водила при остановленном водиле (равна нулю).
Тогда получаем, что все колеса совершают вращательные движения вокруг неподвижных осей и общее передаточное отношение можно найти по формуле:
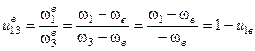 ® формула Виллиса.
® формула Виллиса.
После применения метода обращения движения, рассматриваемый механизм можно рассматривать как сложный двухступенчатый с промежуточным колесом:
 ,
,
тогда:
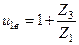 .
.
Контрольные вопросы
20. Почему при определении передаточного отношения зубчатого сложного механизма с промежуточными колесами можно не учитывать количество зубьев промежуточных колес?
21. Что такое промежуточный вал?
22. Дайте характеристику звеньев входящих в планетарный механизм?
23. Выведите формулу Виллиса для анализа планетарного механизма?
Лекция 7
Проектирование планетарных зубчатых механизмов. Постановка задачи синтеза. Условия подбора чисел зубьев. Вывод расчетных формул для условий соосности, соседства и сборки. Задачи синтеза зацеплений. Эвольвента. Эвольвентное зацепление.
Проектирование планетарных механизмов.
Date: 2016-07-18; view: 1084; Нарушение авторских прав