Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Лекция 3 Схема Бернулли
|
|
( Тема 2.2.)
План лекции
Формула полной вероятности.
Формула Байеса.
Повторение испытаний.
Формула Бернулли.
Локальная и интегральная формулы Муавра-Лапласа в схеме Бернулли.
Определение Пусть событие А может произойти только совместно с одним из событий Н1, Н2,…, Нп, образующих полную группу несовместных событий. Тогда события Н1, Н2,…, Нп называются гипотезами.
Теорема Вероятность события А, наступающего совместно с гипотезами Н 1, Н 2,…, Нп, равна: 
где p (Hi) – вероятность i- й гипотезы, а p (A/Hi) – вероятность события А при условии реализации этой гипотезы. Данная формула носит название формулы полной вероятности.
Пример. Имеются три одинаковые урны с шарами. В первой из них 3 белых и 4 черных шара, во второй – 2 белых и 5 черных, в третьей – 10 черных шаров. Из случайно выбранной урны наудачу вынут шар. Найти вероятность того, что он белый.
Решение. Будем считать гипотезами Н 1, Н 2 и Н 3 выбор урны с соответствующим номером. Так как по условию задачи все гипотезы равновозможны, то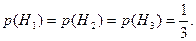 
Найдем условную вероятность А при реализации каждой гипотезы: 
Тогда 
Date: 2016-07-18; view: 270; Нарушение авторских прав