
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

ПО ДИСЦИПЛИНЕ «ЭММ».
|
|
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
ДЛЯ СТУДЕНТОВ 3 КУРСА
ФАКУЛЬТЕТА ЗАОЧНОГО ОБУЧЕНИЯ
НА 2016 УЧЕБНЫЙ ГОД
СПЕЦИАЛЬНОСТИ
Бизнес информатика
г. Симферополь, 2016 г.
Вопросы к зачету
по дисциплине «Дискретная математика»
1. Понятие множества. Основные понятия (универсальное, счетное и пустое множество). Равные и эквивалентные множества.
2. Операции над множествами: объединение, пересечение, разность дополнение. Диаграммы Венна. Примеры.
3. Понятие кортежа. Прямое (декартово) произведение множеств. Примеры.
4. Бинарное отношение (определение), его область определения и область значений, свойства (рефлексивность, симметричность, транзитивность). Отношения эквивалентности и порядка.
5. Мощности конечных множеств. Принцип включений-выключений. Примеры. Понятие о мощности бесконечных множеств.
6. Определение функции как бинарного отношения. Функция как отображение одного множества на другое. Области определения и значений функции. Примеры.
7. Основные правила комбинаторики (правило суммы и правило произведения). Примеры.
8. Комбинации элементов: размещения, сочетания, перестановки (без повторений). Формулы нахождения числа таких комбинаций. Примеры.
9. Комбинации элементов: размещения, сочетания, перестановки (с повторениями). Формулы нахождения числа таких комбинаций. Примеры.
10. Понятие высказывания. Основные логические операции (связки): отрицание, конъюнкция, дизъюнкция. Их таблицы истинности и взаимосвязь с операциями над множествами.
11. Основные логические операции (связки): импликация, эквивалентность. Их таблицы истинности и запись с помощью дизъюнкций, конъюнкций и отрицаний.
12. Понятие о производных логических операциях (связках): штрих Шеффера, стрелка Пирса, сумма по модулю два. Таблица истинности этих операций.
13. Основные свойства логических операций: идемпотентность, коммутативность, ассоциативность, дистрибутивность, Примеры.
14. Основные свойства логических операций: двойное отрицание, законы де Моргана, поглощение. Примеры.
15. Понятие о булевой алгебре; алгебра высказываний как интерпретация булевой алгебры.
16. Формулы алгебры логики и их виды: тождественно истинные, тождественно ложные и выполнимые. Примеры.
17. Булевы (логические) функции. Равенство функций. Булевы функции одной и двух переменных.
18. Дизъюнктивная нормальная форма (ДНФ) и совершенная ДНФ (СДНФ) алгебры логики и их свойства.
19. Конъюнктивная нормальная форма (КНФ) и совершенная КНФ (СКНФ) алгебры логики и их свойства.
20. Построение СДНФ и СКНФ булевой функции по таблице е истинности. Примеры. Теорема о функциональной полноте.
21. Исчисление высказываний. Понятие об алфавите, формулах, аксиомах, правилах вывода и основных теоремах исчисления высказываний.
22. Понятие предиката (высказывательной формы). Предметные переменные. Одноместные и  -местные предикаты. Тождественно истинные и тождественно ложные высказывания. Примеры.
-местные предикаты. Тождественно истинные и тождественно ложные высказывания. Примеры.
23. Операции квантор общности и квантор существования. Примеры. Свободные и связанные переменные. Выполнимые и противоречивые формулы логики предикатов.
24. Равносильные формулы логики предикатов. Примеры. Понятие об исчислении предикатов.
25. Неориентированные графы. Основные понятия: вершины и их степень, ребра, кратные ребра, петли. Матрица смежности неориентированного графа. Примеры.
26. Инцидентность. Матрица инцидентности неориентированного графа. Примеры.
27. Ориентированные графы. Матрица инцидентности орграфа. Примеры.
28. Матрица смежности орграфа. Примеры.
29. Подграфы. Полные графы. Клики. Примеры.
30. Операции над графами: дополнение, объединение и пересечение. Примеры.
31. Маршруты, циклы, цепи в неориентированных графах. Связность.
32. Деревья и их свойства. Направленные деревья.
33. Остовное дерево. Цикломатическое число. Остовное дерево минимальной нагруженности.
34. Двудольные графы. Задача о паросочетаниях.
35. Понятие алгоритма. Основные требования к алгоритмам.
36. Понятие рекурсии. Рекурсивные функции. Связь между алгоритмами и рекурсивными функциями.
Типовые задачи
по дисциплине «Дискретная математика»
Практические задачи на тему «Логические операции. Формулы логики»
Задача 1: Доказать, что формулы логически эквивалентны.
1)  и
и  .
.
2)  и
и  .
.
3) 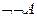 и
и  .
.
4)  и
и  .
.
5)  и
и  .
.
6)  и
и  .
.
7)  и
и  .
.
8)  и
и  .
.
9)  и
и  .
.
10)  и
и 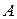 .
.
Задача 2: Доказать, что первая формула логически влечет вторую формулу.
1)  ;
;  .
.
2) 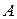 ;
; 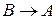 .
.
3)  ;
;  .
.
4)  ;
;  .
.
5)  ;
;  .
.
6) 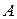 ;
;  .
.
7) 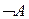 ;
;  .
.
8)  ;
;  .
.
9)  ;
;  .
.
10)  ;
;  .
.
Практические задачи на тему «Функции алгебры логики»
Задача 3: Используя таблицы истинности, проверить эквивалентность булевых формул. Определить существенные и фиктивные переменные.
1.1.  .
.
1.2. 
1.3.  .
.
Задача 4: Для булевой функции, заданной вектором значений, определить:
1) СДНФ, 2) СКНФ, 3) полином Жегалкина.
| 2.1. (10110011). |
| 2.2. (00100111). |
| 2.3. (10101011). |
Задача 5: Выяснить, является ли система функций A функционально полной.
1.4.  .
.
1.5.  .
.
1.6.  .
.
Практические задачи на тему «Множества. Операции над множествами»
Задача 6: Доказать и проиллюстрировать на примере множеств  ,
,  ,
,  тождество алгебры множеств, выражающее закон ассоциативности операции пересечения множеств.
тождество алгебры множеств, выражающее закон ассоциативности операции пересечения множеств.
Задача 7: Изобразить на координатной плоскости множества A и В точек координатной плоскости, удовлетворяющих соответственно соотношениям x2+y2 ≤1 и x2+(y-1)2 ≤1. Какие фигуры изображают множества AÈB,  ?
?
Задача 8: Доказать, что эквивалентны три предложения о произ-вольных множествах А, В и С: 1)  ; 2)
; 2)  ; 3)
; 3)  .
.
Практические задачи на тему «Бинарные отношения»
Задача 9: На множестве А ={1,2,3,4} задано отношение R ={< x; y >: x > y }. Найти область определения, область значений R. Задать матричным способом R -1; 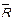 ;
;  . Указать свойства отношения.
. Указать свойства отношения.
Задача 10: На множестве N ´ N, где N – множество натуральных чисел, определим отношение r: < х, у > r < u, v > Û x + v = y + u. Доказать, что r – отношение эквивалентности на этом множестве.
Задача 11: Доказать, что отношение  является эквивалентностью на множестве
является эквивалентностью на множестве  . Какое разбиение определяет указанная эквивалентность?
. Какое разбиение определяет указанная эквивалентность?
Практические задачи на тему «Подстановки»
Задача 12: A – количество студентов; B – посещают математический кружок; C – физический; D – не посещают ни одного из кружков. Сколько студентов посещают и математический, и физический кружок? Сколько студентов посещают только математический кружок? |A|=37; |B|=20;
Задача 13: Сколькими способами из A студентов можно выбрать делегацию, если делегация состоит из B студентов? |A|=42; |B|=8.
Задача 14: Сколько имеется четырехзначных чисел, у которых каждая следующая цифра меньше предыдущей?
Задача 15: На собрании должны выступить 4 человека A,B,C,D. Сколькими способами их можно разместить в списке ораторов, если B не может выступить до того момента, пока не выступит A.
Задача 16: сколькими способами могут разместиться A покупателей в очереди в кассу. |A|=15
Практические задачи на тему «Понятие вычетов»
Задача 17: Найти такое число d ¹ 1, на которое делятся числа 6п + 5 и 9л + 2. При каком значении п. это деление возможно?
Задача 18: Для степени y=2n (n–натуральное число) установить классы сравнимости. Установить зависимость последней цифры этой степени от ее показателя.
Задача 19: Установить последнюю цифру степени y=2 2007
Практические задачи на тему «Генерирование подмножеств»
Задача 20: Сколько различных слов можно составить, переставляя буквы слова КОМБИНАТОРИКА.
Задача 21: Сколькими способами можно выбрать A одинаковых или разных пирожных в кондитерской, где есть B разных сортов пирожных. A=5; B=12
Задача 22: Пусть A={a, b, c, d, e} и B={a, b, c, f, m, k}. Указать все элементы множества AxB – декартова произведения множеств A и B.
Практические задачи на тему «Неориентированные графы»
Задача 23: По заданной матрице смежности построить неориентированный граф, составить таблицу степеней вершин, матрицу инцидентности, таблицу расстояний и условных радиусов, найти радиус и центр графа.
║ 0 0 1 0 0 1 0 0 1 ║
║ 0 0 1 0 0 1 0 0 0 ║
║ 1 1 0 1 0 0 1 0 0 ║
║ 0 0 1 0 0 1 0 0 1 ║
A(G) = ║ 0 0 0 0 0 0 0 1 1 ║
║ 1 1 0 1 0 0 0 1 0 ║
║ 0 0 1 0 0 0 0 1 0 ║
║ 0 0 0 0 1 1 1 0 1 ║
║ 1 0 0 1 1 0 0 1 0 ║
Практические задачи на тему «Ориентированные графы»
Задача 24: Задана матрица смежностиорграфа:
 .
.
Определить свойства отношения смежности вершин орграфа. Является ли орграф сильно связным? Если нет, то выделить компоненты сильной связности.
Задача 25: Найти минимальный путь из вершины v1 в v6 во взвешенном орграфе G, заданном матрицей весов:
| v 1 | v 2 | v 3 | v 4 | v 5 | v 6 | |
| v 1 | ∞ | ∞ | ||||
| v 2 | ∞ | ∞ | ∞ | ∞ | ∞ | |
| v 3 | ∞ | ∞ | ∞ | ∞ | ∞ | |
| v 4 | ∞ | ∞ | ∞ | ∞ | ∞ | |
| v 5 | ∞ | ∞ | ∞ | ∞ | ||
| v 6 | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ |
Вопросы к зачету «Теоретические основы информатики»
1. Предистория развития информатики
2. Общее представление о науке информатике
3. Объяснить смысл понятий «данные», «информация», «знание».
4. Основные свойства информации.
5. Виды информации
6. Структура информации
7. Особенности информации
8. Потребители информации
9. Информатика как наука и как вид практической деятельности.
10. Место информатики в системе наук.
11. Социальные аспекты информатики.
12. Правовые аспекты информатики.
13. Этические аспекты информатики.
14. Уровни представлений об информации
15. Непрерывная и дискретная информация.
16. Процесс передачи данных.
17. Информационные технологии.
18. Виды информационных процессов.
19. Понятие об Информационных процессах.Составляющие информационного процесса
20. Понятие информационного ресурса и информатизации, их характеристика
21. Понятие информационного объекта
22. Технические средства реализации информационных процессов.
23. Кодирование при передаче и хранении данных и информации.
24. Классификация информационных объектов.
25. Иерархическая система классификации
26. Фасетная система классификации
27. Дескрипторная система классификации
28. Структурирование информации
29. Принципы структурирования информации
30. Методы структурирования информации.
31. Общие представления об элементах формальной логики.
32. Логические высказывания и их использование в задачах.
33. Понятие и структура комплекса технических средств.
34. Виды и параметры персональных компьютеров.
35. Основные составляющие архитектуры ПК: характеристика, параметры.
36. Понятие об автоматизированном рабочем месте.
37. Виды и классификация программного обеспечения.
38. Классификация, виды, области применения прикладного программного обеспечения.
39. Операционная система – классификация, функции, виды, особенности.
40. Офисные приложения: виды, назначение, особенности, использование.
ВОПРОСЫ К ЭКЗАМЕНУ
ПО ДИСЦИПЛИНЕ «ЭММ».
1. Модель задачи линейного программирования. Формы ее записи.
2. Дать определение следующих понятий: план, допустимый план, оптимальный план.
3. Построение исходного опорного плана.
4. Геометрическая интерпретация системы ограничений и целевой функции задачи линейного программирования.
5. Критерии оптимальности допустимого плана, применяемого в симплекс-методе.
6. Алгоритм симплексного метода решения задач линейного программирования.
7. Алгоритм определения разрешающего элемента симплекс-таблицы.
8. Признак неограниченности целевой функции в задаче линейного программирования. Геометрическая интерпретация.
9. М-метод (метод искусственного базиса).
10. Определение двойственной задачи линейного программирования. Понятие симметричной и несимметричной задачи.
11. Понятие двойственных задач. Свойства пары двойственных задач.
12. Экономическая интерпретация переменных прямой и двойственной задач.
13. Первая теорема двойственности.
14. Вторая теорема двойственности.
15. Методы построения опорного плана транспортной задачи (метод северо-западного угла, минимальной стоимости, двойного предпочтения).
16. Невырожденный опорный план транспортной задачи.
17. Транспортная задача открытого и закрытого типов.
18. Критерий оптимальности опорного плана транспортной задачи.
19. Метод потенциалов решения транспортной задачи. Признак оптимальности.
20. Построение цикла перераспределения перевозок метода потенциалов.
21. Ограничения по пропускной способности в транспортной задаче.
22. Переход к новому опорному плану транспортной задачи.
23. Графический метод решения нелинейных задач.
24. Решение задач дробно-линейного программирования.
25. Метод Гомори решения целочисленных задач.
26. Построение дополнительного ограничения по методу Гомори.
27. Задачи дискретного программирования.
28. Метод Лагранжа решения задач нелинейного программирования.
29. Основные понятия теории игр. Стратегия и ход игры. Классификация игр.
30. Игра с седловой точкой. Алгоритм проверки платежной матрицы на наличие седловой точки.
31. Понятие дублирующих и доминирующих стратегий. Способы сокращений размерности платежной матрицы.
32. Аналитическое решение игры с платежной матрицей 2х2. Теорема о размере выигрыша в игре со смешанными стратегиями.
33. Графическое решение игры с матрицей 2х2.
34. Приведение матричной игры к задаче линейного программирования.
35. Типы задач нелинейного программирования.
36. Пример экономической модели задачи нелинейного программирования.
37. Экономические задачи, решаемые методами теории игр.
38. Понятие задач стохастического программирования.
39. Понятие задач динамического программирования.
40. Классификация информационных ситуаций. Какой принцип лежит в основе этой ситуации?
41. Поясните, почему возникает необходимость оценить риск в относительном выражении?
42. Почему возникает целесообразность использования такого показателя оценки риска, как семивариация? Приведите формулу для её вычисления?
43. Показатели риска, которые содержат субъективную составляющую.
44. Эконометрический анализ и его этапы.
45. Простая линейная регрессионная модель.
46. Оценка параметров ПЛРМ (простой линейной регрессионной модели) по методу наименьших квадратов.
47. Проверка модели на адекватность опытным данным.
48. Нелинейные модели в эконометрии.
49. Многофакторные модели в эконометрии.
50. Понятие мультиколлинеарности.
51. Коэффициент парной корреляции, его свойства.
52. Коэффициент детерминации, его свойства.
53. Оценка дисперсии ошибок однофакторной линейной выборочной модели.
54. Классы нелинейных моделей.
55. Регрессионный анализ в эконометрии.
56. Корреляционный анализ в эконометрии.
57. Общая линейная регрессионная модель.
58. Частная корреляция. Множественная корреляция.
59. Автокорреляция.
| <== предыдущая | | | следующая ==> |
| Метод расчета по рабочим местам и нормативам численности. | | | Тематика курсовых работ по дисциплине |
Date: 2016-11-17; view: 479; Нарушение авторских прав