
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Связь ускорения со смещением
|
|
Величина  - максимальное ускорение (амплитуда колебаний ускорения). Следовательно, для ускорения имеем:
- максимальное ускорение (амплитуда колебаний ускорения). Следовательно, для ускорения имеем:  ,
а для случая нулевой начальной фазы: ,
а для случая нулевой начальной фазы: 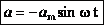 (см. график). (см. график).
| 
|
| Из анализа процесса колебательного движения, графиков и соответствующих математических выражений видно, что при прохождении колеблющимся телом положения равновесия (смещение равно нулю) ускорение равно нулю, а скорость тела максимальна (тело проходит положение равновесия по инерции), а при достижении амплитудного значения смещения – скорость равна нулю, а ускорение максимально по модулю (тело меняет направление своего движения). | |
Сравним выражения для смещения и ускорения при гармонических колебаниях:
 и и  . .
| |
Можно записать:  -
т.е. вторая производная смещения прямо пропорциональна (с противоположным знаком) смещению. Такое уравнение наз. уравнением гармонического колебания. Эта зависимость выполняется для любого гармонического колебания, независимо от его природы. Поскольку мы нигде не использовали параметров конкретной колебательной системы, то от них может зависеть только циклическая частота. -
т.е. вторая производная смещения прямо пропорциональна (с противоположным знаком) смещению. Такое уравнение наз. уравнением гармонического колебания. Эта зависимость выполняется для любого гармонического колебания, независимо от его природы. Поскольку мы нигде не использовали параметров конкретной колебательной системы, то от них может зависеть только циклическая частота.
|
3.2 Представление гармонических колебаний в виде вращающегося вектора. Сложение двух гармонических колебаний с одинаковыми частотами, совершающихся в одном направлении. Условия усиления и максимального усиления колебаний. Условия ослабления и наибольшего ослабления колебаний.
· Гармоническое (то есть синусоидальное) колебание может быть представлено графически в виде проекции на некоторую ось (обычно берут ось координат Оx) вектора, вращающегося с постоянной угловой скоростью ω. Длина вектора соответствуетамплитуде, угол поворота относительно оси (Ox) - фазе.
Сумма (или разность) двух и более колебаний на векторной диаграмме представлена при этом (геометрической) суммой[1] (или разностью) векторов этих колебаний. Мгновенное значение искомой величины определяется при этом проекцией вектора суммы на ось Оx, амплитуда - длиной этого вектора, а фаза - углом его поворота относительно Ox.
- Колеблющееся тело может принимать участие в нескольких колебательных процессах, тогда следует найти результирующее колебание, другими словами, колебания необходимо сложить. В данном разделе будем складывать гармонические колебания одного направления и одинаковой частоты

применяя метод вращающегося вектора амплитуды, построим графически векторные диаграммы этих колебаний (рис. 1). Tax как векторы A1 и A2 вращаются с одинаковой угловой скоростью ω0, то разность фаз (φ2 - φ1) между ними будет оставаться постоянной. Значит, уравнение результирующего колебания будет
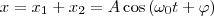 (1)
(1)
В формуле (1) амплитуда А и начальная фаза φ соответственно определяются выражениями
 (2)
(2)

Значит, тело, участвуя в двух гармонических колебаниях одного направления и одинаковой частоты, совершает при этом также гармоническое колебание в том же направлении и с той же частотой, что и складываемые колебания. Амплитуда результирующего колебания зависит от разности фаз (φ2 - φ1) складываемых колебаний.
3.3 Квазиупругая сила. Математический и физический маятники. Циклическая частота гармонического осциллятора. Энергия колебаний.
· 
Такая зависимость силы от смещения характерна для упругой силы силы. Поэтому силы иной физической природы удовлетворяющие тому же виду зависимости, называются квазиупругими.
· Математи́ческий ма́ятник — осциллятор, представляющий собой механическую систему, состоящую из материальной точки, находящейся на невесомой нерастяжимой нити или на невесомом стержне в однородном поле сил тяготения. Период малых собственных колебаний математического маятника длины l неподвижно подвешенного в однородном поле тяжести с ускорением свободного падения g равен
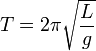
и не зависит[1] от амплитуды и массы маятника.
Физический маятник — осциллятор, представляющий собой твёрдое тело, совершающее колебания в поле каких-либо силотносительно точки, не являющейся центром масс этого тела, или неподвижной оси, перпендикулярной направлению действия сил и не проходящей через центр масс этого тела.
Пренебрегая сопротивлением среды, дифференциальное уравнение колебаний физического маятника в поле силы тяжести записывается следующим образом:
 .
.
· гармонический осциллятор — это система, уравнение движения которой описывается дифференциальным уравнением 2 x + ω0 x = 0, ¨ (1) где x — величина, совершающая колебания, ω0 — циклическая частота.
· При механических колебаниях колеблющееся тело (или материальная точка) обладает кинетической и потенциальной энергией. Кинетическая энергия тела W:
· 
(Скорость тела v = ds/dt)
Для вычисления потенциальной энергии тела воспользуемся самой общей формулой, связывающей силу и потенциальную энергию тела в поле этой силы:

где U - потенциальная энергия, набираемая (или теряемая) телом, движущимся в силовом поле F от точки 0 (точки, в которой потенциальная энергия принимается равной 0) до точки х.
Для силы, линейно зависящей от смещения (как в случае наших механических маятников, такие силы носят общее название квазиупругих сил) мы имеем:
 ;
;  ;
;  .
.

Сравнивая формулы для кинетической и потенциальной энергии, можно сделать выводы:
1. Полная механическая энергия тела не изменяется при колебаниях: 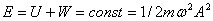
2. Частота колебаний кинетической и потенциальной энергии в 2 раза больше частоты колебаний маятника.
3. Колебания кинетической и потенциальной энергии сдвинуты друг относительно друга по фазе на p (на полпериода). Когда кинетическая энергия достигает максимума, потенциальная - минимума (нуля) и наоборот. Энергия при колебаниях постоянно перекачивается из потенциальной в кинетическую и обратно.
3.4 Упругие (механические) волны. Механизмы и условия возникновения упругих волн. Поперечные и продольные упругие волны, условия их возникновения. Формула скорости упругих волн в различных средах. Длина волны. Циклическое волновое число. Уравнение плоской волны.
Механической волной называется процесс распространения колебаний в упругой среде, который сопровождается передачей энергии от одной точки среды к другой.
Источником механической волны является колеблющее тело. Если источник колеблется синусоидально, то и волна в упругой среде будет иметь форму синусоиды. Колебания, вызванные в каком-либо месте упругой среды, распространяются в среде с определенной скоростью, зависящей от плотности и упругих свойств среды.
Подчеркнем, что при распространении волны отсутствует перенос вещества, т. е. частицы только колеблются вблизи положений равновесия.
Различают продольные и поперечные волны.
Упругая волна называется продольной, если частицы среды колеблются в направлении распространения волны. Продольные волны связаны с объемной деформацией упругой среды и потому могут распространяться в любой среде — твердой, жидкой и газообразной. Примером таких волн являются звуковые волны в воздухе.
Упругая волна называется поперечной, если частицы среды колеблются, оставаясь в плоскостях, перпендикулярных направлению распространения волны. Поперечные волны связаны с деформацией сдвига упругой среды и, следовательно, могут образовываться и распространяться только в средах, обладающих упругостью формы, т. е. в твердых телах. Примером поперечных волн могут, служить волны, распространяющиеся вдоль струн музыкальных инструментов.
Фазовая скорость различна для разных сред. В случае упругих поперечных волн (в твердом теле) фазовая скорость равна:
 ,где
,где  - модуль сдвига среды,
- модуль сдвига среды,  -ее плотность в невозбужденном состоянии (т.е. когда в этой среде не распространяется упругая волна).
-ее плотность в невозбужденном состоянии (т.е. когда в этой среде не распространяется упругая волна).
Фазовая скорость упругих продольных волн в твердом теле равна
 ,
,
где Е - модуль Юнга,  - плотность невозмущенной среды (твердого тела до момента распространения по нему волны).
- плотность невозмущенной среды (твердого тела до момента распространения по нему волны).
Фазовая скорость продольных волн в жидкости и газе определяется соотношением:
 ,где К – модуль объемной упругости среды – величина, характеризующая способность среды сопротивляться изменению ее объема,
,где К – модуль объемной упругости среды – величина, характеризующая способность среды сопротивляться изменению ее объема,  - плотность невозмущенной среды.
- плотность невозмущенной среды.
Фазовая скорость продольных волн в идеальном газе задается формулой:
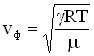
 - показатель адиабаты,
- показатель адиабаты,  - молярная масса, Т – абсолютная температура, R – универсальная газовая постоянная. Фазовая скорость в газе зависит от сорта газа (
- молярная масса, Т – абсолютная температура, R – универсальная газовая постоянная. Фазовая скорость в газе зависит от сорта газа ( ) и от его термодинамического состояния (Т).
) и от его термодинамического состояния (Т).
Длина́ волны́ — расстояние между двумя ближайшими друг к другу точками, колеблющимися в одинаковых фазах, обычно длина волны обозначается греческой буквой  . По аналогии с возникающими волнами в воде от брошенного в неё камня — расстояние между двумя соседними гребнями волны. Одна из основных характеристикколебаний. Измеряется в единицах расстояния (метры, сантиметры и т. п.). Величина
. По аналогии с возникающими волнами в воде от брошенного в неё камня — расстояние между двумя соседними гребнями волны. Одна из основных характеристикколебаний. Измеряется в единицах расстояния (метры, сантиметры и т. п.). Величина  , обратная длине волны, называется волновым числом и имеет смысл пространственной частоты.
, обратная длине волны, называется волновым числом и имеет смысл пространственной частоты.
Получить соотношение, связывающее длину волны с фазовой скоростью ( ) ичастотой(
) ичастотой(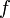 ) можно из определения. Длина волны соответствует пространственному периоду волны, то есть расстоянию, которое точка с постоянной фазой проходит за время, равное периоду колебаний
) можно из определения. Длина волны соответствует пространственному периоду волны, то есть расстоянию, которое точка с постоянной фазой проходит за время, равное периоду колебаний  , поэтому
, поэтому

Уравнение плоской волны:
Волна называется плоской, если ее волновые поверхности представляют совокупность плоскостей, параллельных друг другу. В плоской волне, распространяющейся вдоль оси ОХ, все величины s, характеризующие колебательные движение среды, зависят только от времени и координаты х точки М среды. Колебания происходят по закону s=f(t), но сдвинуты во времени на x\v. Поэтому ур-ие плоской волны имеет вид: s=f(t-x\v). Синусоидальная волна:
s=Asin(-t-wx\v+w0). A=const – амплитуда колебаний (амплит. волны). j=2w\T.
3.5 энергетические характеристики волн: объёмная плотность энергии волны, поток энергии волны, плотность потока энергии волны, интенсивность волны, спектральная плотность потока энергии излучения. Уровень интенсивности, уровень звукового давления, уровень громкости звука.
При волновом движении происходит перенос энергии, которая состоит из кинетической и потенциальной энергий колеблющихся частиц среды. Причем потенциальная энергия обусловлена деформацией вещества при взаимном смещении частиц. В отличие от колебаний свободного тела в волне не происходит взаимного перехода кинетической и потенциальной энергии частиц. Мгновенные значения той и другой энергии изменяются одновременно (в фазе) соответственно изменению смещения частиц.
Для мгновенного значения энергии (потенциальной и кинетической) одной частицы можно записать:
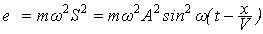 , (18)
, (18)
где S- смещение частицы, w- частота колебания частицы, A- амплитуда колебания частицы, V- скорость волнового процесса, в котором участвует частица, m – масса одной частицы.
Из формулы 18 следует, что мгновенные значения энергии каждой частицы среды изменяются во времени с удвоенной частотой колебания, причем в каждый момент времени эти значения для различных частиц отличаются. Однако среднее значение энергии за период колебания для всех частиц одинаково и составляет:
eср =  .
.
Рассчитаем энергию волны для некоторого объема DV среды, в которой она распространяется.

Если в единице объема среды содержится N частиц, то r = Nm —плотность среды и среднее значение энергии волны в объеме D V будет:
Еср =  (19)
(19)
где  — объемная плотность энергии волны.
— объемная плотность энергии волны.
Величина, численно равная средней энергии Еср, переносимой волной в единицу времени t через заданную поверхность S, перпендикулярную направлению распространения волны, называется потоком энергии через эту поверхность:
Ф =  (20)
(20)
и измеряется в единицах мощности - Вт.
Поток энергии, приходящийся на единицу поверхности, называется плотностью потока энергии:
 (21)
(21)
и измеряется в Вт/м2. Плотность потока энергии называют также интенсивностью волны.
В векторной форме:
 . (22)
. (22)
Плотность потока энергии, переносимого волной, можно рассматривать как вектор, совпадающий по направлению с вектором скорости волны.
Уровень интенсивности звука = 10 lg (J/J0) дБ
Поскольку звуки столь сильно различаются по интенсивности, удобнее рассматривать ее как логарифмическую величину и измерять в децибелах. Логарифмическая величина интенсивности представляет собой логарифм отношения рассматриваемого значения величины к ее значению, принимаемому за исходное. Уровень интенсивности J по отношению к некоторой условно выбранной интенсивности J0 равен
Таким образом, один звук, превышающий другой по уровню интенсивности на 20 дБ, превышает его в 100 раз по интенсивности.
В практике акустических измерений принято выражать интенсивность звука через соответствующую амплитуду избыточного давления Ре. Когда давление измеряется в децибелах относительно некоторого условно выбранного давления Р0, получают так называемый уровень звукового давления. Поскольку интенсивность звука пропорциональна величине Pe2, а lg(Pe2) = 2lgPe, уровень звукового давления определяется следующим образом:
Уровень звукового давления = 20 lg (Pe/P0) дБ
Условное давление Р0 = 2Ч10—5 Па соответствует стандартному порогу слышимости для звука с частотой 1 кГц.
Уровень громкости звука —относительная величина, которая выражается в фонах и численно равна уровню звукового давления (в децибелах — дБ), создаваемого синусоидальным тоном частотой 1 кГц такой же громкости, как и измеряемый звук (равногромким данному звуку).
3.6 Электромагнитная волна, условие и механизм ее возникновения. Скорость и длина электромагнитной волны в вакууме и в различных средах. Показатель преломления среды. Шкала электромагнитных волн. Характеристика электромагнитных волн различных интервалов длин волн.
Электромагнитные волны-это процесс распространения переменных магнитного и электрического полей. Переменное электрическое поле порождает магнитное, которое оказывается переменным. Оно порождает электрическое. Если возбудить с помощью колеблющихся зарядов переменное электромагнитное поле, то в окружающем заряды пространстве возникнет последовательность взаимных превращений электрического и магнитного полей, распространяющихся от точки к точке.
Скорость в вакууме: Е=М=1 V=C=3*10^8(м/с) V=C/((E*M)^1/2),
Где E-диэлектрическая проницаемость среды, M-магнитная проницаемость среды.
Показатель преломления(абс.)- отношение скорости волны в вакууме к скорости в среде.
n=C/V =лямда(0)/лямда лямда(0)=С/ню лямда=V/ню


3.7 Интерференция когерентных волн. Амплитуда результирующего колебания при интерференции 2х волн, условия максимумов и минимумов амплитуды. Интерференционный спектр.
Интерференция- такое положение когерентных волн, при которой имеет место перераспределение энергии волн в пространстве и устойчивое во времени и пространстве усиление колебаний в одних местах и ослабление в других.
Когерентные волны- волны одинаковой частоты, разность фаз которых не зависит от времени.

Если источник света монохромотичный (одного цвета)-то на интерференционной картине полосы черные и цвета соответствуют источнику. Если источник излучает белый (сложный) свет, то интерференционная картина представляет собой чередующиеся спектры цветов (от фиолетового до красного)=> максимумы разлагаются в спектры.
3.8. Осуществление интерференции света с помощью тонкой пленки. Интерференционные полосы равной толщины и равного наклона.
Кольца Ньютона (пример полос равной толщины) При отражении от соприкосновения плоскопараллельной толстой стеклянной пластины и плосковыпуклой линзы с большим радиусом кривизны. Радиус темных колец в отраженном и светлых в проходящем: r=(nRh)^1/2
Где h(лямда)-длина волны,R- радиус кривизны линзы.
Радиус светлых колец в отраженном и темных в проходящем:r=((n-1/2)Rh)^1/2


3.9. Стоячая волна как частный случай интерференции. Уравнение плоской стоячей волны. Амплитуда, узлы и пучности стоячей волны. Превращения энергии в стоячей волне. Образование стоячей волны в сплошной ограниченной среде. Условия возникновения волны в стержне, в столбе воздуха, в натянутой струне. Стоячая волна в сплошной ограниченной среде как резонансное колебание.



3.10. Дифракция волн. Объяснение дифракции волн на основе принципа Гюйгенса-Френеля. Дифракция Фраунгофера на одной щели и на дифракционной решетке. Дифракционный спектр.


4.1 Тепловое Излучение, его энергетические характеристики. Закон Кирхгофа, Стефана-Больцмана, Вина. Постулат Планка.
Тепловое излучение — электромагнитное излучение, испускаемое нагретыми телами за счёт их тепловой энергии.
Примером теплового излучения является свет от лампы накаливания.
Энергетические характеристики:
· Энергетическая светимость тела.
Энергетическая светимость тела- физическая величина, являющаяся функцией температуры и численно равная энергии, испускаемой телом в единицу времени с единицы площади поверхности по всем направлениям и по всему спектру частот.
Или (по лекции):
Это физическая величина, численно равная мощности излучения единицы поверхности нагретого тела по всему диапазону длин волн. 
 ,
,  Дж/с·м²=Вт/м²
Дж/с·м²=Вт/м²
· Спектральная плотность энергетической светимости.
Спектральная плотность энергетической светимости — функция частоты и температуры характеризующая распределение энергии излучения по всему спектру частот (или длин волн).
Или (по лекции):
Это физическая величина, численно равная энергии, излучаемой телом с единицы поверхности в единицу времени в единичном диапазоне длин волн.


· Поглощающая способность тела.
Поглощающая способность тела - функция частоты и температуры, показывающая, какая часть энергии электромагнитного излучения, падающего на тело, поглощается телом в области частот вблизи.

То, что не было в лекции:
· Отражающая способность тела.
Отражающая способность тела - функция частоты и температуры, показывающая какая часть энергии электромагнитного излучения, падающего на тело, отражается от него в области частот вблизи.
· Объемная плотность энергии излучения.
Объемная плотность энергии излучения - функция температуры, численно равная энергии электромагнитного излучения в единицу объема по всему спектру частот
· Спектральная плотность энергии.
Спектральная плотность энергии - функция частоты и температуры, связанная с объемной плотностью излучения формулой.
Закон излучения Кирхгофа — физический закон, установленный немецким физиком Кирхгофом в 1859 году. В современной формулировке закон звучит следующим образом:
Отношение излучательной способности любого тела к его поглощательной способности одинаково для всех тел при данной температуре для данной частоты и не зависит от их формы и химической природы.
Или (по лекции):
Для всех тел, нагретых до одинаковой температуры, отношение спектральная плотности энергетической светимости  к Поглощающей способности тела
к Поглощающей способности тела  есть величина постоянная.
есть величина постоянная.



Закон Стефана-Больцмана — закон излучения абсолютно чёрного тела. Определяет зависимость мощности излучения абсолютно чёрного тела от его температуры. Формулировка закона:
Мощность излучения абсолютно чёрного тела прямо пропорциональна четвёртой степени температуры тела.

 Дж·с−1·м−2 · К−4.
Дж·с−1·м−2 · К−4.
Закон смещения Вина даёт зависимость длины волны, на которой поток излучения энергии чёрного тела достигает своего максимума, от температуры чёрного тела.
Или (по лекции):

 обратно пропорциональна термодинамической температуре.
обратно пропорциональна термодинамической температуре.

Постулат Планка:
Тела излучают энергию не непрерывно, а порциями. Энергия такой порции(кванта) равна:
 h – постоянная Планка(6.63*10-34Дж*с),
h – постоянная Планка(6.63*10-34Дж*с),  - частота излучения
- частота излучения
4.2 Фотоэлектрический эффект. Вольт-амперная характеристика фототока. Опытные закономерности фотоэффекта. Уравнение Эйнштейна для фотоэффекта.
Фотоэффект - это испускание электронов веществом под действием света (и, вообще говоря, любого электромагнитного излучения).
Или (по лекции):
Явление вырывания электронов с поверхности металлов под действием света.
Вольт-амперная характеристика (ВАХ) — график зависимости тока от напряжения.

Опытные закономерности фотоэффекта или законы Столетова:
1) при неизменном спектральном составе электромагнитных излучений, падающих на фотокатод, фототок насыщения пропорционален энергетической освещенности катода.
Или по методичке:
Сила фототока насыщения Iн прямо пропорциональна световому потоку Ф – средней по времени энергии, подающей на поверхность катода за единицу времени.
 ,
,  - Коэффициент пропорциональности, называемый фоточувствительностью вещества.
- Коэффициент пропорциональности, называемый фоточувствительностью вещества.
Также:
 ,
,  - Количество электронов, покидающих катод за 1 секунду.
- Количество электронов, покидающих катод за 1 секунду.
2) Максимальная начальная скорость фотоэлектронов не зависит от интенсивности падающего света, а определяется только его частотой.
3) Для каждого вещества существует красная граница фотоэффекта, то есть минимальная частота ν0 света (зависящая от химической природы вещества и состояния поверхности), ниже которой фотоэффект невозможен.
Уравнение Эйнштейна для фотоэффекта.

Есть ещё много разновидностей этой формулы.
4.3 Фотоны. Корпускулярно-волновая природа света и частиц.
Фотоны.
Фотон (от др. греч. φῶς, род. Пад. φωτός, «свет») — элементарная частица, квант электромагнитного излучения (в узком смысле — света). Это безмассовая частица, способная существовать только двигаясь со скоростью света. Электрический заряд фотона также равен нулю.
Спин фотона равен 1 (частица является бозоном), но из-за нулевой массы покоя более подходящей характеристикой является спиральность, проекция спина частицы на направление движения. Фотон может находиться только в двух спиновых состояниях со спиральностью, равной. Этому свойству в классической электродинамике соответствует поперечность электромагнитной волны.
Корпускулярно-волновая природа света и частиц.
Корпускулярно-волновой дуализм — принцип, согласно которому любой объект может проявлять как волновые, так и корпускулярные свойства.
4.4 Ядерная модель атома.
Первая попытка создания модели атома на основе накопленных экспериментальных данных (1903 г.) принадлежит Дж. Томсону. Он считал, что атом представляет собой электронейтральную систему шарообразной формы радиусом, примерно равным 10–10 м. Положительный заряд атома равномерно распределен по всему объему шара, а отрицательно заряженные электроны находятся внутри него. Для объяснения линейчатых спектров испускания атомов Томсон пытался определить расположение электронов в атоме и рассчитать частоты их колебаний около положений равновесия. Однако эти попытки не увенчались успехом. Через несколько лет в опытах великого английского физика Э. Резерфорда было доказано, что модель Томсона неверна.

Первые прямые эксперименты по исследованию внутренней структуры атомов были выполнены Э. Резерфордом и его сотрудниками Э. Марсденом и Х. Гейгером в 1909–1911 годах. Резерфорд предложил применить зондирование атома с помощью α-частиц. От радиоактивного источника, заключенного в свинцовый контейнер, α-частицы направлялись на тонкую металлическую фольгу. Рассеянные частицы попадали на экран, покрытый слоем кристаллов сульфида цинка, способных светиться под ударами быстрых заряженных частиц. Сцинтилляции (вспышки) на экране наблюдались глазом с помощью микроскопа. Наблюдения рассеянных α-частиц в опыте Резерфорда можно было проводить под различными углами φ к первоначальному направлению пучка. Было обнаружено, что большинство α-частиц проходит через тонкий слой металла, практически не испытывая отклонения. Однако небольшая часть частиц отклоняется на значительные углы, превышающие 30°. Очень редкие α-частицы (приблизительно одна на десять тысяч) испытывали отклонение на углы, близкие к 180°.
Этот результат был совершенно неожиданным даже для Резерфорда. Его представления находил в резком противоречии с моделью атома Томсона, согласно которой положительный заряд распределен по всему объему атома. При таком распределении положительный заряд не может создать сильное электрическое поле, способное отбросить α-частицы назад. Электрическое поле однородного заряженного шара максимально на его поверхности и убывает до нуля по мере приближения к центру шара. Если бы радиус шара, в котором сосредоточен весь положительный заряд атома, уменьшился в n раз, то максимальная сила отталкивания, действующая на α-частицу, по закону Кулона возросла бы в n2 раз. Следовательно, при достаточно большом значении n α-частицы могли бы испытать рассеяние на большие углы вплоть до 180°. Эти соображения привели Резерфорда к выводу, что атом почти пустой, и весь его положительный заряд сосредоточен в малом объеме. Эту часть атома Резерфорд назвал атомным ядром. Так возникла ядерная модель атома.
Радикальные выводы о строении атома, следовавшие из опытов Резерфорда, заставляли многих ученых сомневаться в их справедливости. Опираясь на классические представления о движении микрочастиц, Резерфорд предложил планетарную модель атома. Согласно этой модели, в центре атома располагается положительно заряженное ядро, в котором сосредоточена почти вся масса атома. Атом в целом нейтрален. Вокруг ядра, подобно планетам, под действием кулоновских сил со стороны ядра вращаются электроны. Находиться в состоянии покоя электроны не могут, так как они упали бы на ядро.

Планетарная модель атома, предложенная Резерфордом, несомненно явилась крупным шагом вперед в развитии знаний о строении атома. Она была совершенно необходимой для объяснения опытов по рассеянию α-частиц, однако оказалась неспособной объяснить сам факт длительного существования атома, т. е. его устойчивость. По законам классической электродинамики, движущийся с ускорением заряд должен излучать электромагнитные волны, уносящие энергию. За короткое время (порядка 10–8 с) все электроны в атоме Резерфорда должны растратить всю свою энергию и упасть на ядро. То, что этого не происходит в устойчивых состояниях атома, показывает, что внутренние процессы в атоме не подчиняются классическим законам.
4.5 Состав ядер атомов. Радиоактивность ядер. Реакции деления и синтез ядер.
Состав ядер атомов.
Физики Д. Д. Иваненко и В. Гейзенберг в 1932 г. выдвинули протонно-нейтронную модель атомного ядра. Согласно этой модели, ядро атома любого вещества состоит из протонов и нейтронов. (Общее название протонов и нейтронов — нуклоны.) Число протонов равно заряду ядра и совпадает с номером элемента в таблице Менделеева. Сумма числа протонов и нейтронов равна массовому числу.
Химические вещества, занимающие одно и то же место в таблице Менделеева, но имеющие разную атомную массу, называются изотопами. Ядра изотопов отличаются числом нейтронов. Например, водород имеет три изотопа: протии — ядро состоит из одного протона, дейтерий — ядро состоит из одного протона и одного нейтрона, тритий — ядро состоит из одного протона и двух нейтронов.
Радиоактивность ядер.
Лишь небольшая часть нуклидов являются стабильными. В большинстве случаев ядерные силы оказываются неспособны обеспечить их постоянную целостность, и ядра рано или поздно распадаются. Это явление получило название радиоактивности.
Установлено, что радиоактивны все химические элементы с порядковым номером, большим 82.
α-распадом называют самопроизвольный распад атомного ядра на дочернее ядро и α-частицу (ядро атома 4He).
β-распад (точнее, бета-минус-распад, -распад) — это радиоактивный распад, сопровождающийся испусканием из ядра электрона и антинейтрино.
β-распад является внутринуклонным процессом. Он происходит вследствие превращения одного из d-кварков в одном из нейтронов ядра в u-кварк; при этом происходит превращение нейтрона в протон с испусканием электрона и антинейтрино:

Термин «гамма-распад» применяется редко; испускание ядром гамма-квантов называют обычно изомерным переходом. Гамма-излучение часто сопровождает другие типы распада.
Реакции деления и синтез ядер.
Деление представляет собой распад (расщепление) атомного ядра на две приближённо равные части (осколки), сопровождающийся выделением энергии и, в отд. случаях, испусканием одной или нескольких частиц, например, нейтронов. Некоторые тяжелые ядра могут делиться самопроизвольно (спонтанно), более легкие - в случае соударения с другими ядрами, обладающими большой энергией. Кроме того, тяжелые ядра, например, атомов урана, способны делиться под воздействием бомбардировки нейтронами, а поскольку при этом испускаются новые нейтроны, процесс может стать самоподдерживающимся, т.е. возникает цепная реакция. В ходе такой реакции деления происходит высвобождение большого количества энергии. Синтезом называется слияние ядер двух легких атомов с образованием нового ядра, соответствующего более тяжелому атому. Если это новое ядро стабильно, то при синтезе выделяется энергия, поскольку связи в нем оказываются более прочными, чем в исходных ядрах. От химических реакций ядерный синтез отличается участием в нем не только электронов атомов, но и их ядер. энергии, чем в реакциях деления. Синтез ядер идет в центр, области Солнца и других звезд, являясь источником их энергии.
4.6 Элементарные и фундаментальные частицы. Обменный механизм взаимодействия.
Элементарная частица — собирательный термин, относящийся к микрообъектам в субъядерном масштабе, которые невозможно расщепить на составные части.
Следует иметь в виду, что некоторые элементарные частицы (электрон, фотон, кварки и т. д.) на данный момент считаются бесструктурными и рассматриваются как первичные фундаментальные частицы.
Строение и поведение элементарных частиц изучается физикой элементарных частиц.
Все элементарные частицы делятся на два класса:
· бозоны — частицы с целым спином (например, фотон, глюон, мезоны).
· фермионы — частицы с полуцелым спином (например, электрон, протон, нейтрон, нейтрино).
Составные частицы:
адроны — частицы, участвующие во всех видах фундаментальных взаимодействий. Они состоят из кварков и подразделяются, в свою очередь, на:
мезоны — адроны с целым спином, то есть являющиеся бозонами;
барионы — адроны с полуцелым спином, то есть фермионы. К ним, в частности, относятся частицы, составляющие ядро атома, — протон и нейтрон.
Фундаментальные (бесструктурные) частицы:
лептоны — фермионы, которые имеют вид точечных частиц (т. е. не состоящих ни из чего) вплоть до масштабов порядка 10−18 м. Не участвуют в сильных взаимодействиях. Участие в электромагнитных взаимодействиях экспериментально наблюдалось только для заряженных лептонов (электроны, мюоны, тау-лептоны) и не наблюдалось для нейтрино. Известны 6 типов лептонов.
кварки — дробнозаряженные частицы, входящие в состав адронов. В свободном состоянии не наблюдались (для объяснения отсутствия таких наблюдений предложен механизм конфайнмента). Как и лептоны, делятся на 6 типов и считаются бесструктурными, однако, в отличие от лептонов, участвуют в сильном взаимодействии.
калибровочные бозоны — частицы, посредством обмена которыми осуществляются взаимодействия:
фотон — частица, переносящая электромагнитное взаимодействие;
восемь глюонов — частиц, переносящих сильное взаимодействие;
три промежуточных векторных бозона W+, W− и Z0, переносящие слабое взаимодействие;
гравитон — гипотетическая частица, переносящая гравитационное взаимодействие. Существование гравитонов, хотя пока не доказано экспериментально в связи со слабостью гравитационного взаимодействия, считается вполне вероятным; однако гравитон не входит в Стандартную модель элементарных частиц.
Адроны и лептоны образуют вещество. Калибровочные бозоны — это кванты разных типов взаимодействий.
Фундаментальная частица — бесструктурная элементарная частица, которую до настоящего времени не удалось описать как составную. В настоящее время термин применяется преимущественно для лептонов и кварков (по 6 частиц каждого рода, вместе с античастицами, составляют набор из 24 фундаментальных частиц) в совокупности с калибровочными бозонами (частицами-переносчиками фундаментальных взаимодействий).
Обменный механизм взаимодействия.
4.7 Молекулярно-кинетические представления о строении вещества в различных агрегатных состояниях. Статический метод описания состояния и поведения системы многих частиц. Функция распределения частиц по состояниям.
Молекулярно-кинетическая теория строения вещества дает стройное объяснение существованию трех агрегатных состояний - твердого, жидкого и газообразного, а также перехода вещества из одного состояния в другое, основываясь на различных силах притяжения и отталкивания, действующих между молекулами.
Основное положение молекулярно-кинетической теории строения вещества, вытекающее из опытных фактов, заключается в том, что атомы и молекулы, из которых состоят все макроскопические тела, находятся в состоянии непрерывного хаотического теплового движения.
Статический метод описания систем большого числа частиц основан на большом многообразии законов природы, которые не проявляют себя при анализе поведения нескольких частиц (если частицы не являются квантовыми!), однако великолепно (с большой точностью!) работают, если число частиц велико. Для квантовых частиц статистический метод необходимо применять даже для изучения небольшого количества частиц. Статистический метод рассматривает параметры движения частиц(например, координата, направление и модуль скорости частицы) как случайные величины, оперирует с усредненными характеристиками системы частиц, с функциями распределения, с вероятностями обнаружения частицы в том или ином состоянии.
Функция распределения частиц по состояниям.
Основное понятие статистической физики; характеризует плотность вероятности распределения частиц статистической системы по фазовому пространству (т. е. по координатам (qi и импульсам pi) в классической статистической физике или вероятность распределения по квантовомеханическим состояниям в квантовой статистике.
В классической статистической физике Ф. р. f (p, q, t) определяет вероятность dω = f (p, q, t) dp dq обнаружить систему из N частиц в момент времени t в элементе фазового объёма dpdq = dp1dq1... dpN ×dqN вблизи точки p1, q1,..., pN, qn. Учитывая, что перестановка тождественных (одинаковых) частиц не меняет состояния, следует уменьшить фазовый объём в N! раз; кроме того, удобно перейти к безразмерному элементу (Базового объёма, заменив dpdq на dpdq/N! h3N, где Планка постоянная h определяет минимальный размер ячейки в фазовом пространстве.















Date: 2016-11-17; view: 335; Нарушение авторских прав